Deep Learning-based Algebraic Reynolds Stress Closures for RANS Simulations of Turbulent Flows

Turbulence is ubiquitous in engineering and science, yet direct simulation is prohibitively expensive. The Reynolds-averaged Navier-Stokes (RANS) equations provide savings exceeding ten orders of magnitude but introduce unclosed terms (the closure problem). Offline-trained machine-learning (ML) closures suffer distribution shift in predictive simulations, while ML methods that bypass the governing equations struggle to generalise from scarce high-fidelity data. We develop a physics-derived deep learning closure model for RANS, the Deep Algebraic Reynolds Stress Model (DARSM), which can be trained on small datasets and accurately generalise across Reynolds numbers, to unseen geometries, and to different flow regimes. A neural network maps flow invariants to empirical parameters in an implicit algebraic Reynolds stress equation, derived from the Reynolds stress transport equations under the weak-equilibrium assumption, imposing physics-based structure on the ML closure. End-to-end optimisation through the governing PDEs and the coupled implicit closure eliminates distribution shift, but both unrolled and implicit automatic differentiation fail on the stiff coupled solver. We derive adjoint equations that exploit the solver's implicit-explicit structure for efficient optimisation. On canonical square-duct and periodic-hill benchmarks, DARSM reduces average test velocity error over baseline RANS by $2$-$4\times$ across Reynolds number, geometries, and flow regimes, with peak case-level reductions of $12\times$. The model trained on attached, anisotropy-dominated flows (square duct) accurately generalises without retraining to separated flows (periodic hills), a regime change in the underlying physics. DARSM also outperforms five established ML methods: offline training, tensor-basis neural networks, field-inversion machine learning, DeepONets, and physics-informed neural networks.

Model synthesis and identifiability analysis of stiff chemical reaction systems with inVAErt networks

We consider the problem of learning data-driven replicas for stiff systems of ordinary differential equations arising in chemical kinetics that can be evaluated with high computational efficiency. We first focus on training emulators for families of reaction equations under varying reaction rates, using conditional residual networks or long-short term memory architectures. We then apply a recently proposed data-driven framework known as ``inVAErt networks'' to address the ill-posed inverse problem of inferring reaction rates, integration time, and possibly initial conditions from a target set of species concentrations - a problem that has received relatively little attention in the literature. The proposed approach is demonstrated on chemical systems with reversible and irreversible kinetics, spanning 2 to 20 differential equations, 3 to 20 chemical species, and 3 to 25 reaction rate parameters. Relative root mean squared errors produced by the proposed emulators range from $10^{-5}$ for lower-dimensional systems to $10^{-4}$ and $10^{-3}$ for an air pollution model and a hydrogen-air reaction system, respectively. Manifolds of non-identifiable reaction rates recovered by the proposed approach can be analytically verified for simple systems and are consistent with local identifiability analysis in higher dimensions.

Active Control of Turbulent Airfoil Flows Using Adjoint-based Deep Learning

We train active neural-network flow controllers using a deep learning PDE augmentation method to optimize lift-to-drag ratios in turbulent airfoil flows at Reynolds number $5\times10^4$ and Mach number 0.4. Direct numerical simulation and large eddy simulation are employed to model compressible, unconfined flow over two- and three-dimensional semi-infinite NACA 0012 airfoils at angles of attack $\alpha = 5^\circ$, $10^\circ$, and $15^\circ$. Control actions, implemented through a blowing/suction jet at a fixed location and geometry on the upper surface, are adaptively determined by a neural network that maps local pressure measurements to optimal jet total pressure, enabling a sensor-informed control policy that responds spatially and temporally to unsteady flow conditions. The sensitivities of the flow to the neural network parameters are computed using the adjoint Navier-Stokes equations, which we construct using automatic differentiation applied to the flow solver. The trained flow controllers significantly improve the lift-to-drag ratios and reduce flow separation for both two- and three-dimensional airfoil flows, especially at $\alpha = 5^\circ$ and $10^\circ$. The 2D-trained models remain effective when applied out-of-sample to 3D flows, which demonstrates the robustness of the adjoint-trained control approach. The 3D-trained models capture the flow dynamics even more effectively, which leads to better energy efficiency and comparable performance for both adaptive (neural network) and offline (simplified, constant-pressure) controllers. These results underscore the effectiveness of this learning-based approach in improving aerodynamic performance.

Sampling-based Distributed Training with Message Passing Neural Network

In this study, we introduce a domain-decomposition-based distributed training and inference approach for message-passing neural networks (MPNN). Our objective is to address the challenge of scaling edge-based graph neural networks as the number of nodes increases. Through our distributed training approach, coupled with Nystr\"om-approximation sampling techniques, we present a scalable graph neural network, referred to as DS-MPNN (D and S standing for distributed and sampled, respectively), capable of scaling up to $O(10^5)$ nodes. We validate our sampling and distributed training approach on two cases: (a) a Darcy flow dataset and (b) steady RANS simulations of 2-D airfoils, providing comparisons with both single-GPU implementation and node-based graph convolution networks (GCNs). The DS-MPNN model demonstrates comparable accuracy to single-GPU implementation, can accommodate a significantly larger number of nodes compared to the single-GPU variant (S-MPNN), and significantly outperforms the node-based GCN.

Dynamic Deep Learning LES Closures: Online Optimization With Embedded DNS

Deep learning (DL) has recently emerged as a candidate for closure modeling of large-eddy simulation (LES) of turbulent flows. High-fidelity training data is typically limited: it is computationally costly (or even impossible) to numerically generate at high Reynolds numbers, while experimental data is also expensive to produce and might only include sparse/aggregate flow measurements. Thus, only a relatively small number of geometries and physical regimes will realistically be included in any training dataset. Limited data can lead to overfitting and therefore inaccurate predictions for geometries and physical regimes that are different from the training cases. We develop a new online training method for deep learning closure models in LES which seeks to address this challenge. The deep learning closure model is dynamically trained during a large-eddy simulation (LES) calculation using embedded direct numerical simulation (DNS) data. That is, in a small subset of the domain, the flow is computed at DNS resolutions in concert with the LES prediction. The closure model then adjusts its approximation to the unclosed terms using data from the embedded DNS. Consequently, the closure model is trained on data from the exact geometry/physical regime of the prediction at hand. An online optimization algorithm is developed to dynamically train the deep learning closure model in the coupled, LES-embedded DNS calculation.

Deep Learning Closure Models for Large-Eddy Simulation of Flows around Bluff Bodies

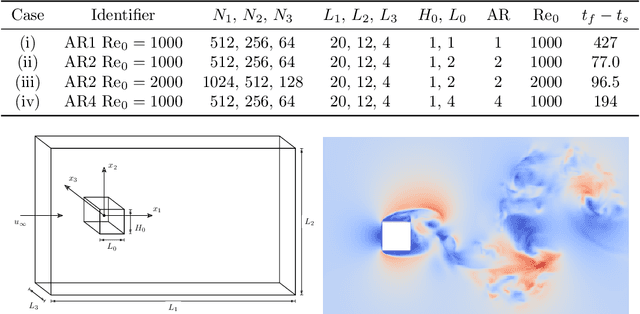
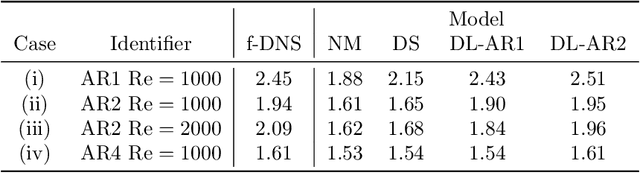
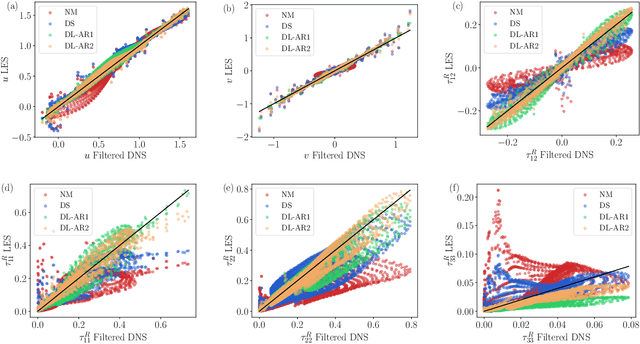
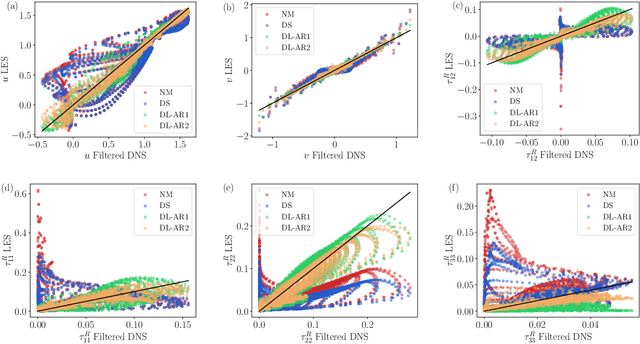
A deep learning (DL) closure model for large-eddy simulation (LES) is developed and evaluated for incompressible flows around a rectangular cylinder at moderate Reynolds numbers. Near-wall flow simulation remains a central challenge in aerodynamic modeling: RANS predictions of separated flows are often inaccurate, while LES can require prohibitively small near-wall mesh sizes. The DL-LES model is trained using adjoint PDE optimization methods to match, as closely as possible, direct numerical simulation (DNS) data. It is then evaluated out-of-sample (i.e., for new aspect ratios and Reynolds numbers not included in the training data) and compared against a standard LES model (the dynamic Smagorinsky model). The DL-LES model outperforms dynamic Smagorinsky and is able to achieve accurate LES predictions on a relatively coarse mesh (downsampled from the DNS grid by a factor of four in each Cartesian direction). We study the accuracy of the DL-LES model for predicting the drag coefficient, mean flow, and Reynolds stress. A crucial challenge is that the LES quantities of interest are the steady-state flow statistics; for example, the time-averaged mean velocity $\bar{u}(x) = \displaystyle \lim_{t \rightarrow \infty} \frac{1}{t} \int_0^t u(s,x) ds$. Calculating the steady-state flow statistics therefore requires simulating the DL-LES equations over a large number of flow times through the domain; it is a non-trivial question whether an unsteady partial differential equation model whose functional form is defined by a deep neural network can remain stable and accurate on $t \in [0, \infty)$. Our results demonstrate that the DL-LES model is accurate and stable over large physical time spans, enabling the estimation of the steady-state statistics for the velocity, fluctuations, and drag coefficient of turbulent flows around bluff bodies relevant to aerodynamic applications.

Embedded training of neural-network sub-grid-scale turbulence models

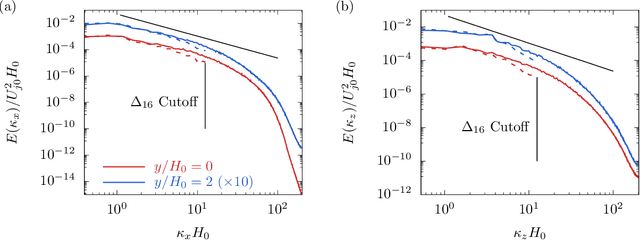
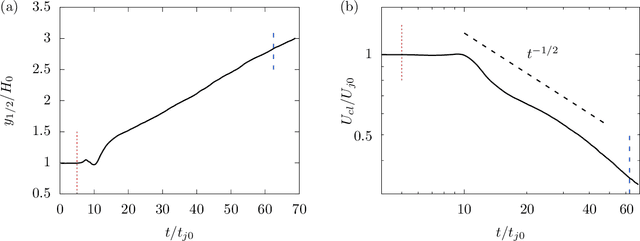
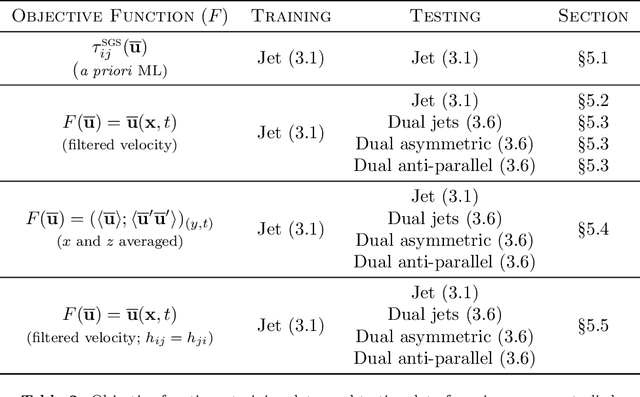
The weights of a deep neural network model are optimized in conjunction with the governing flow equations to provide a model for sub-grid-scale stresses in a temporally developing plane turbulent jet at Reynolds number $Re_0=6\,000$. The objective function for training is first based on the instantaneous filtered velocity fields from a corresponding direct numerical simulation, and the training is by a stochastic gradient descent method, which uses the adjoint Navier--Stokes equations to provide the end-to-end sensitivities of the model weights to the velocity fields. In-sample and out-of-sample testing on multiple dual-jet configurations show that its required mesh density in each coordinate direction for prediction of mean flow, Reynolds stresses, and spectra is half that needed by the dynamic Smagorinsky model for comparable accuracy. The same neural-network model trained directly to match filtered sub-grid-scale stresses -- without the constraint of being embedded within the flow equations during the training -- fails to provide a qualitatively correct prediction. The coupled formulation is generalized to train based only on mean-flow and Reynolds stresses, which are more readily available in experiments. The mean-flow training provides a robust model, which is important, though a somewhat less accurate prediction for the same coarse meshes, as might be anticipated due to the reduced information available for training in this case. The anticipated advantage of the formulation is that the inclusion of resolved physics in the training increases its capacity to extrapolate. This is assessed for the case of passive scalar transport, for which it outperforms established models due to improved mixing predictions.

DPM: A deep learning PDE augmentation method

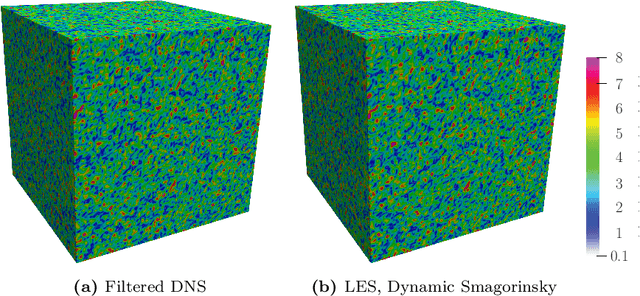
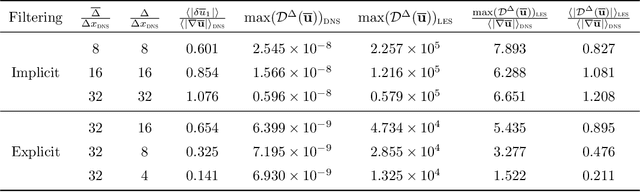
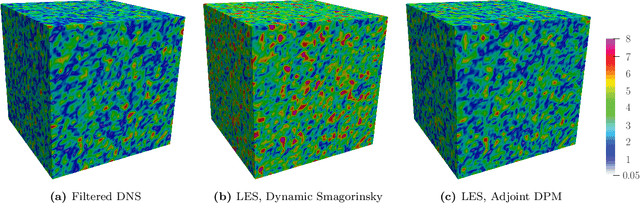
Machine learning for scientific applications faces the challenge of limited data. We propose a framework that leverages a priori known physics to reduce overfitting when training on relatively small datasets. A deep neural network is embedded in a partial differential equation (PDE) that expresses the known physics and learns to describe the corresponding unknown or unrepresented physics from the data. Crafted as such, the neural network can also provide corrections for erroneously represented physics, such as discretization errors associated with the PDE's numerical solution. Once trained, the deep learning PDE model (DPM) can make out-of-sample predictions for new physical parameters, geometries, and boundary conditions. Our approach optimizes over the functional form of the PDE. Estimating the embedded neural network requires optimizing over the entire PDE, which itself is a function of the neural network. Adjoint partial differential equations are used to efficiently calculate the high-dimensional gradient of the objective function with respect to the neural network parameters. A stochastic adjoint method (SAM), similar in spirit to stochastic gradient descent, further accelerates training. The approach is demonstrated and evaluated for turbulence predictions using large-eddy simulation (LES), a filtered version of the Navier--Stokes equation containing unclosed sub-filter-scale terms. The DPM outperforms the widely-used constant-coefficient and dynamic Smagorinsky models, even for filter sizes so large that these established models become qualitatively incorrect. It also significantly outperforms a priori trained models, which do not account for the full PDE. A relaxation of the discrete enforcement of the divergence-free constraint is also considered, instead allowing the DPM to approximately enforce incompressibility physics.