Deep Learning Closure Models for Large-Eddy Simulation of Flows around Bluff Bodies
Paper and Code
Aug 10, 2022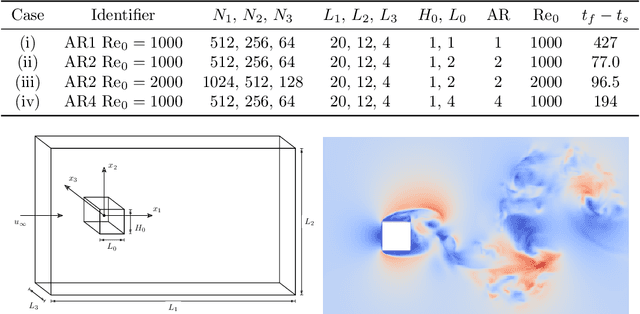
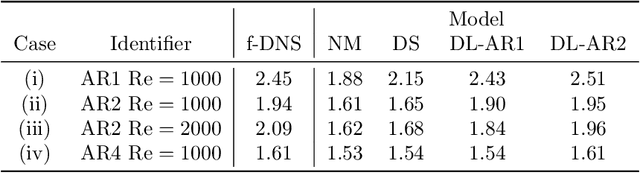
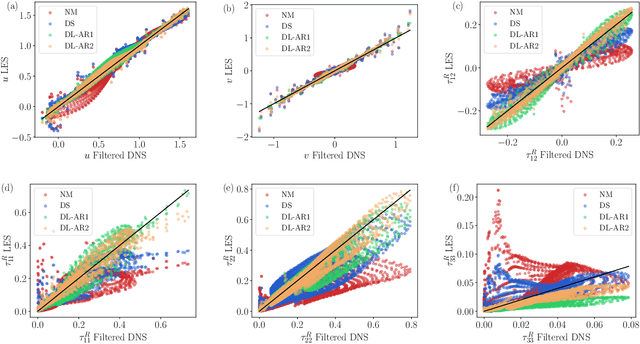
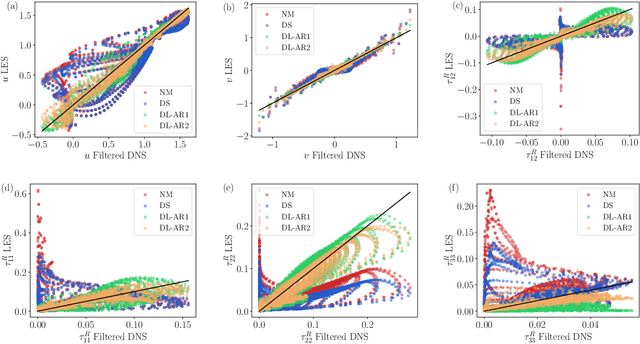
A deep learning (DL) closure model for large-eddy simulation (LES) is developed and evaluated for incompressible flows around a rectangular cylinder at moderate Reynolds numbers. Near-wall flow simulation remains a central challenge in aerodynamic modeling: RANS predictions of separated flows are often inaccurate, while LES can require prohibitively small near-wall mesh sizes. The DL-LES model is trained using adjoint PDE optimization methods to match, as closely as possible, direct numerical simulation (DNS) data. It is then evaluated out-of-sample (i.e., for new aspect ratios and Reynolds numbers not included in the training data) and compared against a standard LES model (the dynamic Smagorinsky model). The DL-LES model outperforms dynamic Smagorinsky and is able to achieve accurate LES predictions on a relatively coarse mesh (downsampled from the DNS grid by a factor of four in each Cartesian direction). We study the accuracy of the DL-LES model for predicting the drag coefficient, mean flow, and Reynolds stress. A crucial challenge is that the LES quantities of interest are the steady-state flow statistics; for example, the time-averaged mean velocity $\bar{u}(x) = \displaystyle \lim_{t \rightarrow \infty} \frac{1}{t} \int_0^t u(s,x) ds$. Calculating the steady-state flow statistics therefore requires simulating the DL-LES equations over a large number of flow times through the domain; it is a non-trivial question whether an unsteady partial differential equation model whose functional form is defined by a deep neural network can remain stable and accurate on $t \in [0, \infty)$. Our results demonstrate that the DL-LES model is accurate and stable over large physical time spans, enabling the estimation of the steady-state statistics for the velocity, fluctuations, and drag coefficient of turbulent flows around bluff bodies relevant to aerodynamic applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge