LieSolver: A PDE-constrained solver for IBVPs using Lie symmetries

We introduce a method for efficiently solving initial-boundary value problems (IBVPs) that uses Lie symmetries to enforce the associated partial differential equation (PDE) exactly by construction. By leveraging symmetry transformations, the model inherently incorporates the physical laws and learns solutions from initial and boundary data. As a result, the loss directly measures the model's accuracy, leading to improved convergence. Moreover, for well-posed IBVPs, our method enables rigorous error estimation. The approach yields compact models, facilitating an efficient optimization. We implement LieSolver and demonstrate its application to linear homogeneous PDEs with a range of initial conditions, showing that it is faster and more accurate than physics-informed neural networks (PINNs). Overall, our method improves both computational efficiency and the reliability of predictions for PDE-constrained problems.

Machine learning on knowledge graphs for context-aware security monitoring

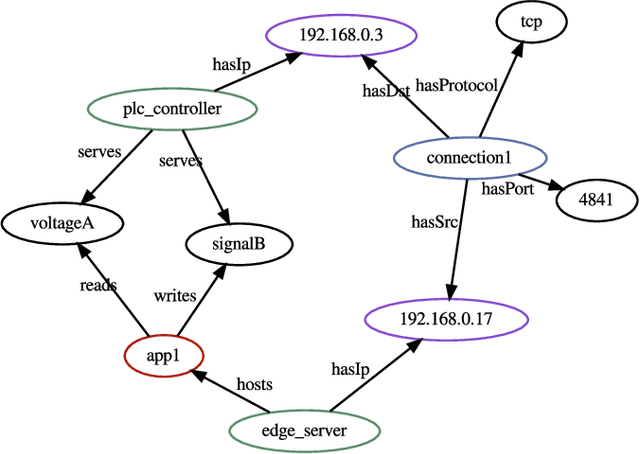
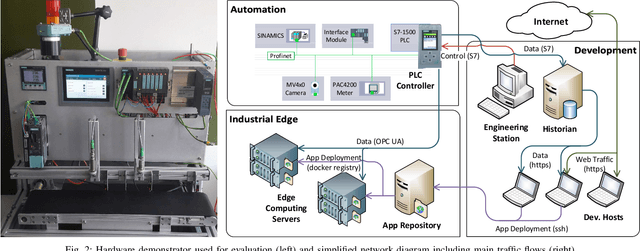
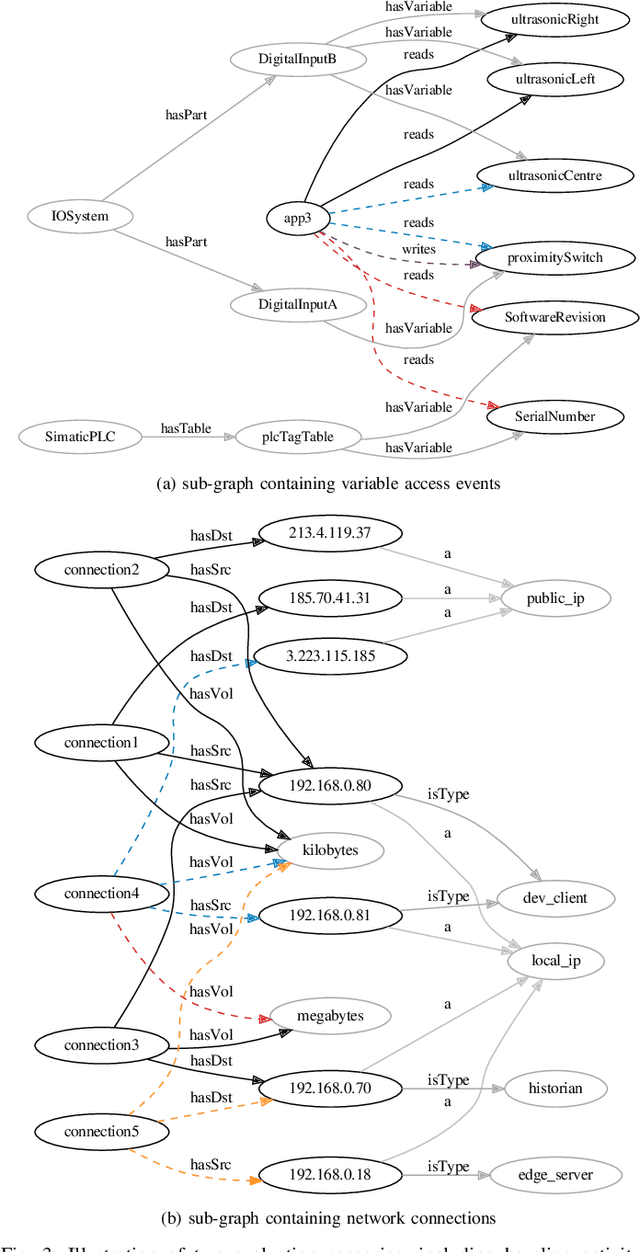
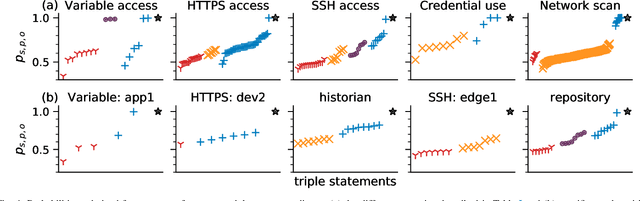
Machine learning techniques are gaining attention in the context of intrusion detection due to the increasing amounts of data generated by monitoring tools, as well as the sophistication displayed by attackers in hiding their activity. However, existing methods often exhibit important limitations in terms of the quantity and relevance of the generated alerts. Recently, knowledge graphs are finding application in the cybersecurity domain, showing the potential to alleviate some of these drawbacks thanks to their ability to seamlessly integrate data from multiple domains using human-understandable vocabularies. We discuss the application of machine learning on knowledge graphs for intrusion detection and experimentally evaluate a link-prediction method for scoring anomalous activity in industrial systems. After initial unsupervised training, the proposed method is shown to produce intuitively well-calibrated and interpretable alerts in a diverse range of scenarios, hinting at the potential benefits of relational machine learning on knowledge graphs for intrusion detection purposes.