Reinforcement learning to learn quantum states for Heisenberg scaling accuracy

Learning quantum states is a crucial task for realizing the potential of quantum information technology. Recently, neural approaches have emerged as promising methods for learning quantum states. We propose a meta-learning model that employs reinforcement learning (RL) to optimize the process of learning quantum states. For learning quantum states, our scheme trains a Hardware efficient ansatz with a blackbox optimization algorithm, called evolution strategy (ES). To enhance the efficiency of ES, a RL agent dynamically adjusts the hyperparameters of ES. To facilitate the RL training, we introduce an action repetition strategy inspired by curriculum learning. The RL agent significantly improves the sample efficiency of learning random quantum states, and achieves infidelity scaling close to the Heisenberg limit. We showcase that the RL agent trained using 3-qubit states can be generalized to learning up to 5-qubit states. These results highlight the utility of RL-driven meta-learning to enhance the efficiency and generalizability of learning quantum states. Our approach can be applicable to improve quantum control, quantum optimization, and quantum machine learning.

CAAP: Context-Aware Action Planning Prompting to Solve Computer Tasks with Front-End UI Only

Software robots have long been deployed in Robotic Process Automation (RPA) to automate mundane and repetitive computer tasks. The advent of Large Language Models (LLMs) with advanced reasoning capabilities has set the stage for these agents to now undertake more complex and even previously unseen tasks. However, the LLM-based automation techniques in recent literature frequently rely on HTML source codes for input, limiting their application to web environments. Moreover, the information contained in HTML codes is often inaccurate or incomplete, making the agent less reliable for practical applications. We propose an LLM-based agent that functions solely on the basis of screenshots for recognizing environments, while leveraging in-context learning to eliminate the need for collecting large datasets of human demonstration. Our strategy, named Context-Aware Action Planning (CAAP) prompting encourages the agent to meticulously review the context in various angles. Through our proposed methodology, we achieve a success rate of 94.4% on 67~types of MiniWoB++ problems, utilizing only 1.48~demonstrations per problem type. Our method offers the potential for broader applications, especially for tasks that require inter-application coordination on computers or smartphones, showcasing a significant advancement in the field of automation agents. Codes and models are accessible at https://github.com/caap-agent/caap-agent.

Simulation-guided Beam Search for Neural Combinatorial Optimization

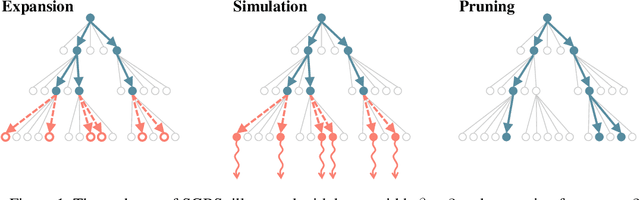
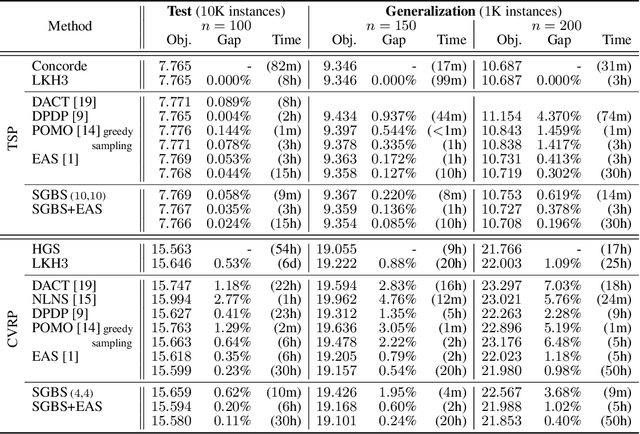
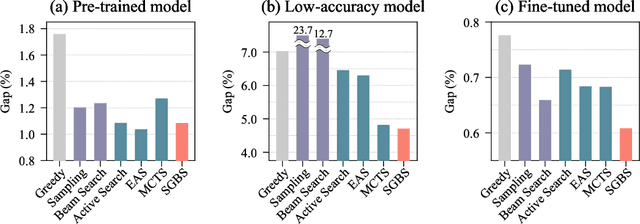
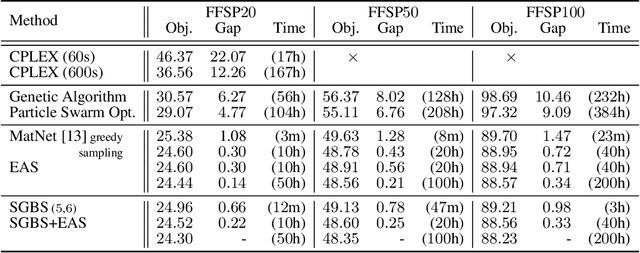
Neural approaches for combinatorial optimization (CO) equip a learning mechanism to discover powerful heuristics for solving complex real-world problems. While neural approaches capable of high-quality solutions in a single shot are emerging, state-of-the-art approaches are often unable to take full advantage of the solving time available to them. In contrast, hand-crafted heuristics perform highly effective search well and exploit the computation time given to them, but contain heuristics that are difficult to adapt to a dataset being solved. With the goal of providing a powerful search procedure to neural CO approaches, we propose simulation-guided beam search (SGBS), which examines candidate solutions within a fixed-width tree search that both a neural net-learned policy and a simulation (rollout) identify as promising. We further hybridize SGBS with efficient active search (EAS), where SGBS enhances the quality of solutions backpropagated in EAS, and EAS improves the quality of the policy used in SGBS. We evaluate our methods on well-known CO benchmarks and show that SGBS significantly improves the quality of the solutions found under reasonable runtime assumptions.

Matrix Encoding Networks for Neural Combinatorial Optimization

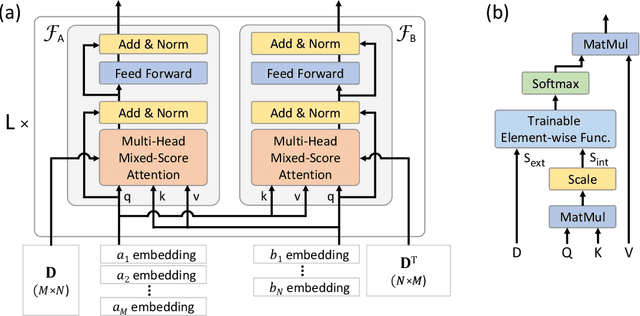
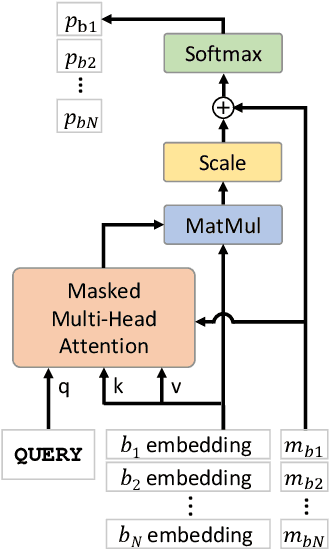
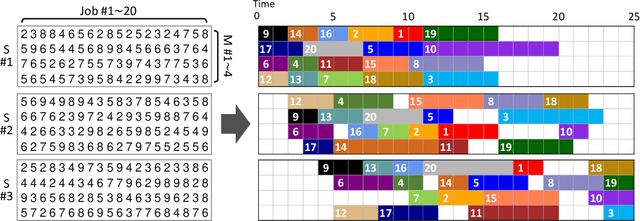
Machine Learning (ML) can help solve combinatorial optimization (CO) problems better. A popular approach is to use a neural net to compute on the parameters of a given CO problem and extract useful information that guides the search for good solutions. Many CO problems of practical importance can be specified in a matrix form of parameters quantifying the relationship between two groups of items. There is currently no neural net model, however, that takes in such matrix-style relationship data as an input. Consequently, these types of CO problems have been out of reach for ML engineers. In this paper, we introduce Matrix Encoding Network (MatNet) and show how conveniently it takes in and processes parameters of such complex CO problems. Using an end-to-end model based on MatNet, we solve asymmetric traveling salesman (ATSP) and flexible flow shop (FFSP) problems as the earliest neural approach. In particular, for a class of FFSP we have tested MatNet on, we demonstrate a far superior empirical performance to any methods (neural or not) known to date.

SelfMatch: Combining Contrastive Self-Supervision and Consistency for Semi-Supervised Learning

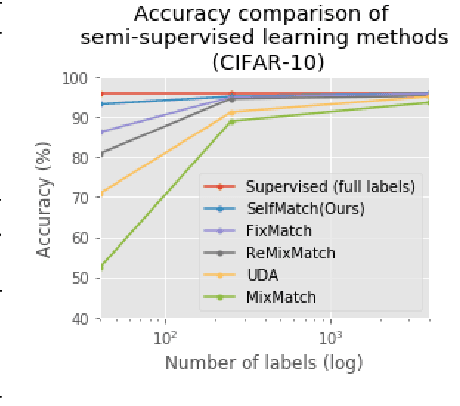
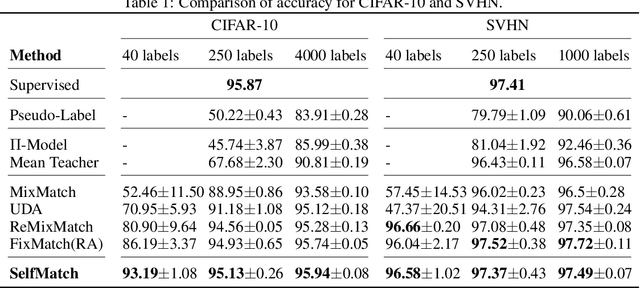
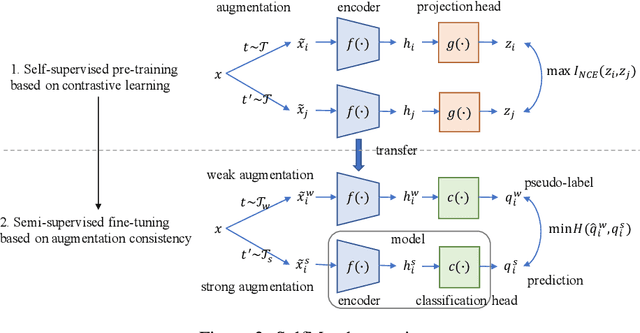
This paper introduces SelfMatch, a semi-supervised learning method that combines the power of contrastive self-supervised learning and consistency regularization. SelfMatch consists of two stages: (1) self-supervised pre-training based on contrastive learning and (2) semi-supervised fine-tuning based on augmentation consistency regularization. We empirically demonstrate that SelfMatch achieves the state-of-the-art results on standard benchmark datasets such as CIFAR-10 and SVHN. For example, for CIFAR-10 with 40 labeled examples, SelfMatch achieves 93.19% accuracy that outperforms the strong previous methods such as MixMatch (52.46%), UDA (70.95%), ReMixMatch (80.9%), and FixMatch (86.19%). We note that SelfMatch can close the gap between supervised learning (95.87%) and semi-supervised learning (93.19%) by using only a few labels for each class.

POMO: Policy Optimization with Multiple Optima for Reinforcement Learning

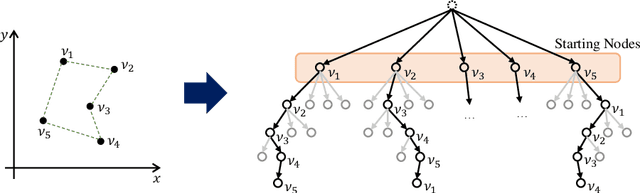
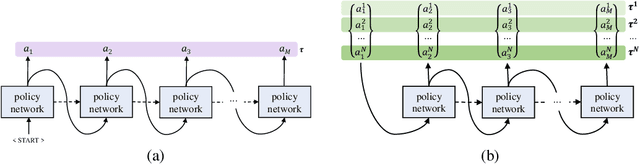
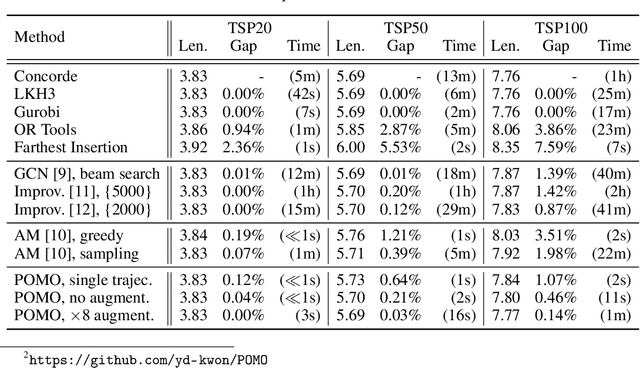
In neural combinatorial optimization (CO), reinforcement learning (RL) can turn a deep neural net into a fast, powerful heuristic solver of NP-hard problems. This approach has a great potential in practical applications because it allows near-optimal solutions to be found without expert guides armed with substantial domain knowledge. We introduce Policy Optimization with Multiple Optima (POMO), an end-to-end approach for building such a heuristic solver. POMO is applicable to a wide range of CO problems. It is designed to exploit the symmetries in the representation of a CO solution. POMO uses a modified REINFORCE algorithm that forces diverse rollouts towards all optimal solutions. Empirically, the low-variance baseline of POMO makes RL training fast and stable, and it is more resistant to local minima compared to previous approaches. We also introduce a new augmentation-based inference method, which accompanies POMO nicely. We demonstrate the effectiveness of POMO by solving three popular NP-hard problems, namely, traveling salesman (TSP), capacitated vehicle routing (CVRP), and 0-1 knapsack (KP). For all three, our solver based on POMO shows a significant improvement in performance over all recent learned heuristics. In particular, we achieve the optimality gap of 0.14% with TSP100 while reducing inference time by more than an order of magnitude.