Accelerating Large-Scale Regularized High-Order Tensor Recovery

Currently, existing tensor recovery methods fail to recognize the impact of tensor scale variations on their structural characteristics. Furthermore, existing studies face prohibitive computational costs when dealing with large-scale high-order tensor data. To alleviate these issue, assisted by the Krylov subspace iteration, block Lanczos bidiagonalization process, and random projection strategies, this article first devises two fast and accurate randomized algorithms for low-rank tensor approximation (LRTA) problem. Theoretical bounds on the accuracy of the approximation error estimate are established. Next, we develop a novel generalized nonconvex modeling framework tailored to large-scale tensor recovery, in which a new regularization paradigm is exploited to achieve insightful prior representation for large-scale tensors. On the basis of the above, we further investigate new unified nonconvex models and efficient optimization algorithms, respectively, for several typical high-order tensor recovery tasks in unquantized and quantized situations. To render the proposed algorithms practical and efficient for large-scale tensor data, the proposed randomized LRTA schemes are integrated into their central and time-intensive computations. Finally, we conduct extensive experiments on various large-scale tensors, whose results demonstrate the practicability, effectiveness and superiority of the proposed method in comparison with some state-of-the-art approaches.

Tensor Restricted Isometry Property Analysis For a Large Class of Random Measurement Ensembles

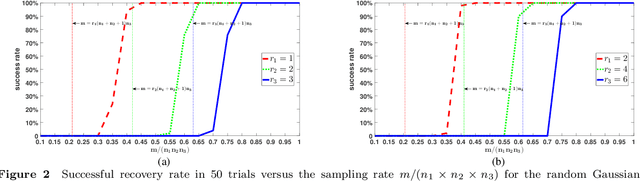
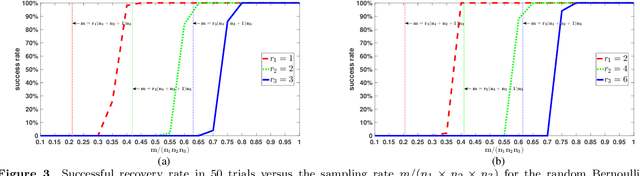
In previous work, theoretical analysis based on the tensor Restricted Isometry Property (t-RIP) established the robust recovery guarantees of a low-tubal-rank tensor. The obtained sufficient conditions depend strongly on the assumption that the linear measurement maps satisfy the t-RIP. In this paper, by exploiting the probabilistic arguments, we prove that such linear measurement maps exist under suitable conditions on the number of measurements in terms of the tubal rank r and the size of third-order tensor n1, n2, n3. And the obtained minimal possible number of linear measurements is nearly optimal compared with the degrees of freedom of a tensor with tubal rank r. Specially, we consider a random sub-Gaussian distribution that includes Gaussian, Bernoulli and all bounded distributions and construct a large class of linear maps that satisfy a t-RIP with high probability. Moreover, the validity of the required number of measurements is verified by numerical experiments.