Private Edge Density Estimation for Random Graphs: Optimal, Efficient and Robust

We give the first polynomial-time, differentially node-private, and robust algorithm for estimating the edge density of Erd\H{o}s-R\'enyi random graphs and their generalization, inhomogeneous random graphs. We further prove information-theoretical lower bounds, showing that the error rate of our algorithm is optimal up to logarithmic factors. Previous algorithms incur either exponential running time or suboptimal error rates. Two key ingredients of our algorithm are (1) a new sum-of-squares algorithm for robust edge density estimation, and (2) the reduction from privacy to robustness based on sum-of-squares exponential mechanisms due to Hopkins et al. (STOC 2023).

Private graphon estimation via sum-of-squares

We develop the first pure node-differentially-private algorithms for learning stochastic block models and for graphon estimation with polynomial running time for any constant number of blocks. The statistical utility guarantees match those of the previous best information-theoretic (exponential-time) node-private mechanisms for these problems. The algorithm is based on an exponential mechanism for a score function defined in terms of a sum-of-squares relaxation whose level depends on the number of blocks. The key ingredients of our results are (1) a characterization of the distance between the block graphons in terms of a quadratic optimization over the polytope of doubly stochastic matrices, (2) a general sum-of-squares convergence result for polynomial optimization over arbitrary polytopes, and (3) a general approach to perform Lipschitz extensions of score functions as part of the sum-of-squares algorithmic paradigm.

Computational-Statistical Gaps for Improper Learning in Sparse Linear Regression

We study computational-statistical gaps for improper learning in sparse linear regression. More specifically, given $n$ samples from a $k$-sparse linear model in dimension $d$, we ask what is the minimum sample complexity to efficiently (in time polynomial in $d$, $k$, and $n$) find a potentially dense estimate for the regression vector that achieves non-trivial prediction error on the $n$ samples. Information-theoretically this can be achieved using $\Theta(k \log (d/k))$ samples. Yet, despite its prominence in the literature, there is no polynomial-time algorithm known to achieve the same guarantees using less than $\Theta(d)$ samples without additional restrictions on the model. Similarly, existing hardness results are either restricted to the proper setting, in which the estimate must be sparse as well, or only apply to specific algorithms. We give evidence that efficient algorithms for this task require at least (roughly) $\Omega(k^2)$ samples. In particular, we show that an improper learning algorithm for sparse linear regression can be used to solve sparse PCA problems (with a negative spike) in their Wishart form, in regimes in which efficient algorithms are widely believed to require at least $\Omega(k^2)$ samples. We complement our reduction with low-degree and statistical query lower bounds for the sparse PCA problems from which we reduce. Our hardness results apply to the (correlated) random design setting in which the covariates are drawn i.i.d. from a mean-zero Gaussian distribution with unknown covariance.

Reaching Kesten-Stigum Threshold in the Stochastic Block Model under Node Corruptions

We study robust community detection in the context of node-corrupted stochastic block model, where an adversary can arbitrarily modify all the edges incident to a fraction of the $n$ vertices. We present the first polynomial-time algorithm that achieves weak recovery at the Kesten-Stigum threshold even in the presence of a small constant fraction of corrupted nodes. Prior to this work, even state-of-the-art robust algorithms were known to break under such node corruption adversaries, when close to the Kesten-Stigum threshold. We further extend our techniques to the $Z_2$ synchronization problem, where our algorithm reaches the optimal recovery threshold in the presence of similar strong adversarial perturbations. The key ingredient of our algorithm is a novel identifiability proof that leverages the push-out effect of the Grothendieck norm of principal submatrices.

SQ Lower Bounds for Random Sparse Planted Vector Problem

Consider the setting where a $\rho$-sparse Rademacher vector is planted in a random $d$-dimensional subspace of $R^n$. A classical question is how to recover this planted vector given a random basis in this subspace. A recent result by [ZSWB21] showed that the Lattice basis reduction algorithm can recover the planted vector when $n\geq d+1$. Although the algorithm is not expected to tolerate inverse polynomial amount of noise, it is surprising because it was previously shown that recovery cannot be achieved by low degree polynomials when $n\ll \rho^2 d^{2}$ [MW21]. A natural question is whether we can derive an Statistical Query (SQ) lower bound matching the previous low degree lower bound in [MW21]. This will - imply that the SQ lower bound can be surpassed by lattice based algorithms; - predict the computational hardness when the planted vector is perturbed by inverse polynomial amount of noise. In this paper, we prove such an SQ lower bound. In particular, we show that super-polynomial number of VSTAT queries is needed to solve the easier statistical testing problem when $n\ll \rho^2 d^{2}$ and $\rho\gg \frac{1}{\sqrt{d}}$. The most notable technique we used to derive the SQ lower bound is the almost equivalence relationship between SQ lower bound and low degree lower bound [BBH+20, MW21].

Fast algorithm for overcomplete order-3 tensor decomposition

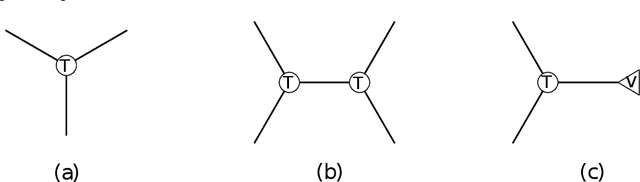
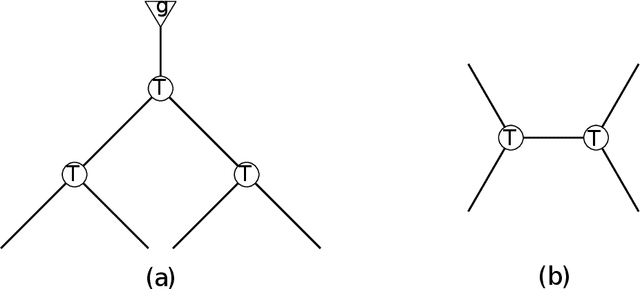
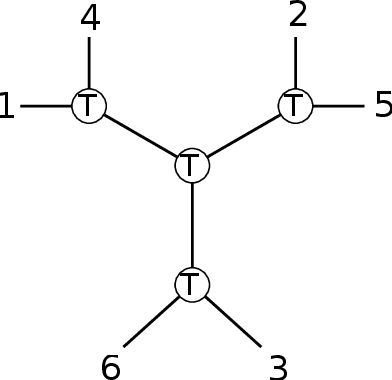
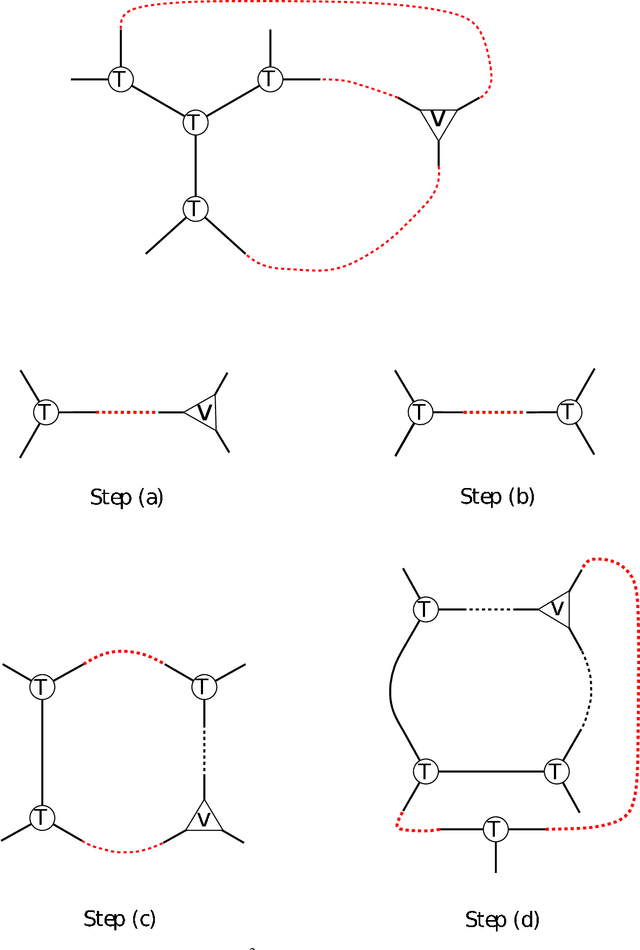
We develop the first fast spectral algorithm to decompose a random third-order tensor over R^d of rank up to O(d^{3/2}/polylog(d)). Our algorithm only involves simple linear algebra operations and can recover all components in time O(d^{6.05}) under the current matrix multiplication time. Prior to this work, comparable guarantees could only be achieved via sum-of-squares [Ma, Shi, Steurer 2016]. In contrast, fast algorithms [Hopkins, Schramm, Shi, Steurer 2016] could only decompose tensors of rank at most O(d^{4/3}/polylog(d)). Our algorithmic result rests on two key ingredients. A clean lifting of the third-order tensor to a sixth-order tensor, which can be expressed in the language of tensor networks. A careful decomposition of the tensor network into a sequence of rectangular matrix multiplications, which allows us to have a fast implementation of the algorithm.

Robust recovery for stochastic block models

We develop an efficient algorithm for weak recovery in a robust version of the stochastic block model. The algorithm matches the statistical guarantees of the best known algorithms for the vanilla version of the stochastic block model. In this sense, our results show that there is no price of robustness in the stochastic block model. Our work is heavily inspired by recent work of Banks, Mohanty, and Raghavendra (SODA 2021) that provided an efficient algorithm for the corresponding distinguishing problem. Our algorithm and its analysis significantly depart from previous ones for robust recovery. A key challenge is the peculiar optimization landscape underlying our algorithm: The planted partition may be far from optimal in the sense that completely unrelated solutions could achieve the same objective value. This phenomenon is related to the push-out effect at the BBP phase transition for PCA. To the best of our knowledge, our algorithm is the first to achieve robust recovery in the presence of such a push-out effect in a non-asymptotic setting. Our algorithm is an instantiation of a framework based on convex optimization (related to but distinct from sum-of-squares), which may be useful for other robust matrix estimation problems. A by-product of our analysis is a general technique that boosts the probability of success (over the randomness of the input) of an arbitrary robust weak-recovery algorithm from constant (or slowly vanishing) probability to exponentially high probability.

Estimating Rank-One Spikes from Heavy-Tailed Noise via Self-Avoiding Walks

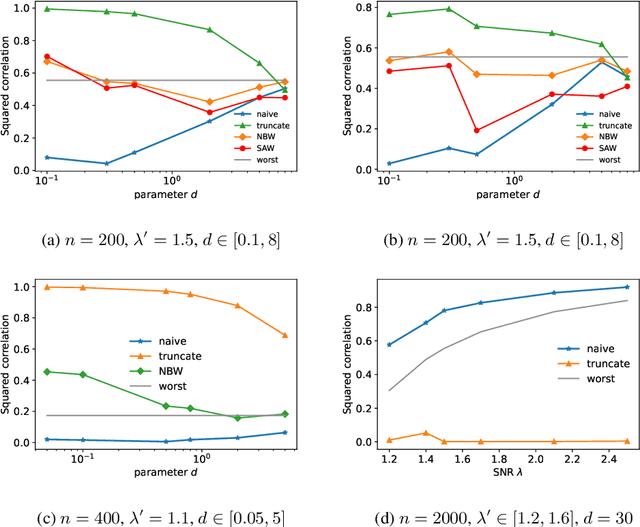
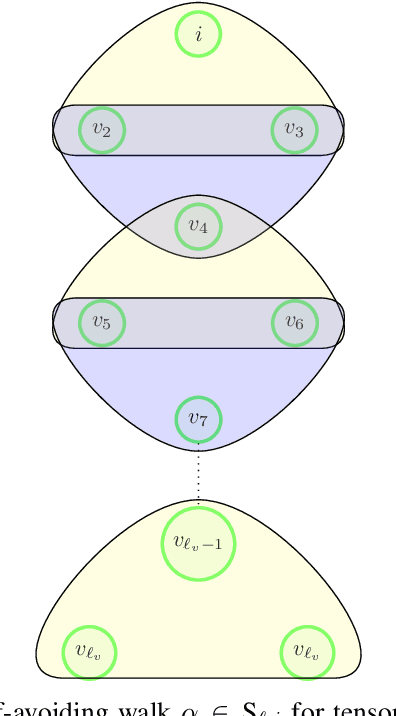
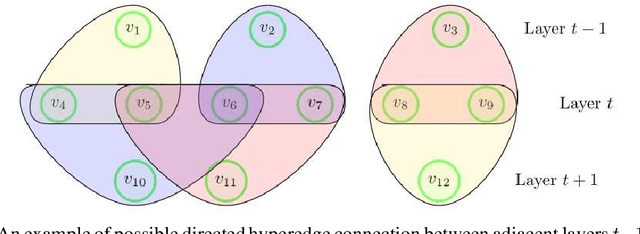
We study symmetric spiked matrix models with respect to a general class of noise distributions. Given a rank-1 deformation of a random noise matrix, whose entries are independently distributed with zero mean and unit variance, the goal is to estimate the rank-1 part. For the case of Gaussian noise, the top eigenvector of the given matrix is a widely-studied estimator known to achieve optimal statistical guarantees, e.g., in the sense of the celebrated BBP phase transition. However, this estimator can fail completely for heavy-tailed noise. In this work, we exhibit an estimator that works for heavy-tailed noise up to the BBP threshold that is optimal even for Gaussian noise. We give a non-asymptotic analysis of our estimator which relies only on the variance of each entry remaining constant as the size of the matrix grows: higher moments may grow arbitrarily fast or even fail to exist. Previously, it was only known how to achieve these guarantees if higher-order moments of the noises are bounded by a constant independent of the size of the matrix. Our estimator can be evaluated in polynomial time by counting self-avoiding walks via a color -coding technique. Moreover, we extend our estimator to spiked tensor models and establish analogous results.