Physics-informed Temporal Alignment for Auto-regressive PDE Foundation Models

Auto-regressive partial differential equation (PDE) foundation models have shown great potential in handling time-dependent data. However, these models suffer from the shortcut problem deeply rooted in auto-regressive prediction, causing error accumulation. The challenge becomes particularly evident for out-of-distribution data, as the pretraining performance may approach random model initialization for downstream tasks with long-term dynamics. To deal with this problem, we propose physics-informed temporal alignment (PITA), a self-supervised learning framework inspired by inverse problem solving. Specifically, PITA aligns the physical dynamics discovered at different time steps on each given PDE trajectory by integrating physics-informed constraints into the self-supervision signal. The alignment is derived from observation data without relying on known physics priors, indicating strong generalization ability to the out-of-distribution data. Extensive experiments show that PITA significantly enhances the accuracy and robustness of existing foundation models on diverse time-dependent PDE data. The code is available at https://github.com/SCAILab-USTC/PITA.

Residual-Quantile Adjustment for Adaptive Training of Physics-informed Neural Network

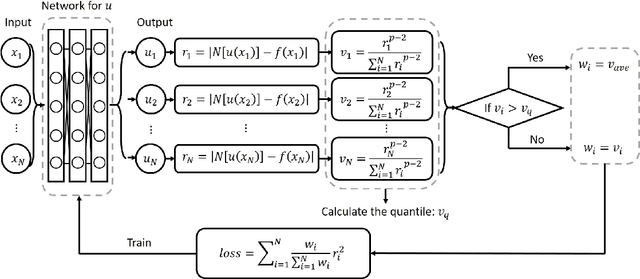
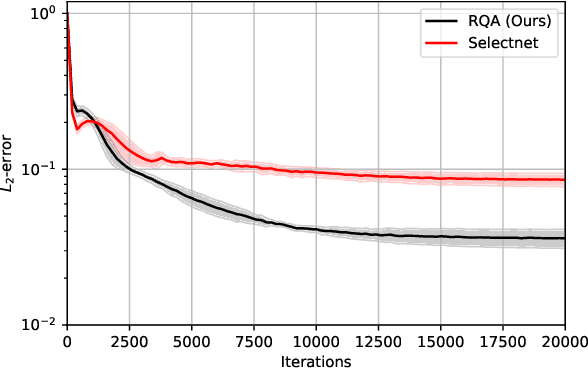
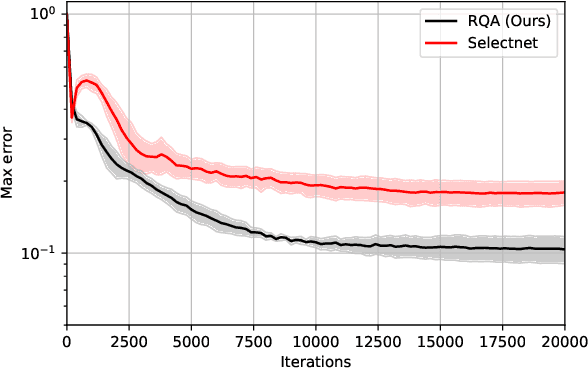
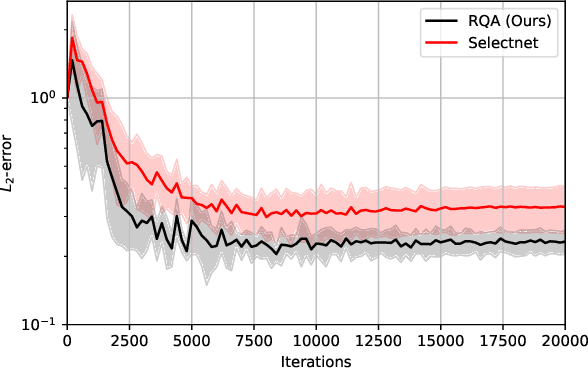
Adaptive training methods for physical-informed neural network (PINN) require dedicated constructions of the distribution of weights assigned at each training sample. To efficiently seek such an optimal weight distribution is not a simple task and most existing methods choose the adaptive weights based on approximating the full distribution or the maximum of residuals. In this paper, we show that the bottleneck in the adaptive choice of samples for training efficiency is the behavior of the tail distribution of the numerical residual. Thus, we propose the Residual-Quantile Adjustment (RQA) method for a better weight choice for each training sample. After initially setting the weights proportional to the $p$-th power of the residual, our RQA method reassign all weights above $q$-quantile ($90\%$ for example) to the median value, so that the weight follows a quantile-adjusted distribution derived from the residuals. With the iterative reweighting technique, RQA is also very easy to implement. Experiment results show that the proposed method can outperform several adaptive methods on various partial differential equation (PDE) problems.