Dialogues for proof search

Dialogue games are a two-player semantics for a variety of logics, including intuitionistic and classical logic. Dialogues can be viewed as a kind of analytic calculus not unlike tableaux. Can dialogue games be an effective foundation for proof search in intuitionistic logic (both first-order and propositional)? We announce Kuno, an automated theorem prover for intuitionistic first-order logic based on dialogue games.

Premise Selection for Mathematics by Corpus Analysis and Kernel Methods

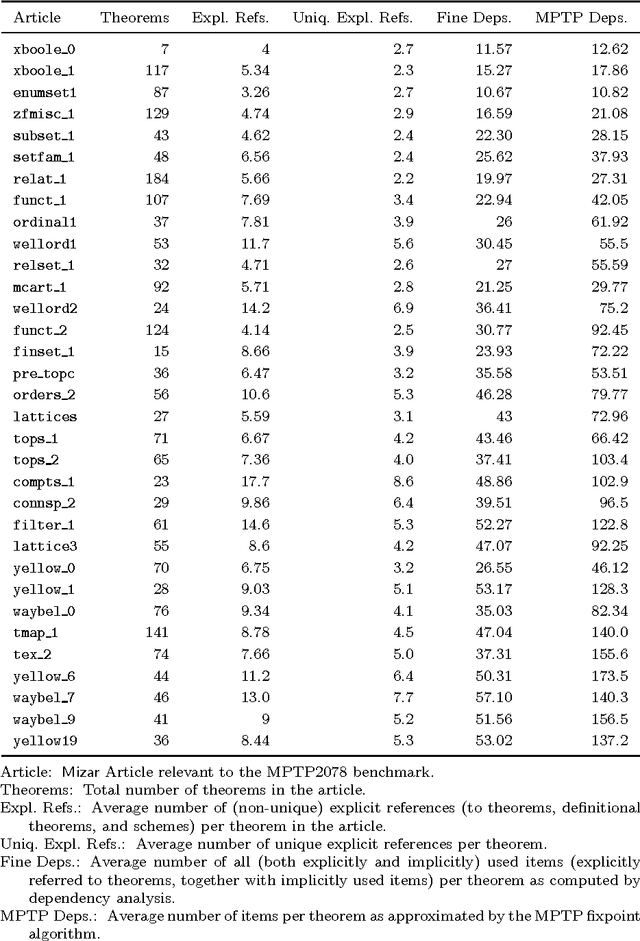
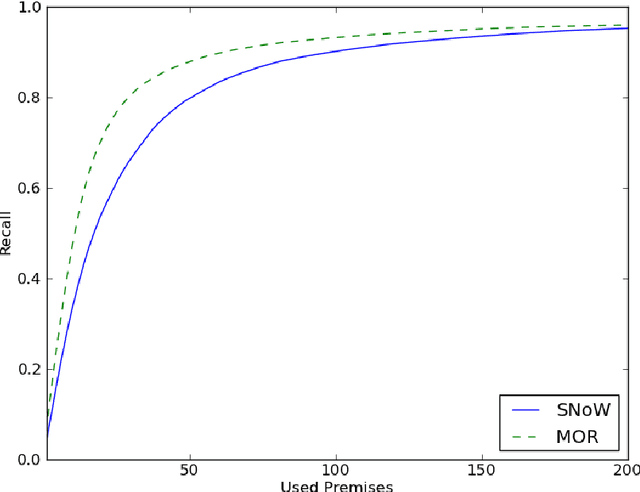
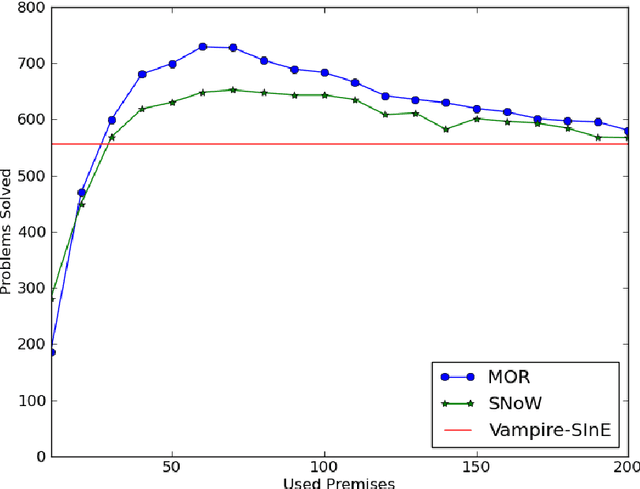
Smart premise selection is essential when using automated reasoning as a tool for large-theory formal proof development. A good method for premise selection in complex mathematical libraries is the application of machine learning to large corpora of proofs. This work develops learning-based premise selection in two ways. First, a newly available minimal dependency analysis of existing high-level formal mathematical proofs is used to build a large knowledge base of proof dependencies, providing precise data for ATP-based re-verification and for training premise selection algorithms. Second, a new machine learning algorithm for premise selection based on kernel methods is proposed and implemented. To evaluate the impact of both techniques, a benchmark consisting of 2078 large-theory mathematical problems is constructed,extending the older MPTP Challenge benchmark. The combined effect of the techniques results in a 50% improvement on the benchmark over the Vampire/SInE state-of-the-art system for automated reasoning in large theories.

Eliciting implicit assumptions of proofs in the MIZAR Mathematical Library by property omission

When formalizing proofs with interactive theorem provers, it often happens that extra background knowledge (declarative or procedural) about mathematical concepts is employed without the formalizer explicitly invoking it, to help the formalizer focus on the relevant details of the proof. In the contexts of producing and studying a formalized mathematical argument, such mechanisms are clearly valuable. But we may not always wish to suppress background knowledge. For certain purposes, it is important to know, as far as possible, precisely what background knowledge was implicitly employed in a formal proof. In this note we describe an experiment conducted on the MIZAR Mathematical Library of formal mathematical proofs to elicit one such class of implicitly employed background knowledge: properties of functions and relations (e.g., commutativity, asymmetry, etc.).