Formally-Sharp DAgger for MCTS: Lower-Latency Monte Carlo Tree Search using Data Aggregation with Formal Methods

We study how to efficiently combine formal methods, Monte Carlo Tree Search (MCTS), and deep learning in order to produce high-quality receding horizon policies in large Markov Decision processes (MDPs). In particular, we use model-checking techniques to guide the MCTS algorithm in order to generate offline samples of high-quality decisions on a representative set of states of the MDP. Those samples can then be used to train a neural network that imitates the policy used to generate them. This neural network can either be used as a guide on a lower-latency MCTS online search, or alternatively be used as a full-fledged policy when minimal latency is required. We use statistical model checking to detect when additional samples are needed and to focus those additional samples on configurations where the learnt neural network policy differs from the (computationally-expensive) offline policy. We illustrate the use of our method on MDPs that model the Frozen Lake and Pac-Man environments -- two popular benchmarks to evaluate reinforcement-learning algorithms.

Learning Probabilistic Temporal Safety Properties from Examples in Relational Domains

We propose a framework for learning a fragment of probabilistic computation tree logic (pCTL) formulae from a set of states that are labeled as safe or unsafe. We work in a relational setting and combine ideas from relational Markov Decision Processes with pCTL model-checking. More specifically, we assume that there is an unknown relational pCTL target formula that is satisfied by only safe states, and has a horizon of maximum $k$ steps and a threshold probability $\alpha$. The task then consists of learning this unknown formula from states that are labeled as safe or unsafe by a domain expert. We apply principles of relational learning to induce a pCTL formula that is satisfied by all safe states and none of the unsafe ones. This formula can then be used as a safety specification for this domain, so that the system can avoid getting into dangerous situations in future. Following relational learning principles, we introduce a candidate formula generation process, as well as a method for deciding which candidate formula is a satisfactory specification for the given labeled states. The cases where the expert knows and does not know the system policy are treated, however, much of the learning process is the same for both cases. We evaluate our approach on a synthetic relational domain.

Lifted Model Checking for Relational MDPs

Model checking has been developed for verifying the behaviour of systems with stochastic and non-deterministic behavior. It is used to provide guarantees about such systems. While most model checking methods focus on propositional models, various probabilistic planning and reinforcement frameworks deal with relational domains, for instance, STRIPS planning and relational Markov Decision Processes. Using propositional model checking in relational settings requires one to ground the model, which leads to the well known state explosion problem and intractability. We present pCTL-REBEL, a lifted model checking approach for verifying pCTL properties on relational MDPs. It extends REBEL, the relational Bellman update operator, which is a lifted value iteration approach for model-based relational reinforcement learning, toward relational model-checking. PCTL-REBEL is lifted, which means that rather than grounding, the model exploits symmetries and reasons at an abstract relational level. Theoretically, we show that the pCTL model checking approach is decidable for relational MDPs even for possibly infinite domains provided that the states have a bounded size. Practically, we contribute algorithms and an implementation of lifted relational model checking, and we show that the lifted approach improves the scalability of the model checking approach.

Active Learning of Sequential Transducers with Side Information about the Domain

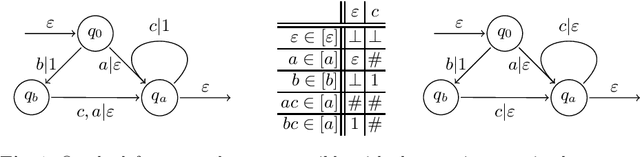
Active learning is a setting in which a student queries a teacher, through membership and equivalence queries, in order to learn a language. Performance on these algorithms is often measured in the number of queries required to learn a target, with an emphasis on costly equivalence queries. In graybox learning, the learning process is accelerated by foreknowledge of some information on the target. Here, we consider graybox active learning of subsequential string transducers, where a regular overapproximation of the domain is known by the student. We show that there exists an algorithm using string equation solvers that uses this knowledge to learn subsequential string transducers with a better guarantee on the required number of equivalence queries than classical active learning.

Online Learning of Non-Markovian Reward Models

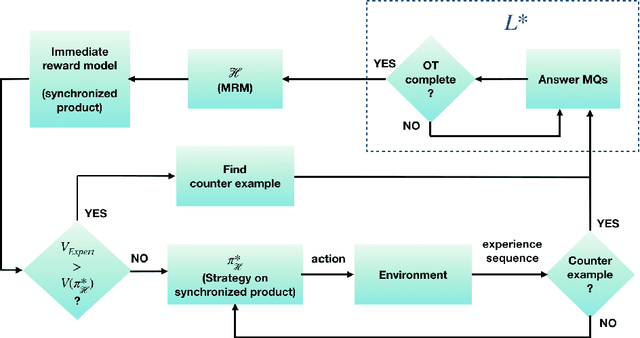
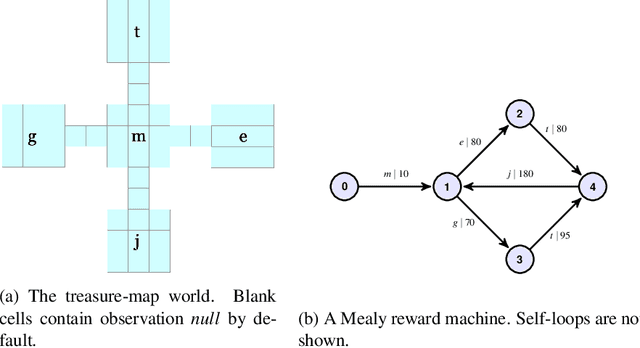
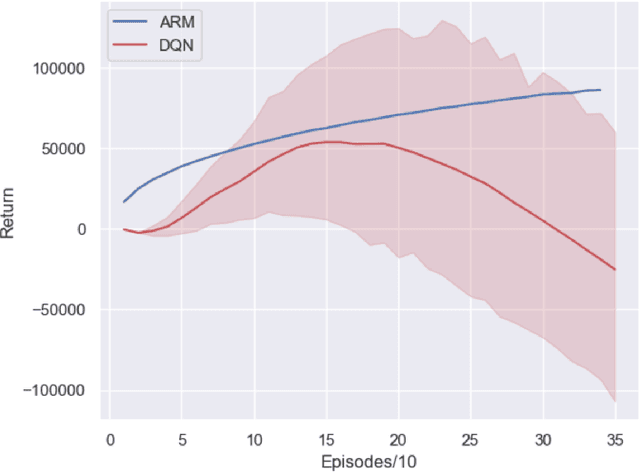
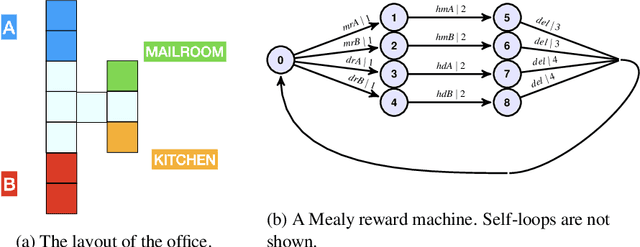
There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks, that is, rewards are non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine, a finite state automaton that produces output sequences from input sequences. In our formal setting, we consider a Markov decision process (MDP) that models the dynamics of the environment in which the agent evolves and a Mealy machine synchronized with this MDP to formalize the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown to the agent and must be learned. Our approach to overcome this challenge is to use Angluin's $L^*$ active learning algorithm to learn a Mealy machine representing the underlying non-Markovian reward machine (MRM). Formal methods are used to determine the optimal strategy for answering so-called membership queries posed by $L^*$. Moreover, we prove that the expected reward achieved will eventually be at least as much as a given, reasonable value provided by a domain expert. We evaluate our framework on three problems. The results show that using $L^*$ to learn an MRM in a non-Markovian reward decision process is effective.

Safe Learning for Near Optimal Scheduling

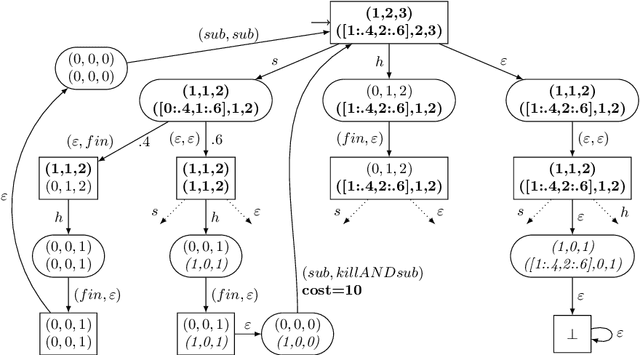
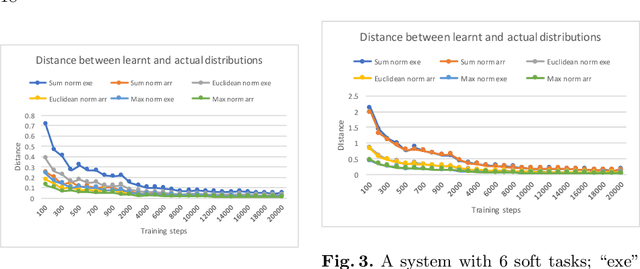
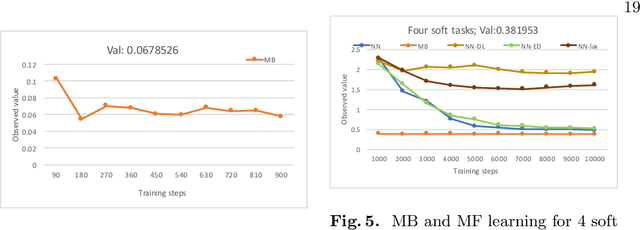
In this paper, we investigate the combination of synthesis techniques and learning techniques to obtain safe and near optimal schedulers for a preemptible task scheduling problem. We study both model-based learning techniques with PAC guarantees and model-free learning techniques based on shielded deep Q-learning. The new learning algorithms have been implemented to conduct experimental evaluations.

Mixing Probabilistic and non-Probabilistic Objectives in Markov Decision Processes

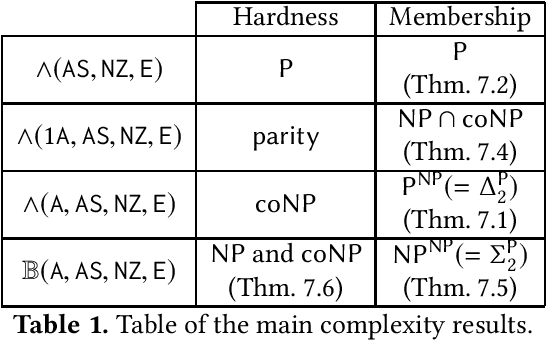
In this paper, we consider algorithms to decide the existence of strategies in MDPs for Boolean combinations of objectives. These objectives are omega-regular properties that need to be enforced either surely, almost surely, existentially, or with non-zero probability. In this setting, relevant strategies are randomized infinite memory strategies: both infinite memory and randomization may be needed to play optimally. We provide algorithms to solve the general case of Boolean combinations and we also investigate relevant subcases. We further report on complexity bounds for these problems.

Learning Non-Markovian Reward Models in MDPs

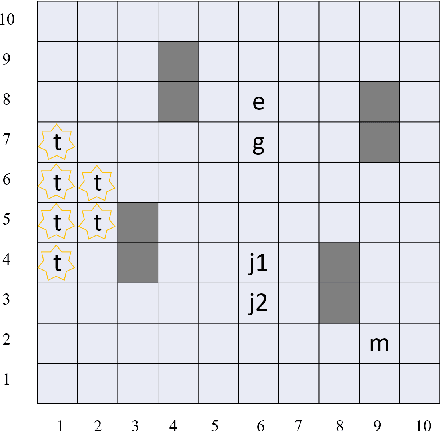
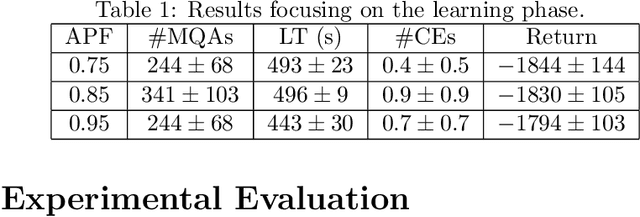
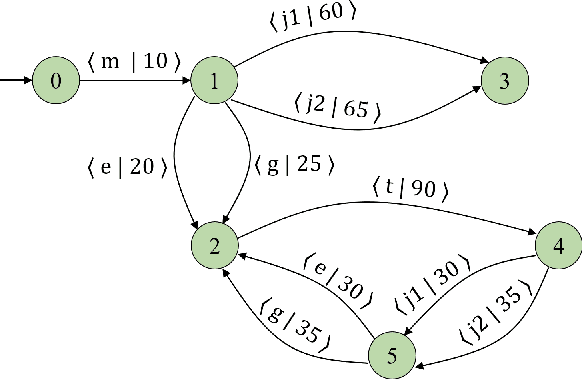
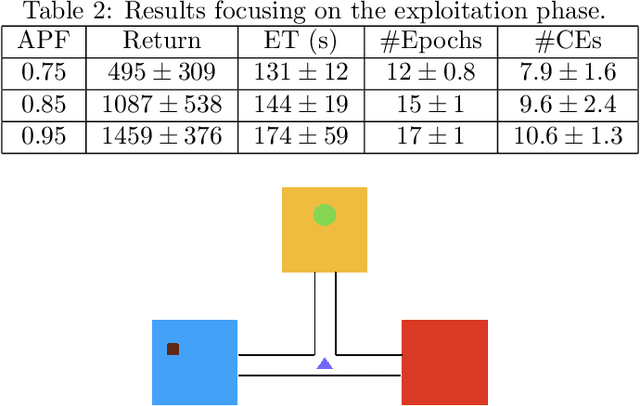
There are situations in which an agent should receive rewards only after having accomplished a series of previous tasks. In other words, the reward that the agent receives is non-Markovian. One natural and quite general way to represent history-dependent rewards is via a Mealy machine; a finite state automaton that produces output sequences (rewards in our case) from input sequences (state/action observations in our case). In our formal setting, we consider a Markov decision process (MDP) that models the dynamic of the environment in which the agent evolves and a Mealy machine synchronised with this MDP to formalise the non-Markovian reward function. While the MDP is known by the agent, the reward function is unknown from the agent and must be learnt. Learning non-Markov reward functions is a challenge. Our approach to overcome this challenging problem is a careful combination of the Angluin's L* active learning algorithm to learn finite automata, testing techniques for establishing conformance of finite model hypothesis and optimisation techniques for computing optimal strategies in Markovian (immediate) reward MDPs. We also show how our framework can be combined with classical heuristics such as Monte Carlo Tree Search. We illustrate our algorithms and a preliminary implementation on two typical examples for AI.

Learning-Based Mean-Payoff Optimization in an Unknown MDP under Omega-Regular Constraints

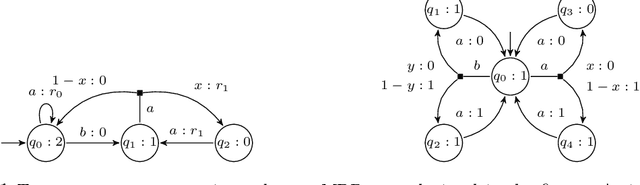
We formalize the problem of maximizing the mean-payoff value with high probability while satisfying a parity objective in a Markov decision process (MDP) with unknown probabilistic transition function and unknown reward function. Assuming the support of the unknown transition function and a lower bound on the minimal transition probability are known in advance, we show that in MDPs consisting of a single end component, two combinations of guarantees on the parity and mean-payoff objectives can be achieved depending on how much memory one is willing to use. (i) For all $\epsilon$ and $\gamma$ we can construct an online-learning finite-memory strategy that almost-surely satisfies the parity objective and which achieves an $\epsilon$-optimal mean payoff with probability at least $1 - \gamma$. (ii) Alternatively, for all $\epsilon$ and $\gamma$ there exists an online-learning infinite-memory strategy that satisfies the parity objective surely and which achieves an $\epsilon$-optimal mean payoff with probability at least $1 - \gamma$. We extend the above results to MDPs consisting of more than one end component in a natural way. Finally, we show that the aforementioned guarantees are tight, i.e. there are MDPs for which stronger combinations of the guarantees cannot be ensured.

Threshold Constraints with Guarantees for Parity Objectives in Markov Decision Processes

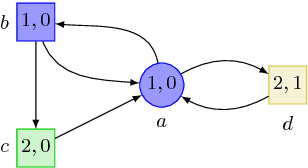
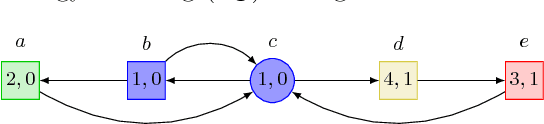
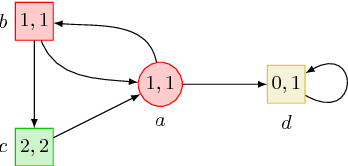
The beyond worst-case synthesis problem was introduced recently by Bruy\`ere et al. [BFRR14]: it aims at building system controllers that provide strict worst-case performance guarantees against an antagonistic environment while ensuring higher expected performance against a stochastic model of the environment. Our work extends the framework of [BFRR14] and follow-up papers, which focused on quantitative objectives, by addressing the case of $\omega$-regular conditions encoded as parity objectives, a natural way to represent functional requirements of systems. We build strategies that satisfy a main parity objective on all plays, while ensuring a secondary one with sufficient probability. This setting raises new challenges in comparison to quantitative objectives, as one cannot easily mix different strategies without endangering the functional properties of the system. We establish that, for all variants of this problem, deciding the existence of a strategy lies in ${\sf NP} \cap {\sf coNP}$, the same complexity class as classical parity games. Hence, our framework provides additional modeling power while staying in the same complexity class. [BFRR14] V\'eronique Bruy\`ere, Emmanuel Filiot, Mickael Randour, and Jean-Fran\c{c}ois Raskin. Meet your expectations with guarantees: Beyond worst-case synthesis in quantitative games. In Ernst W. Mayr and Natacha Portier, editors, 31st International Symposium on Theoretical Aspects of Computer Science, STACS 2014, March 5-8, 2014, Lyon, France, volume 25 of LIPIcs, pages 199-213. Schloss Dagstuhl - Leibniz - Zentrum fuer Informatik, 2014.