Complexity Controlled Generative Adversarial Networks

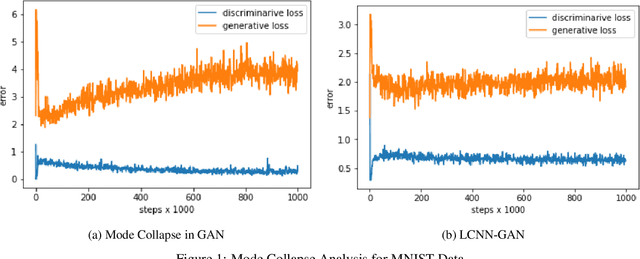
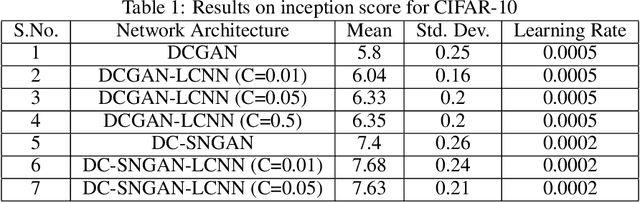
One of the issues faced in training Generative Adversarial Nets (GANs) and their variants is the problem of mode collapse, wherein the training stability in terms of the generative loss increases as more training data is used. In this paper, we propose an alternative architecture via the Low-Complexity Neural Network (LCNN), which attempts to learn models with low complexity. The motivation is that controlling model complexity leads to models that do not overfit the training data. We incorporate the LCNN loss function for GANs, Deep Convolutional GANs (DCGANs) and Spectral Normalized GANs (SNGANs), in order to develop hybrid architectures called the LCNN-GAN, LCNN-DCGAN and LCNN-SNGAN respectively. On various large benchmark image datasets, we show that the use of our proposed models results in stable training while avoiding the problem of mode collapse, resulting in better training stability. We also show how the learning behavior can be controlled by a hyperparameter in the LCNN functional, which also provides an improved inception score.

Enhash: A Fast Streaming Algorithm For Concept Drift Detection

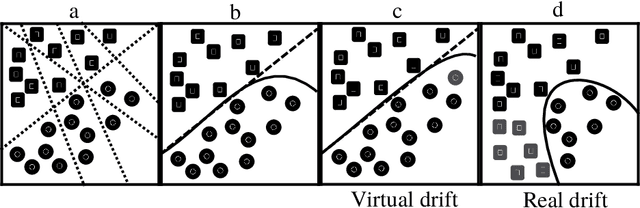
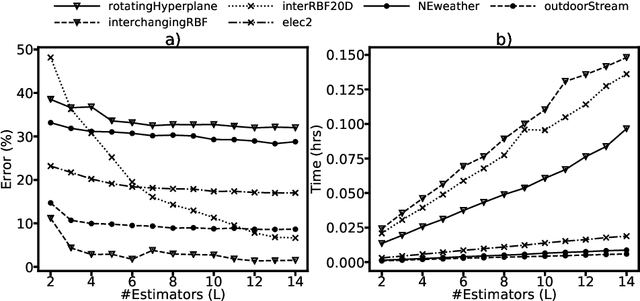
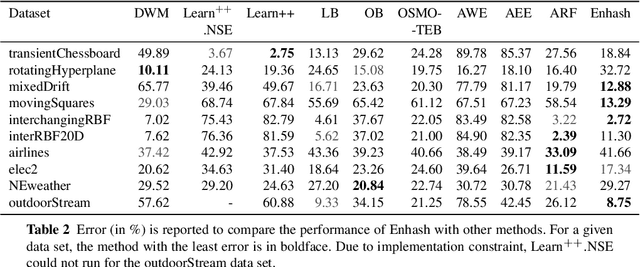
We propose Enhash, a fast ensemble learner that detects \textit{concept drift} in a data stream. A stream may consist of abrupt, gradual, virtual, or recurring events, or a mixture of various types of drift. Enhash employs projection hash to insert an incoming sample. We show empirically that the proposed method has competitive performance to existing ensemble learners in much lesser time. Also, Enhash has moderate resource requirements. Experiments relevant to performance comparison were performed on 6 artificial and 4 real data sets consisting of various types of drifts.

Guided Random Forest and its application to data approximation

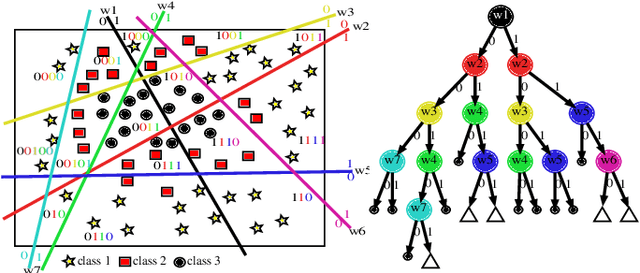
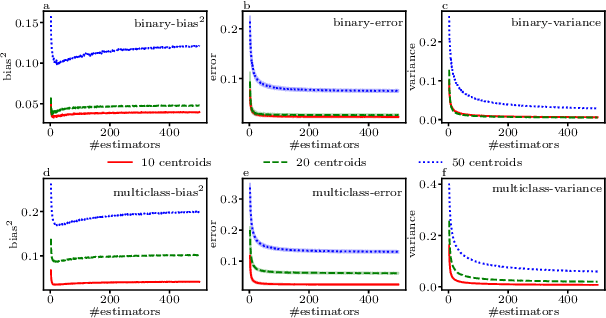
We present a new way of constructing an ensemble classifier, named the Guided Random Forest (GRAF) in the sequel. GRAF extends the idea of building oblique decision trees with localized partitioning to obtain a global partitioning. We show that global partitioning bridges the gap between decision trees and boosting algorithms. We empirically demonstrate that global partitioning reduces the generalization error bound. Results on 115 benchmark datasets show that GRAF yields comparable or better results on a majority of datasets. We also present a new way of approximating the datasets in the framework of random forests.

Smaller Models, Better Generalization

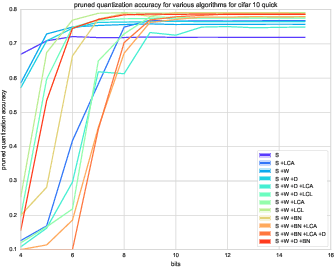
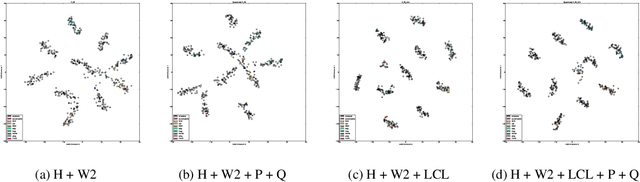
Reducing network complexity has been a major research focus in recent years with the advent of mobile technology. Convolutional Neural Networks that perform various vision tasks without memory overhaul is the need of the hour. This paper focuses on qualitative and quantitative analysis of reducing the network complexity using an upper bound on the Vapnik-Chervonenkis dimension, pruning, and quantization. We observe a general trend in improvement of accuracies as we quantize the models. We propose a novel loss function that helps in achieving considerable sparsity at comparable accuracies to that of dense models. We compare various regularizations prevalent in the literature and show the superiority of our method in achieving sparser models that generalize well.

Effect of Various Regularizers on Model Complexities of Neural Networks in Presence of Input Noise

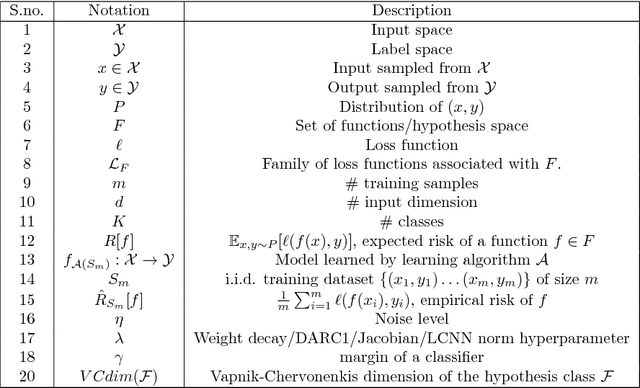
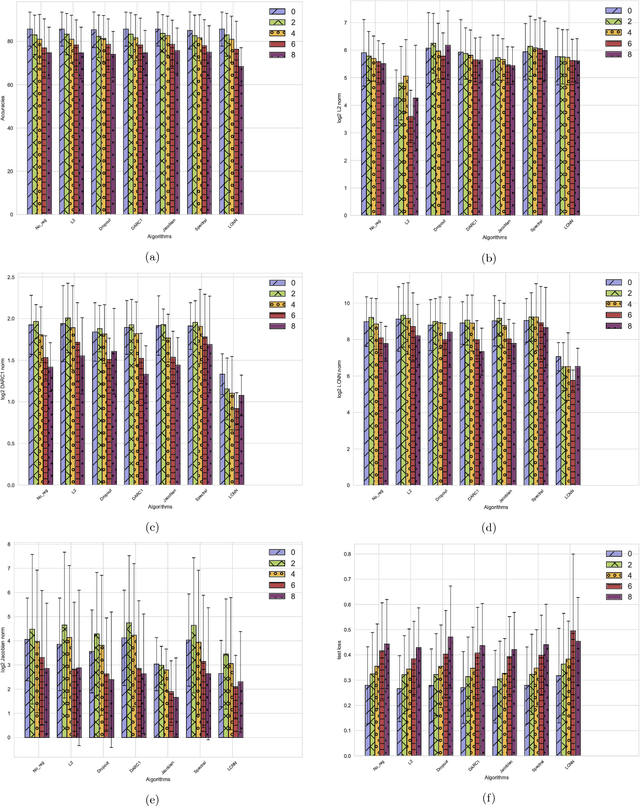
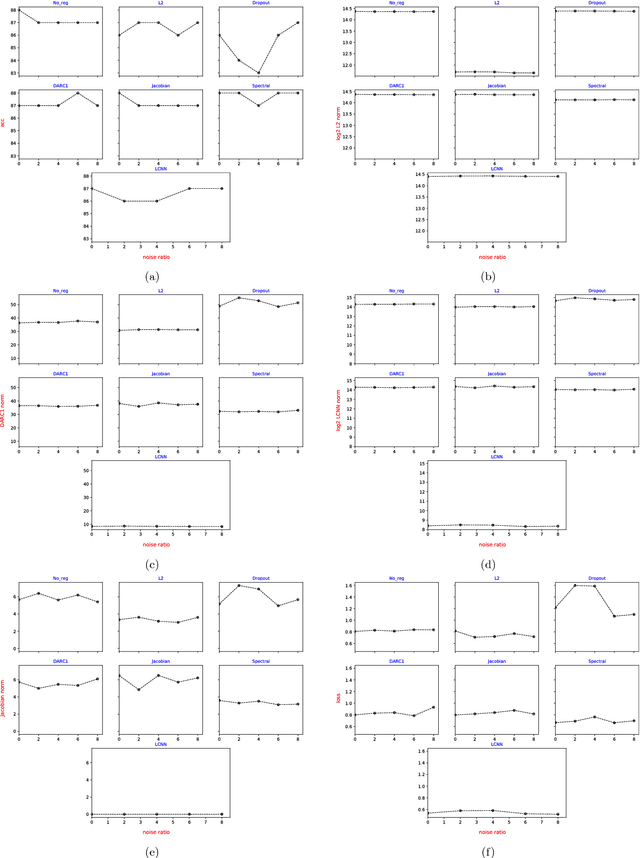
Deep neural networks are over-parameterized, which implies that the number of parameters are much larger than the number of samples used to train the network. Even in such a regime deep architectures do not overfit. This phenomenon is an active area of research and many theories have been proposed trying to understand this peculiar observation. These include the Vapnik Chervonenkis (VC) dimension bounds and Rademacher complexity bounds which show that the capacity of the network is characterized by the norm of weights rather than the number of parameters. However, the effect of input noise on these measures for shallow and deep architectures has not been studied. In this paper, we analyze the effects of various regularization schemes on the complexity of a neural network which we characterize with the loss, $L_2$ norm of the weights, Rademacher complexities (Directly Approximately Regularizing Complexity-DARC1), VC dimension based Low Complexity Neural Network (LCNN) when subject to varying degrees of Gaussian input noise. We show that $L_2$ regularization leads to a simpler hypothesis class and better generalization followed by DARC1 regularizer, both for shallow as well as deeper architectures. Jacobian regularizer works well for shallow architectures with high level of input noises. Spectral normalization attains highest test set accuracies both for shallow and deeper architectures. We also show that Dropout alone does not perform well in presence of input noise. Finally, we show that deeper architectures are robust to input noise as opposed to their shallow counterparts.

Radius-margin bounds for deep neural networks

Explaining the unreasonable effectiveness of deep learning has eluded researchers around the globe. Various authors have described multiple metrics to evaluate the capacity of deep architectures. In this paper, we allude to the radius margin bounds described for a support vector machine (SVM) with hinge loss, apply the same to the deep feed-forward architectures and derive the Vapnik-Chervonenkis (VC) bounds which are different from the earlier bounds proposed in terms of number of weights of the network. In doing so, we also relate the effectiveness of techniques like Dropout and Dropconnect in bringing down the capacity of the network. Finally, we describe the effect of maximizing the input as well as the output margin to achieve an input noise-robust deep architecture.

Scalable Twin Neural Networks for Classification of Unbalanced Data

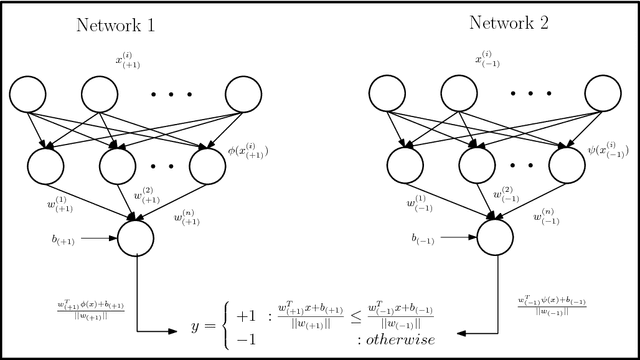
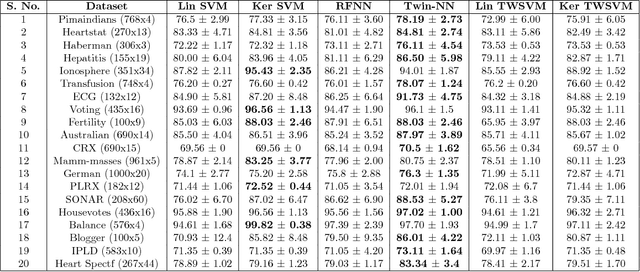
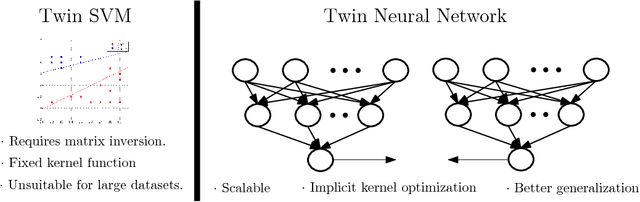
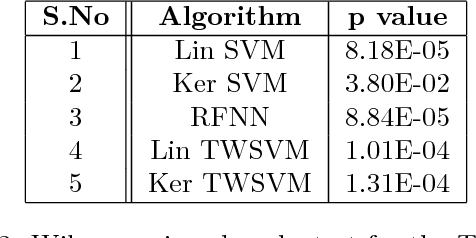
Twin Support Vector Machines (TWSVMs) have emerged an efficient alternative to Support Vector Machines (SVM) for learning from imbalanced datasets. The TWSVM learns two non-parallel classifying hyperplanes by solving a couple of smaller sized problems. However, it is unsuitable for large datasets, as it involves matrix operations. In this paper, we discuss a Twin Neural Network (Twin NN) architecture for learning from large unbalanced datasets. The Twin NN also learns an optimal feature map, allowing for better discrimination between classes. We also present an extension of this network architecture for multiclass datasets. Results presented in the paper demonstrate that the Twin NN generalizes well and scales well on large unbalanced datasets.

Learning Neural Network Classifiers with Low Model Complexity

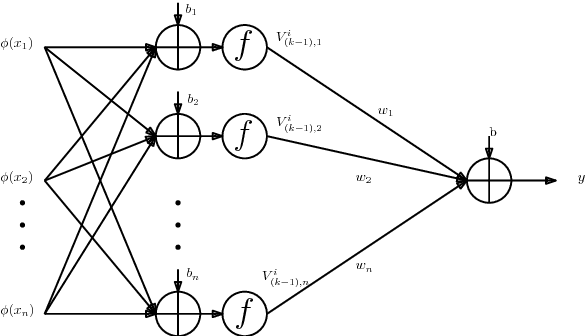
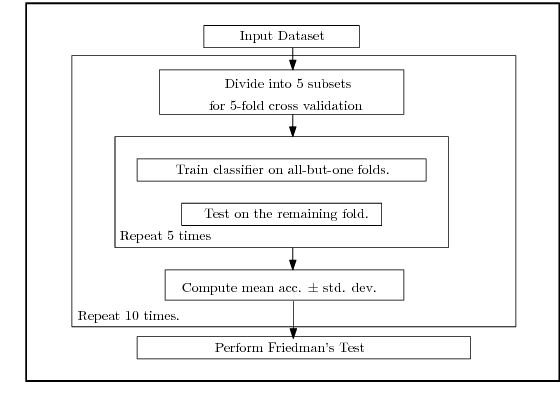
Modern neural network architectures for large-scale learning tasks have substantially higher model complexities, which makes understanding, visualizing and training these architectures difficult. Recent contributions to deep learning techniques have focused on architectural modifications to improve parameter efficiency and performance. In this paper, we derive a continuous and differentiable error functional for a neural network that minimizes its empirical error as well as a measure of the model complexity. The latter measure is obtained by deriving a differentiable upper bound on the Vapnik-Chervonenkis (VC) dimension of the classifier layer of a class of deep networks. Using standard backpropagation, we realize a training rule that tries to minimize the error on training samples, while improving generalization by keeping the model complexity low. We demonstrate the effectiveness of our formulation (the Low Complexity Neural Network - LCNN) across several deep learning algorithms, and a variety of large benchmark datasets. We show that hidden layer neurons in the resultant networks learn features that are crisp, and in the case of image datasets, quantitatively sharper. Our proposed approach yields benefits across a wide range of architectures, in comparison to and in conjunction with methods such as Dropout and Batch Normalization, and our results strongly suggest that deep learning techniques can benefit from model complexity control methods such as the LCNN learning rule.

Examining Representational Similarity in ConvNets and the Primate Visual Cortex

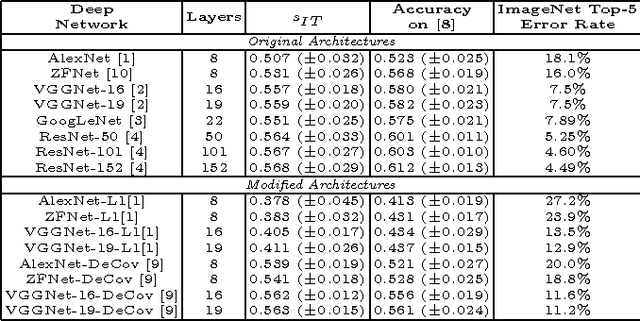
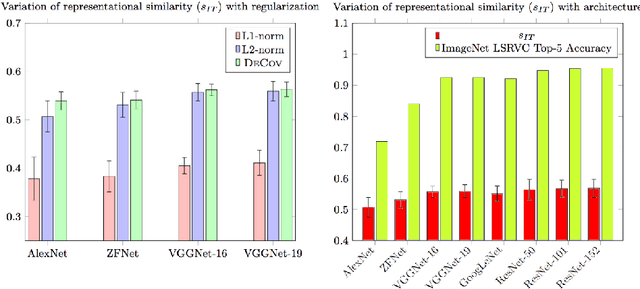
We compare several ConvNets with different depth and regularization techniques with multi-unit macaque IT cortex recordings and assess the impact of the same on representational similarity with the primate visual cortex. We find that with increasing depth and validation performance, ConvNet features are closer to cortical IT representations.

Feature Selection for classification of hyperspectral data by minimizing a tight bound on the VC dimension

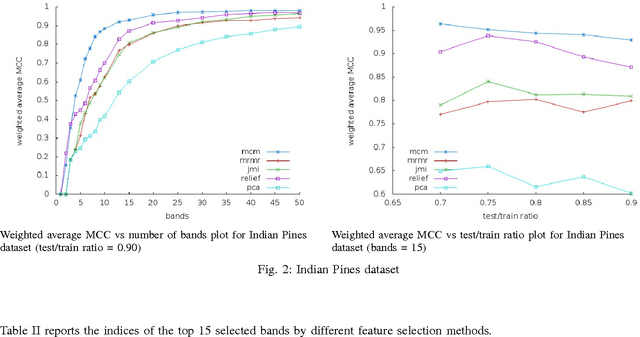
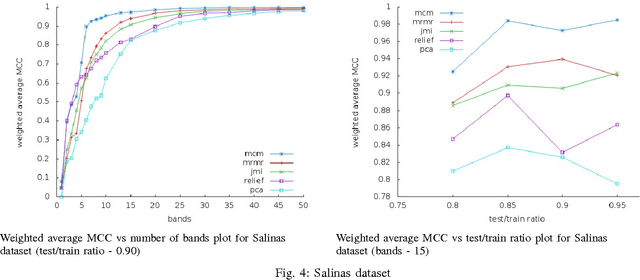
Hyperspectral data consists of large number of features which require sophisticated analysis to be extracted. A popular approach to reduce computational cost, facilitate information representation and accelerate knowledge discovery is to eliminate bands that do not improve the classification and analysis methods being applied. In particular, algorithms that perform band elimination should be designed to take advantage of the specifics of the classification method being used. This paper employs a recently proposed filter-feature-selection algorithm based on minimizing a tight bound on the VC dimension. We have successfully applied this algorithm to determine a reasonable subset of bands without any user-defined stopping criteria on widely used hyperspectral images and demonstrate that this method outperforms state-of-the-art methods in terms of both sparsity of feature set as well as accuracy of classification.\end{abstract}