EARL-BO: Reinforcement Learning for Multi-Step Lookahead, High-Dimensional Bayesian Optimization

Conventional methods for Bayesian optimization (BO) primarily involve one-step optimal decisions (e.g., maximizing expected improvement of the next step). To avoid myopic behavior, multi-step lookahead BO algorithms such as rollout strategies consider the sequential decision-making nature of BO, i.e., as a stochastic dynamic programming (SDP) problem, demonstrating promising results in recent years. However, owing to the curse of dimensionality, most of these methods make significant approximations or suffer scalability issues, e.g., being limited to two-step lookahead. This paper presents a novel reinforcement learning (RL)-based framework for multi-step lookahead BO in high-dimensional black-box optimization problems. The proposed method enhances the scalability and decision-making quality of multi-step lookahead BO by efficiently solving the SDP of the BO process in a near-optimal manner using RL. We first introduce an Attention-DeepSets encoder to represent the state of knowledge to the RL agent and employ off-policy learning to accelerate its initial training. We then propose a multi-task, fine-tuning procedure based on end-to-end (encoder-RL) on-policy learning. We evaluate the proposed method, EARL-BO (Encoder Augmented RL for Bayesian Optimization), on both synthetic benchmark functions and real-world hyperparameter optimization problems, demonstrating significantly improved performance compared to existing multi-step lookahead and high-dimensional BO methods.

Attention Mechanism for Lithium-Ion Battery Lifespan Prediction: Temporal and Cyclic Attention

Accurately predicting the lifespan of lithium-ion batteries (LIBs) is pivotal for optimizing usage and preventing accidents. Previous studies in constructing prediction models often relied on inputs challenging to measure in real-time operations and failed to capture intra-cycle and inter-cycle data patterns, essential features for accurate predictions, comprehensively. In this study, we employ attention mechanisms (AM) to develop data-driven models for predicting LIB lifespan using easily measurable inputs such as voltage, current, temperature, and capacity data. The developed model integrates recurrent neural network (RNN) and convolutional neural network (CNN) components, featuring two types of attention mechanisms: temporal attention (TA) and cyclic attention (CA). The inclusion of TA aims to identify important time steps within each cycle by scoring the hidden states of the RNN, whereas CA strives to capture key features of inter-cycle correlations through self-attention (SA). This enhances model accuracy and elucidates critical features in the input data. To validate our method, we apply it to publicly available cycling data consisting of three batches of cycling modes. The calculated TA scores highlight the rest phase as a key characteristic distinguishing LIB data among different batches. Additionally, CA scores reveal variations in the importance of cycles across batches. By leveraging CA scores, we explore the potential to reduce the number of cycles in the input data. The single-head and multi-head attentions enable us to decrease the input dimension from 100 to 50 and 30 cycles, respectively.

Dynamic penalty function approach for constraints handling in reinforcement learning

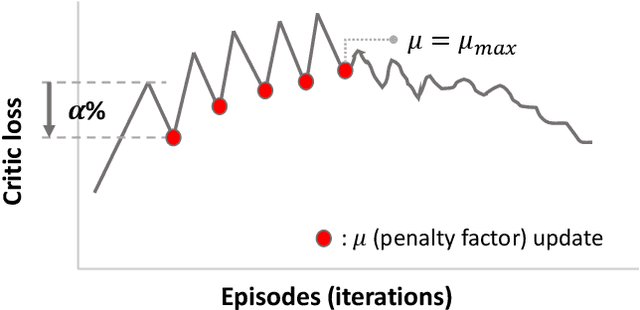
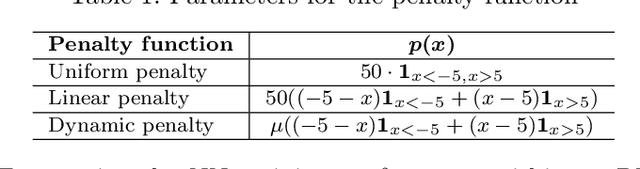
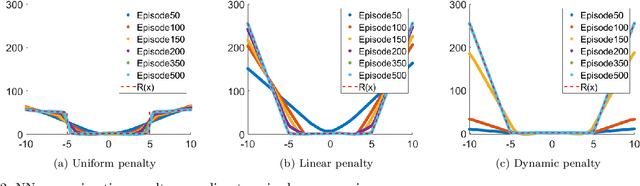
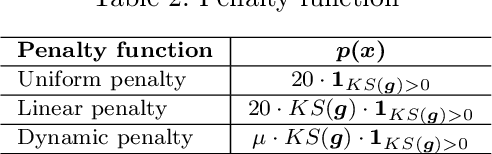
Reinforcement learning (RL) is attracting attentions as an effective way to solve sequential optimization problems involving high dimensional state/action space and stochastic uncertainties. Many of such problems involve constraints expressed by inequalities. This study focuses on using RL to solve such constrained optimal control problems. Most of RL application studies have considered inequality constraints as soft constraints by adding penalty terms for violating the constraints to the reward function. However, while training neural networks to represent the value (or Q) function, a key step in RL, one can run into computational issues caused by the sharp change in the function value at the constraint boundary due to the large penalty imposed. This difficulty during training can lead to convergence problems and ultimately poor closed-loop performance. To address this problem, this study suggests the use of a dynamic penalty function which gradually and systematically increases the penalty factor during training as the iteration episodes proceed. First, we examined the ability of a neural network to represent an artificial value function when uniform, linear, or dynamic penalty functions are added to prevent constraint violation. The agent trained by a Deep Q Network (DQN) algorithm with the dynamic penalty function approach was compared with agents with other constant penalty functions in a simple vehicle control problem. Results show that the dynamic penalty approach can improve the neural network's approximation accuracy and that brings faster convergence to a solution closer to the optimal solution.