FairML: A Julia Package for Fair Classification

In this paper, we propose FairML.jl, a Julia package providing a framework for fair classification in machine learning. In this framework, the fair learning process is divided into three stages. Each stage aims to reduce unfairness, such as disparate impact and disparate mistreatment, in the final prediction. For the preprocessing stage, we present a resampling method that addresses unfairness coming from data imbalances. The in-processing phase consist of a classification method. This can be either one coming from the MLJ.jl package, or a user defined one. For this phase, we incorporate fair ML methods that can handle unfairness to a certain degree through their optimization process. In the post-processing, we discuss the choice of the cut-off value for fair prediction. With simulations, we show the performance of the single phases and their combinations.

Fair Generalized Linear Mixed Models

When using machine learning for automated prediction, it is important to account for fairness in the prediction. Fairness in machine learning aims to ensure that biases in the data and model inaccuracies do not lead to discriminatory decisions. E.g., predictions from fair machine learning models should not discriminate against sensitive variables such as sexual orientation and ethnicity. The training data often in obtained from social surveys. In social surveys, oftentimes the data collection process is a strata sampling, e.g. due to cost restrictions. In strata samples, the assumption of independence between the observation is not fulfilled. Hence, if the machine learning models do not account for the strata correlations, the results may be biased. Especially high is the bias in cases where the strata assignment is correlated to the variable of interest. We present in this paper an algorithm that can handle both problems simultaneously, and we demonstrate the impact of stratified sampling on the quality of fair machine learning predictions in a reproducible simulation study.

Fair Mixed Effects Support Vector Machine

To ensure unbiased and ethical automated predictions, fairness must be a core principle in machine learning applications. Fairness in machine learning aims to mitigate biases present in the training data and model imperfections that could lead to discriminatory outcomes. This is achieved by preventing the model from making decisions based on sensitive characteristics like ethnicity or sexual orientation. A fundamental assumption in machine learning is the independence of observations. However, this assumption often does not hold true for data describing social phenomena, where data points are often clustered based. Hence, if the machine learning models do not account for the cluster correlations, the results may be biased. Especially high is the bias in cases where the cluster assignment is correlated to the variable of interest. We present a fair mixed effects support vector machine algorithm that can handle both problems simultaneously. With a reproducible simulation study we demonstrate the impact of clustered data on the quality of fair machine learning predictions.

Riemannian Optimization for Variance Estimation in Linear Mixed Models

Variance parameter estimation in linear mixed models is a challenge for many classical nonlinear optimization algorithms due to the positive-definiteness constraint of the random effects covariance matrix. We take a completely novel view on parameter estimation in linear mixed models by exploiting the intrinsic geometry of the parameter space. We formulate the problem of residual maximum likelihood estimation as an optimization problem on a Riemannian manifold. Based on the introduced formulation, we give geometric higher-order information on the problem via the Riemannian gradient and the Riemannian Hessian. Based on that, we test our approach with Riemannian optimization algorithms numerically. Our approach yields a higher quality of the variance parameter estimates compared to existing approaches.

A Riemannian Newton Trust-Region Method for Fitting Gaussian Mixture Models

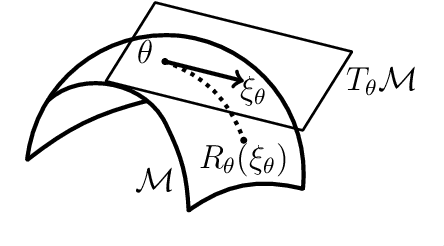
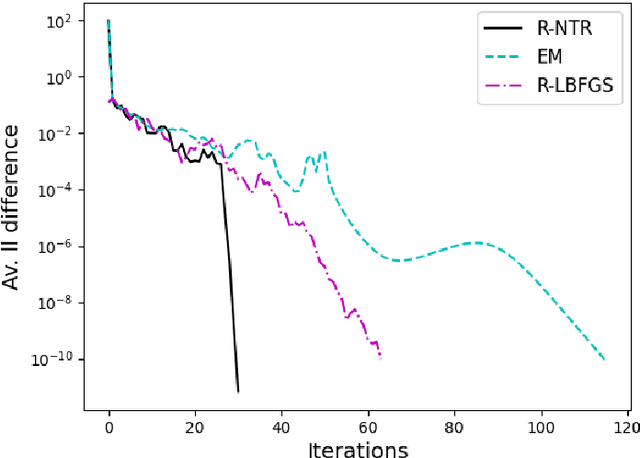
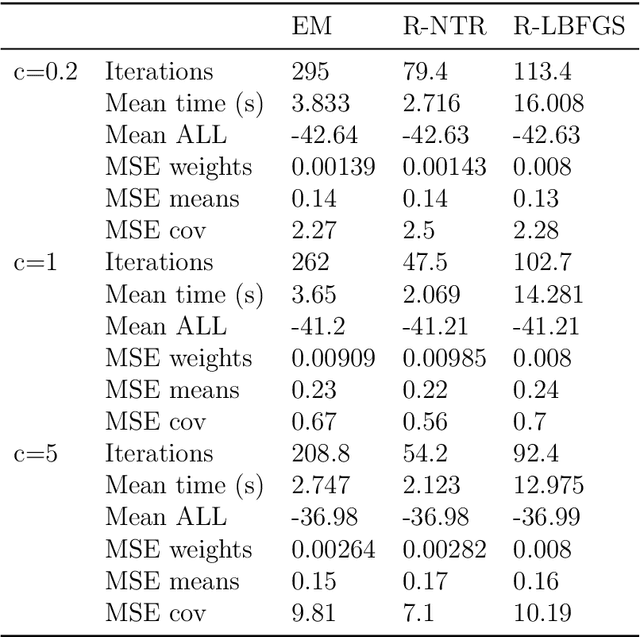
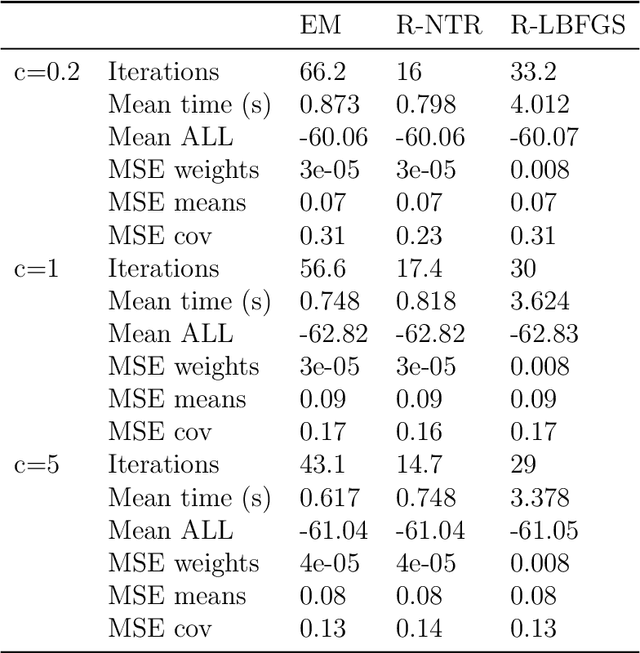
Gaussian Mixture Models are a powerful tool in Data Science and Statistics that are mainly used for clustering and density approximation. The task of estimating the model parameters is in practice often solved by the Expectation Maximization (EM) algorithm which has its benefits in its simplicity and low per-iteration costs. However, the EM converges slowly if there is a large share of hidden information or overlapping clusters. Recent advances in Manifold Optimization for Gaussian Mixture Models have gained increasing interest. We introduce a formula for the Riemannian Hessian for Gaussian Mixture Models. On top, we propose a new Riemannian Newton Trust-Region method which outperforms current approaches both in terms of runtime and number of iterations.