Generalized system identification with stable spline kernels

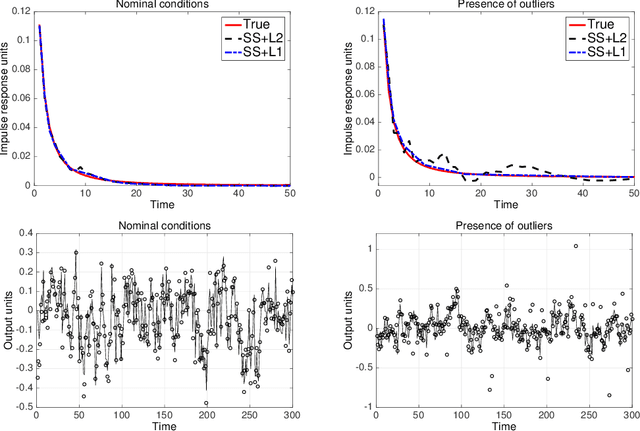
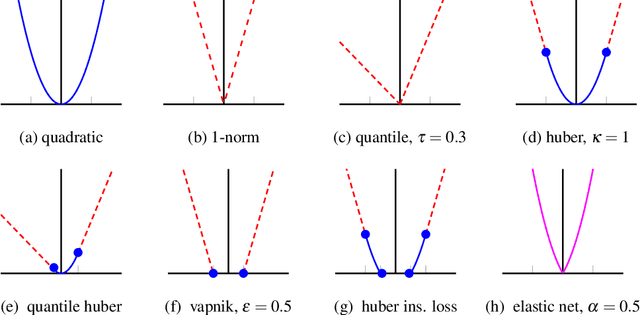
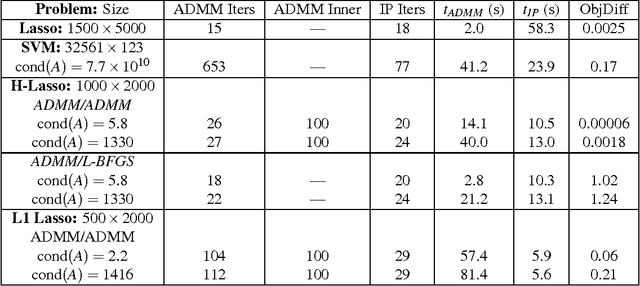
Regularized least-squares approaches have been successfully applied to linear system identification. Recent approaches use quadratic penalty terms on the unknown impulse response defined by stable spline kernels, which control model space complexity by leveraging regularity and bounded-input bounded-output stability. This paper extends linear system identification to a wide class of nonsmooth stable spline estimators, where regularization functionals and data misfits can be selected from a rich set of piecewise linear-quadratic (PLQ) penalties. This class includes the 1-norm, Huber, and Vapnik, in addition to the least-squares penalty. By representing penalties through their conjugates, the modeler can specify any piecewise linear-quadratic penalty for misfit and regularizer, as well as inequality constraints on the response. The interior-point solver we implement (IPsolve) is locally quadratically convergent, with $O(\min(m,n)^2(m+n))$ arithmetic operations per iteration, where $n$ the number of unknown impulse response coefficients and $m$ the number of observed output measurements. IPsolve is competitive with available alternatives for system identification. This is shown by a comparison with TFOCS, libSVM, and the FISTA algorithm. The code is open source (https://github.com/saravkin/IPsolve). The impact of the approach for system identification is illustrated with numerical experiments featuring robust formulations for contaminated data, relaxation systems, nonnegativity and unimodality constraints on the impulse response, and sparsity promoting regularization. Incorporating constraints yields particularly significant improvements.

Fast Robust Methods for Singular State-Space Models

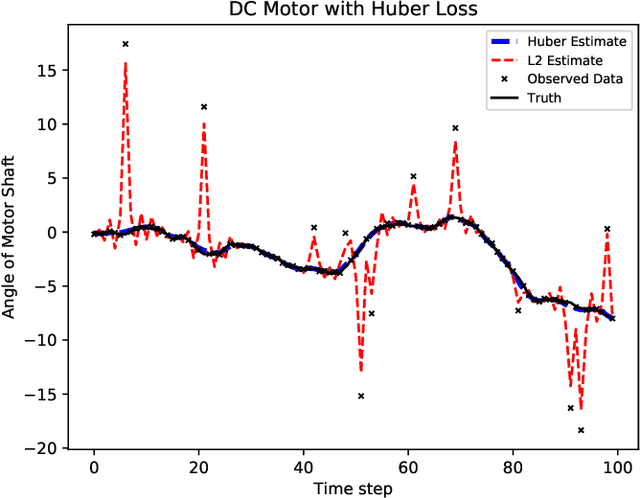
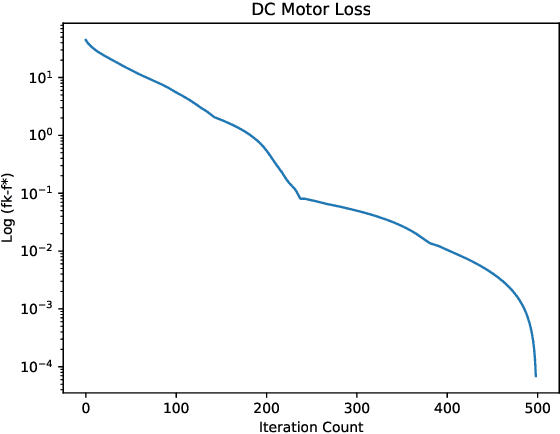
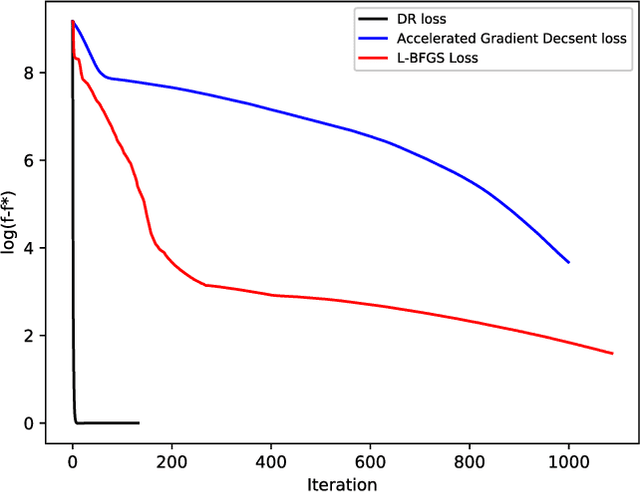
State-space models are used in a wide range of time series analysis formulations. Kalman filtering and smoothing are work-horse algorithms in these settings. While classic algorithms assume Gaussian errors to simplify estimation, recent advances use a broader range of optimization formulations to allow outlier-robust estimation, as well as constraints to capture prior information. Here we develop methods on state-space models where either innovations or error covariances may be singular. These models frequently arise in navigation (e.g. for `colored noise' models or deterministic integrals) and are ubiquitous in auto-correlated time series models such as ARMA. We reformulate all state-space models (singular as well as nonsinguar) as constrained convex optimization problems, and develop an efficient algorithm for this reformulation. The convergence rate is {\it locally linear}, with constants that do not depend on the conditioning of the problem. Numerical comparisons show that the new approach outperforms competing approaches for {\it nonsingular} models, including state of the art interior point (IP) methods. IP methods converge at superlinear rates; we expect them to dominate. However, the steep rate of the proposed approach (independent of problem conditioning) combined with cheap iterations wins against IP in a run-time comparison. We therefore suggest that the proposed approach be the {\it default choice} for estimating state space models outside of the Gaussian context, regardless of whether the error covariances are singular or not.

Convex Geometry of the Generalized Matrix-Fractional Function

Generalized matrix-fractional (GMF) functions are a class of matrix support functions introduced by Burke and Hoheisel as a tool for unifying a range of seemingly divergent matrix optimization problems associated with inverse problems, regularization and learning. In this paper we dramatically simplify the support function representation for GMF functions as well as the representation of their subdifferentials. These new representations allow the ready computation of a range of important related geometric objects whose formulations were previously unavailable.

Smoothing Dynamic Systems with State-Dependent Covariance Matrices

Kalman filtering and smoothing algorithms are used in many areas, including tracking and navigation, medical applications, and financial trend filtering. One of the basic assumptions required to apply the Kalman smoothing framework is that error covariance matrices are known and given. In this paper, we study a general class of inference problems where covariance matrices can depend functionally on unknown parameters. In the Kalman framework, this allows modeling situations where covariance matrices may depend functionally on the state sequence being estimated. We present an extended formulation and generalized Gauss-Newton (GGN) algorithm for inference in this context. When applied to dynamic systems inference, we show the algorithm can be implemented to preserve the computational efficiency of the classic Kalman smoother. The new approach is illustrated with a synthetic numerical example.

The connection between Bayesian estimation of a Gaussian random field and RKHS

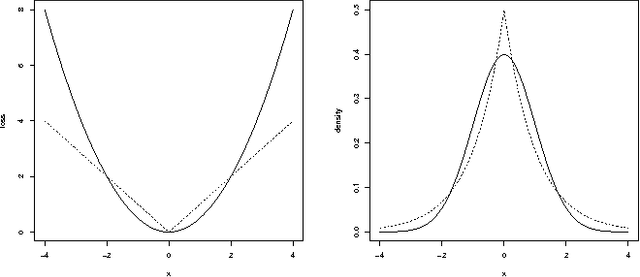
Reconstruction of a function from noisy data is often formulated as a regularized optimization problem over an infinite-dimensional reproducing kernel Hilbert space (RKHS). The solution describes the observed data and has a small RKHS norm. When the data fit is measured using a quadratic loss, this estimator has a known statistical interpretation. Given the noisy measurements, the RKHS estimate represents the posterior mean (minimum variance estimate) of a Gaussian random field with covariance proportional to the kernel associated with the RKHS. In this paper, we provide a statistical interpretation when more general losses are used, such as absolute value, Vapnik or Huber. Specifically, for any finite set of sampling locations (including where the data were collected), the MAP estimate for the signal samples is given by the RKHS estimate evaluated at these locations.

Sparse/Robust Estimation and Kalman Smoothing with Nonsmooth Log-Concave Densities: Modeling, Computation, and Theory

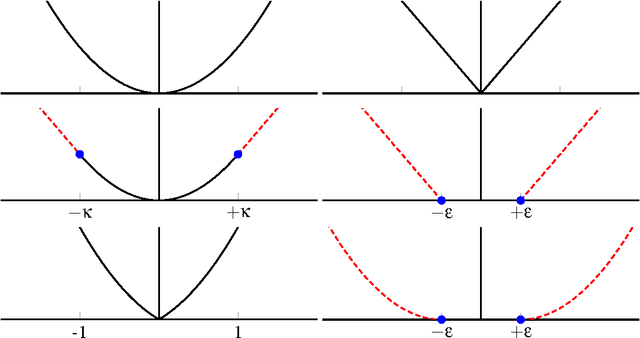
We introduce a class of quadratic support (QS) functions, many of which play a crucial role in a variety of applications, including machine learning, robust statistical inference, sparsity promotion, and Kalman smoothing. Well known examples include the l2, Huber, l1 and Vapnik losses. We build on a dual representation for QS functions using convex analysis, revealing the structure necessary for a QS function to be interpreted as the negative log of a probability density, and providing the foundation for statistical interpretation and analysis of QS loss functions. For a subclass of QS functions called piecewise linear quadratic (PLQ) penalties, we also develop efficient numerical estimation schemes. These components form a flexible statistical modeling framework for a variety of learning applications, together with a toolbox of efficient numerical methods for inference. In particular, for PLQ densities, interior point (IP) methods can be used. IP methods solve nonsmooth optimization problems by working directly with smooth systems of equations characterizing their optimality. The efficiency of the IP approach depends on the structure of particular applications. We consider the class of dynamic inverse problems using Kalman smoothing, where the aim is to reconstruct the state of a dynamical system with known process and measurement models starting from noisy output samples. In the classical case, Gaussian errors are assumed in the process and measurement models. The extended framework allows arbitrary PLQ densities to be used, and the proposed IP approach solves the generalized Kalman smoothing problem while maintaining the linear complexity in the size of the time series, just as in the Gaussian case. This extends the computational efficiency of classic algorithms to a much broader nonsmooth setting, and includes many recently proposed robust and sparse smoothers as special cases.

Robust and Trend Following Student's t Kalman Smoothers

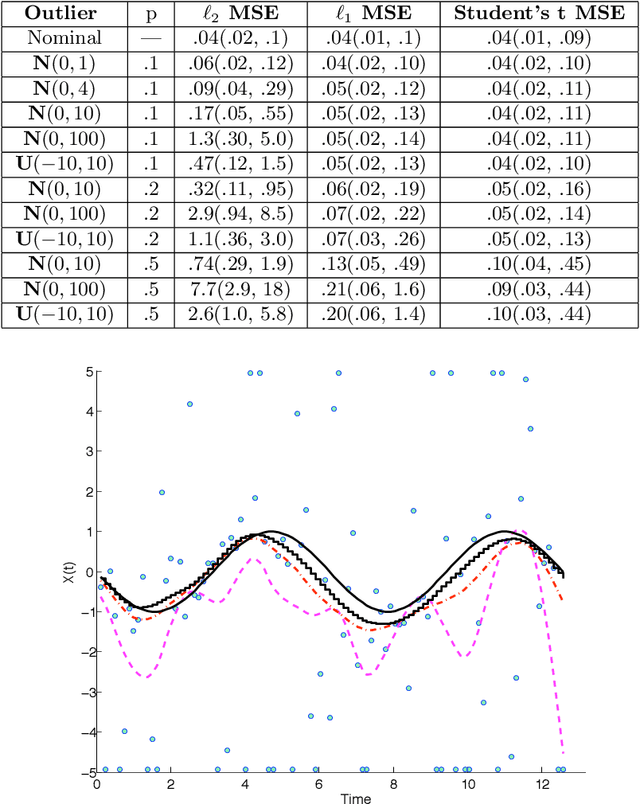
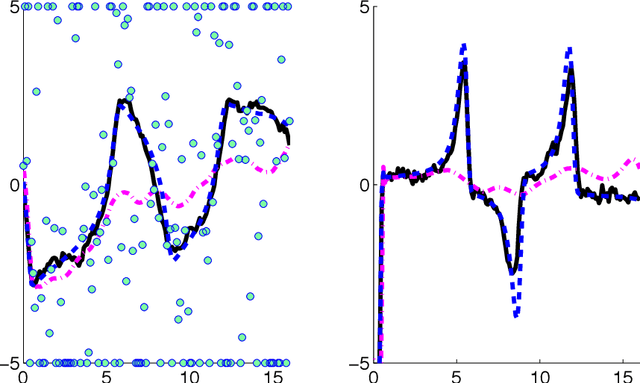
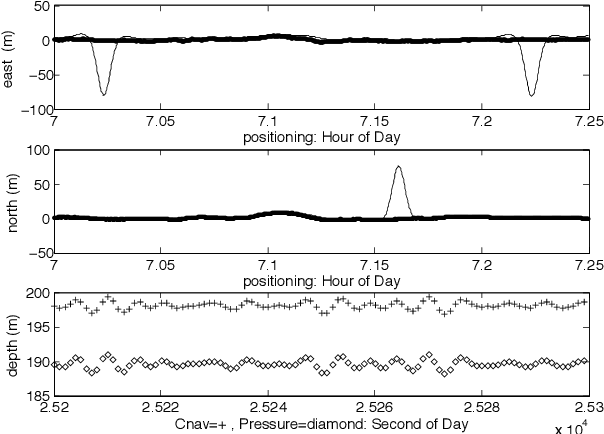
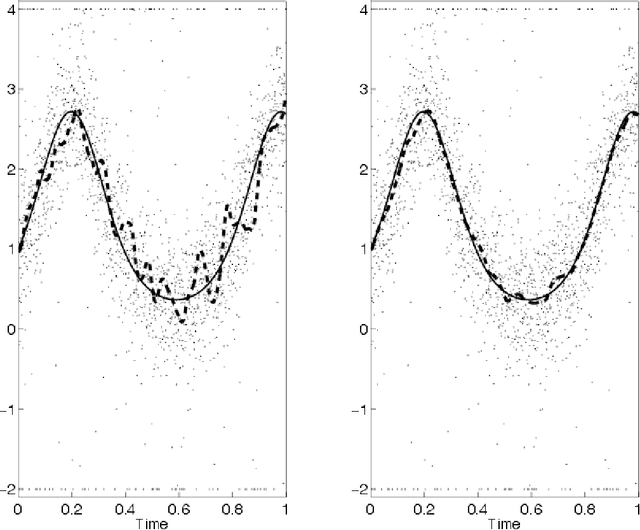
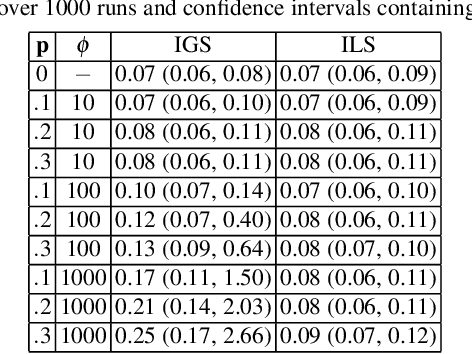
We present a Kalman smoothing framework based on modeling errors using the heavy tailed Student's t distribution, along with algorithms, convergence theory, open-source general implementation, and several important applications. The computational effort per iteration grows linearly with the length of the time series, and all smoothers allow nonlinear process and measurement models. Robust smoothers form an important subclass of smoothers within this framework. These smoothers work in situations where measurements are highly contaminated by noise or include data unexplained by the forward model. Highly robust smoothers are developed by modeling measurement errors using the Student's t distribution, and outperform the recently proposed L1-Laplace smoother in extreme situations with data containing 20% or more outliers. A second special application we consider in detail allows tracking sudden changes in the state. It is developed by modeling process noise using the Student's t distribution, and the resulting smoother can track sudden changes in the state. These features can be used separately or in tandem, and we present a general smoother algorithm and open source implementation, together with convergence analysis that covers a wide range of smoothers. A key ingredient of our approach is a technique to deal with the non-convexity of the Student's t loss function. Numerical results for linear and nonlinear models illustrate the performance of the new smoothers for robust and tracking applications, as well as for mixed problems that have both types of features.

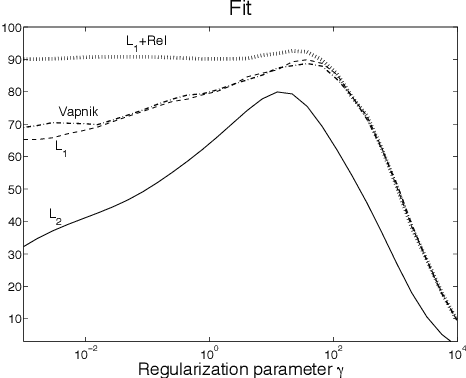
Linear system identification using stable spline kernels and PLQ penalties

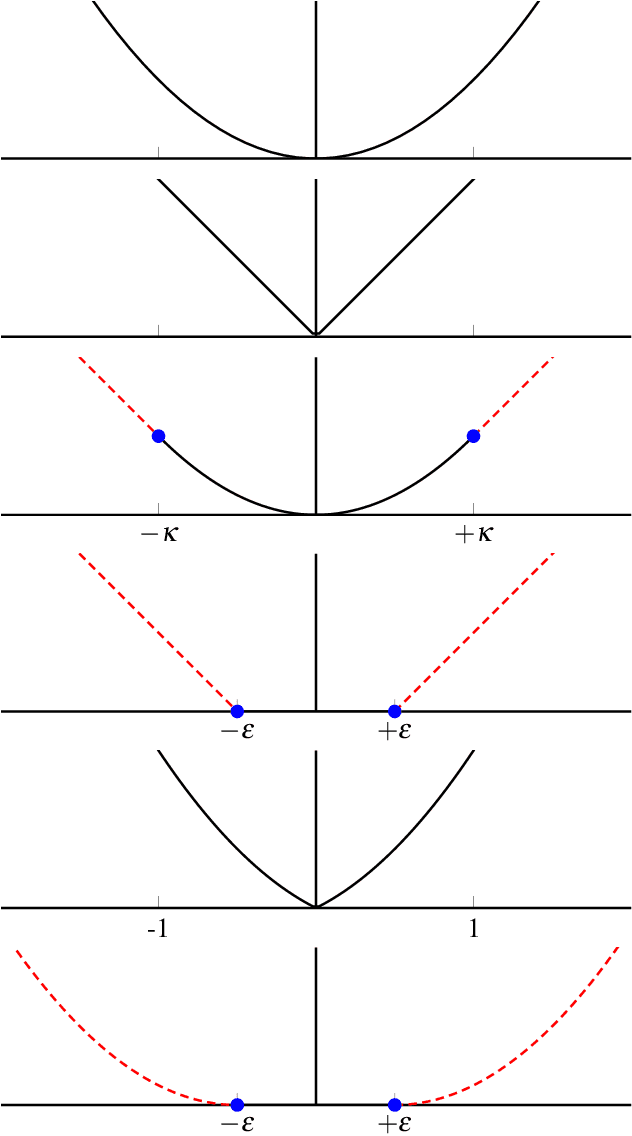
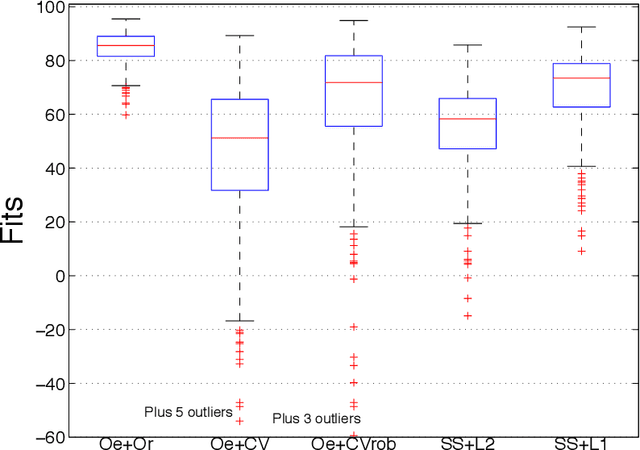
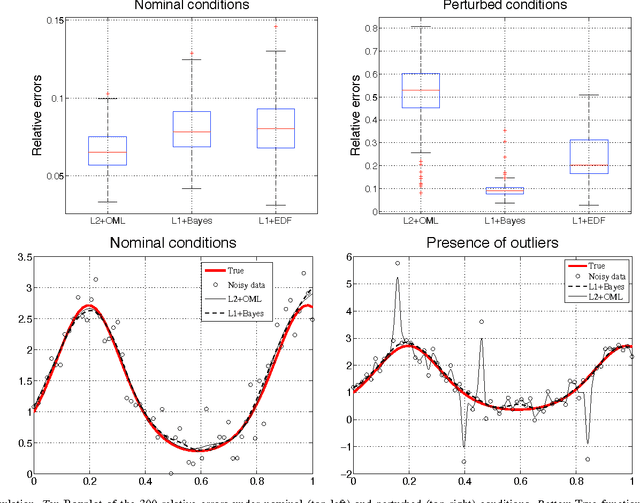
The classical approach to linear system identification is given by parametric Prediction Error Methods (PEM). In this context, model complexity is often unknown so that a model order selection step is needed to suitably trade-off bias and variance. Recently, a different approach to linear system identification has been introduced, where model order determination is avoided by using a regularized least squares framework. In particular, the penalty term on the impulse response is defined by so called stable spline kernels. They embed information on regularity and BIBO stability, and depend on a small number of parameters which can be estimated from data. In this paper, we provide new nonsmooth formulations of the stable spline estimator. In particular, we consider linear system identification problems in a very broad context, where regularization functionals and data misfits can come from a rich set of piecewise linear quadratic functions. Moreover, our anal- ysis includes polyhedral inequality constraints on the unknown impulse response. For any formulation in this class, we show that interior point methods can be used to solve the system identification problem, with complexity O(n3)+O(mn2) in each iteration, where n and m are the number of impulse response coefficients and measurements, respectively. The usefulness of the framework is illustrated via a numerical experiment where output measurements are contaminated by outliers.

Optimization viewpoint on Kalman smoothing, with applications to robust and sparse estimation

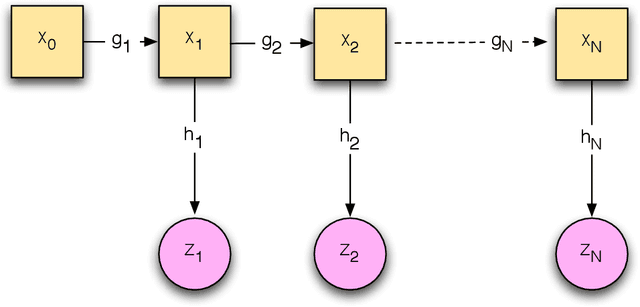
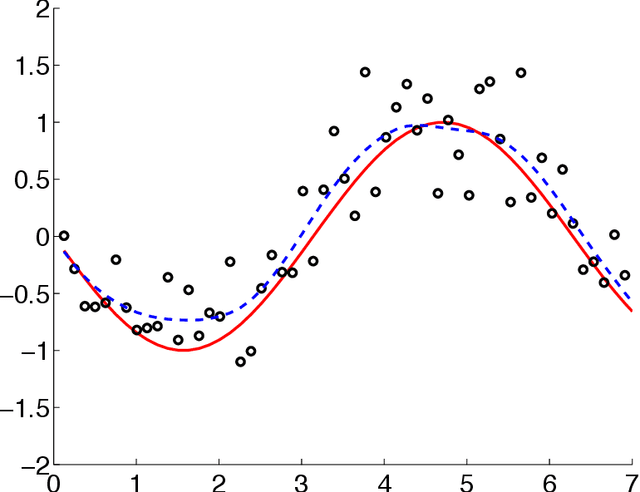
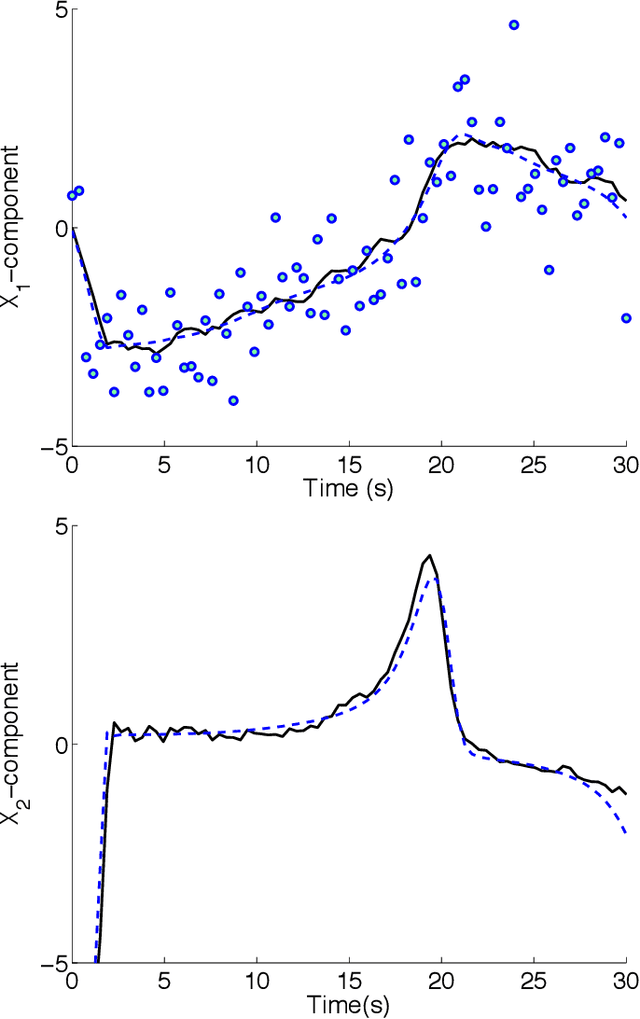
In this paper, we present the optimization formulation of the Kalman filtering and smoothing problems, and use this perspective to develop a variety of extensions and applications. We first formulate classic Kalman smoothing as a least squares problem, highlight special structure, and show that the classic filtering and smoothing algorithms are equivalent to a particular algorithm for solving this problem. Once this equivalence is established, we present extensions of Kalman smoothing to systems with nonlinear process and measurement models, systems with linear and nonlinear inequality constraints, systems with outliers in the measurements or sudden changes in the state, and systems where the sparsity of the state sequence must be accounted for. All extensions preserve the computational efficiency of the classic algorithms, and most of the extensions are illustrated with numerical examples, which are part of an open source Kalman smoothing Matlab/Octave package.

Convex vs nonconvex approaches for sparse estimation: GLasso, Multiple Kernel Learning and Hyperparameter GLasso

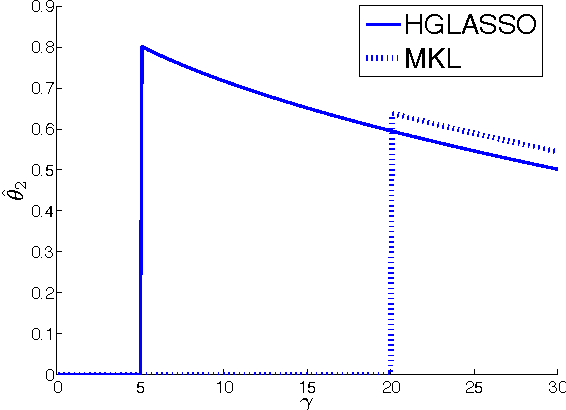
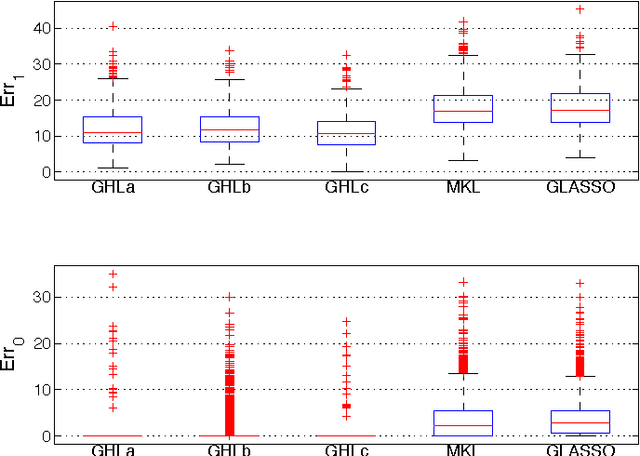
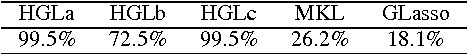
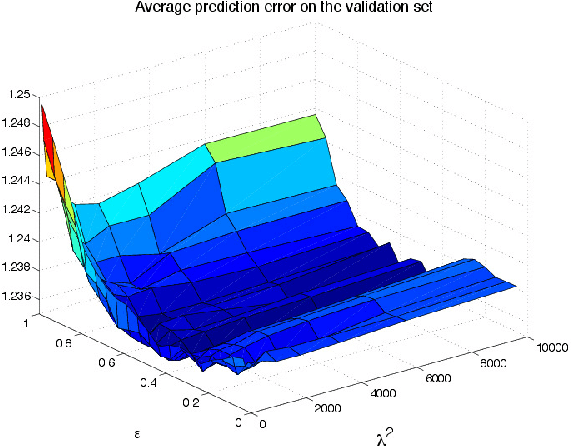
The popular Lasso approach for sparse estimation can be derived via marginalization of a joint density associated with a particular stochastic model. A different marginalization of the same probabilistic model leads to a different non-convex estimator where hyperparameters are optimized. Extending these arguments to problems where groups of variables have to be estimated, we study a computational scheme for sparse estimation that differs from the Group Lasso. Although the underlying optimization problem defining this estimator is non-convex, an initialization strategy based on a univariate Bayesian forward selection scheme is presented. This also allows us to define an effective non-convex estimator where only one scalar variable is involved in the optimization process. Theoretical arguments, independent of the correctness of the priors entering the sparse model, are included to clarify the advantages of this non-convex technique in comparison with other convex estimators. Numerical experiments are also used to compare the performance of these approaches.