KPFlow: An Operator Perspective on Dynamic Collapse Under Gradient Descent Training of Recurrent Networks

Gradient Descent (GD) and its variants are the primary tool for enabling efficient training of recurrent dynamical systems such as Recurrent Neural Networks (RNNs), Neural ODEs and Gated Recurrent units (GRUs). The dynamics that are formed in these models exhibit features such as neural collapse and emergence of latent representations that may support the remarkable generalization properties of networks. In neuroscience, qualitative features of these representations are used to compare learning in biological and artificial systems. Despite recent progress, there remains a need for theoretical tools to rigorously understand the mechanisms shaping learned representations, especially in finite, non-linear models. Here, we show that the gradient flow, which describes how the model's dynamics evolve over GD, can be decomposed into a product that involves two operators: a Parameter Operator, K, and a Linearized Flow Propagator, P. K mirrors the Neural Tangent Kernel in feed-forward neural networks, while P appears in Lyapunov stability and optimal control theory. We demonstrate two applications of our decomposition. First, we show how their interplay gives rise to low-dimensional latent dynamics under GD, and, specifically, how the collapse is a result of the network structure, over and above the nature of the underlying task. Second, for multi-task training, we show that the operators can be used to measure how objectives relevant to individual sub-tasks align. We experimentally and theoretically validate these findings, providing an efficient Pytorch package, \emph{KPFlow}, implementing robust analysis tools for general recurrent architectures. Taken together, our work moves towards building a next stage of understanding of GD learning in non-linear recurrent models.

Building Machine Learning Challenges for Anomaly Detection in Science

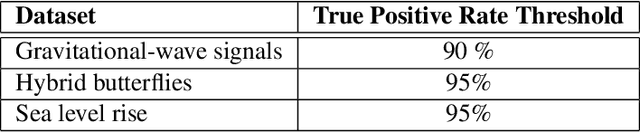
Scientific discoveries are often made by finding a pattern or object that was not predicted by the known rules of science. Oftentimes, these anomalous events or objects that do not conform to the norms are an indication that the rules of science governing the data are incomplete, and something new needs to be present to explain these unexpected outliers. The challenge of finding anomalies can be confounding since it requires codifying a complete knowledge of the known scientific behaviors and then projecting these known behaviors on the data to look for deviations. When utilizing machine learning, this presents a particular challenge since we require that the model not only understands scientific data perfectly but also recognizes when the data is inconsistent and out of the scope of its trained behavior. In this paper, we present three datasets aimed at developing machine learning-based anomaly detection for disparate scientific domains covering astrophysics, genomics, and polar science. We present the different datasets along with a scheme to make machine learning challenges around the three datasets findable, accessible, interoperable, and reusable (FAIR). Furthermore, we present an approach that generalizes to future machine learning challenges, enabling the possibility of large, more compute-intensive challenges that can ultimately lead to scientific discovery.

Evolutionary algorithms as an alternative to backpropagation for supervised training of Biophysical Neural Networks and Neural ODEs

Training networks consisting of biophysically accurate neuron models could allow for new insights into how brain circuits can organize and solve tasks. We begin by analyzing the extent to which the central algorithm for neural network learning -- stochastic gradient descent through backpropagation (BP) -- can be used to train such networks. We find that properties of biophysically based neural network models needed for accurate modelling such as stiffness, high nonlinearity and long evaluation timeframes relative to spike times makes BP unstable and divergent in a variety of cases. To address these instabilities and inspired by recent work, we investigate the use of "gradient-estimating" evolutionary algorithms (EAs) for training biophysically based neural networks. We find that EAs have several advantages making them desirable over direct BP, including being forward-pass only, robust to noisy and rigid losses, allowing for discrete loss formulations, and potentially facilitating a more global exploration of parameters. We apply our method to train a recurrent network of Morris-Lecar neuron models on a stimulus integration and working memory task, and show how it can succeed in cases where direct BP is inapplicable. To expand on the viability of EAs in general, we apply them to a general neural ODE problem and a stiff neural ODE benchmark and find again that EAs can out-perform direct BP here, especially for the over-parameterized regime. Our findings suggest that biophysical neurons could provide useful benchmarks for testing the limits of BP-adjacent methods, and demonstrate the viability of EAs for training networks with complex components.