Robust Trimmed k-means

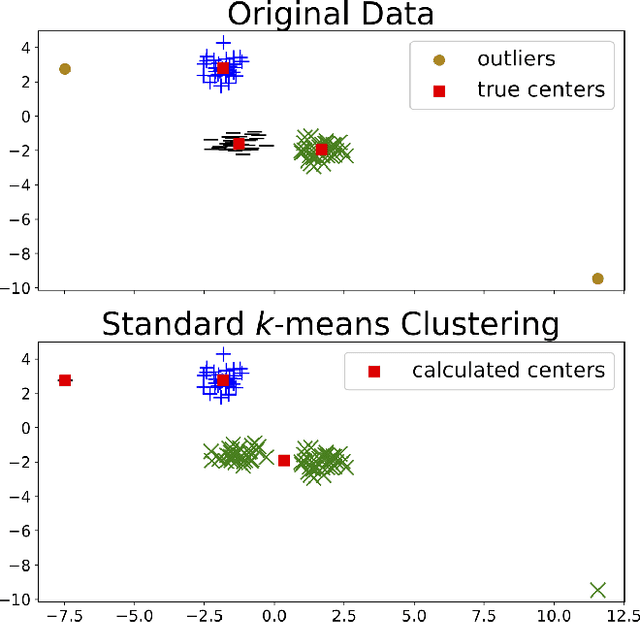
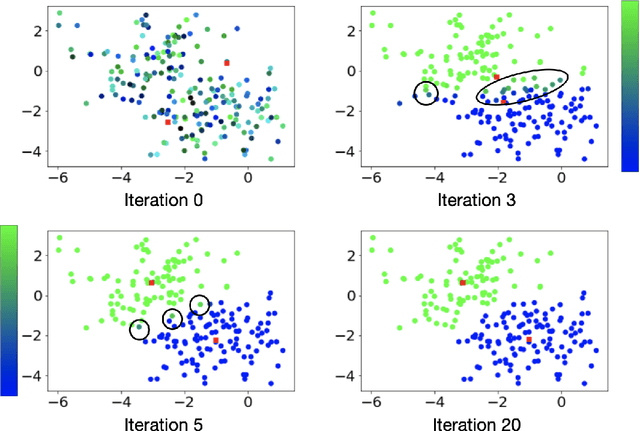
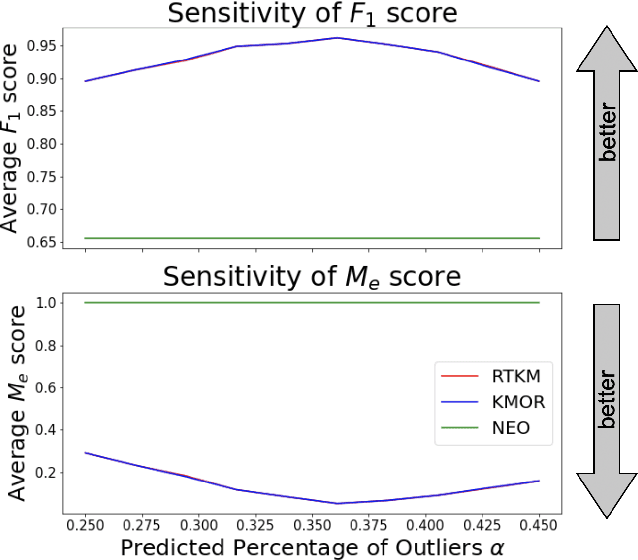
Clustering is a fundamental tool in unsupervised learning, used to group objects by distinguishing between similar and dissimilar features of a given data set. One of the most common clustering algorithms is k-means. Unfortunately, when dealing with real-world data many traditional clustering algorithms are compromised by lack of clear separation between groups, noisy observations, and/or outlying data points. Thus, robust statistical algorithms are required for successful data analytics. Current methods that robustify k-means clustering are specialized for either single or multi-membership data, but do not perform competitively in both cases. We propose an extension of the k-means algorithm, which we call Robust Trimmed k-means (RTKM) that simultaneously identifies outliers and clusters points and can be applied to either single- or multi-membership data. We test RTKM on various real-world datasets and show that RTKM performs competitively with other methods on single membership data with outliers and multi-membership data without outliers. We also show that RTKM leverages its relative advantages to outperform other methods on multi-membership data containing outliers.

Bagging, optimized dynamic mode decomposition (BOP-DMD) for robust, stable forecasting with spatial and temporal uncertainty-quantification

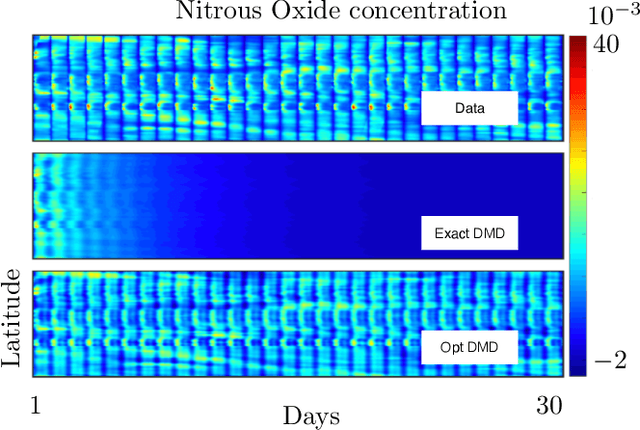
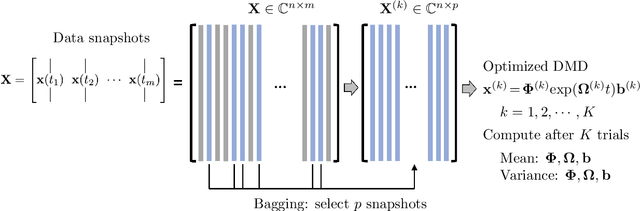
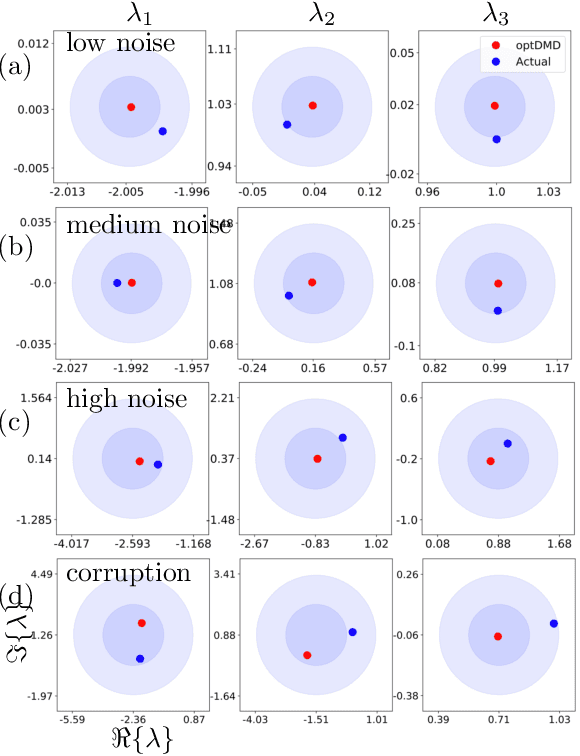
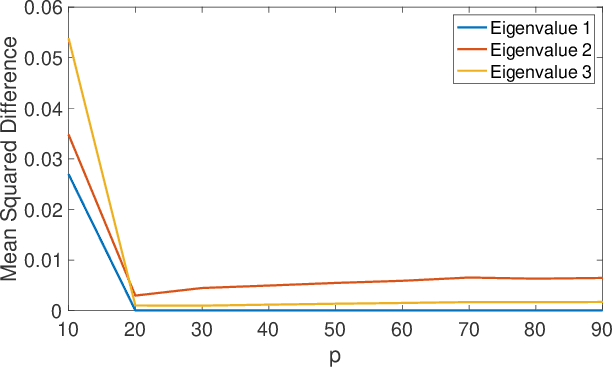
Dynamic mode decomposition (DMD) provides a regression framework for adaptively learning a best-fit linear dynamics model over snapshots of temporal, or spatio-temporal, data. A diversity of regression techniques have been developed for producing the linear model approximation whose solutions are exponentials in time. For spatio-temporal data, DMD provides low-rank and interpretable models in the form of dominant modal structures along with their exponential/oscillatory behavior in time. The majority of DMD algorithms, however, are prone to bias errors from noisy measurements of the dynamics, leading to poor model fits and unstable forecasting capabilities. The optimized DMD algorithm minimizes the model bias with a variable projection optimization, thus leading to stabilized forecasting capabilities. Here, the optimized DMD algorithm is improved by using statistical bagging methods whereby a single set of snapshots is used to produce an ensemble of optimized DMD models. The outputs of these models are averaged to produce a bagging, optimized dynamic mode decomposition (BOP-DMD). BOP-DMD not only improves performance, it also robustifies the model and provides both spatial and temporal uncertainty quantification (UQ). Thus unlike currently available DMD algorithms, BOP-DMD provides a stable and robust model for probabilistic, or Bayesian forecasting with comprehensive UQ metrics.

Deep Probabilistic Koopman: Long-term time-series forecasting under periodic uncertainties

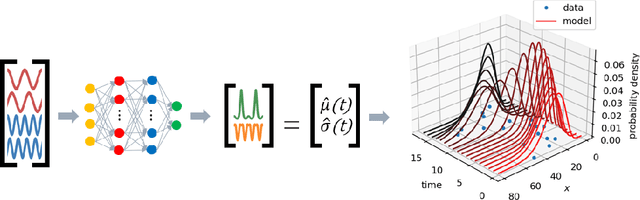
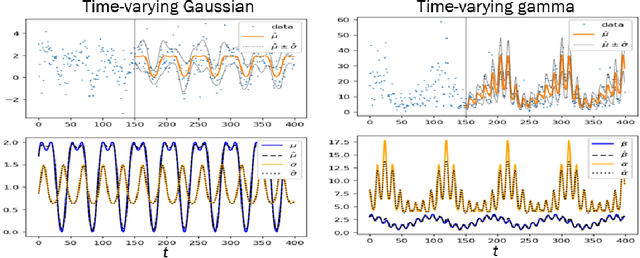
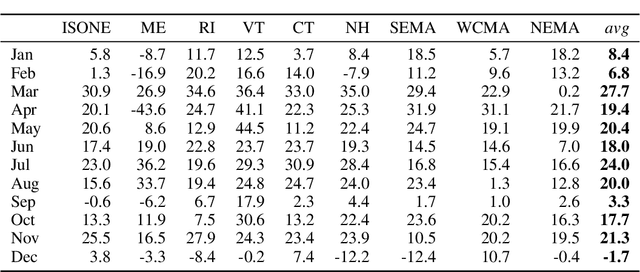
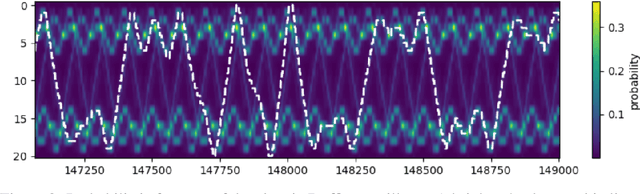
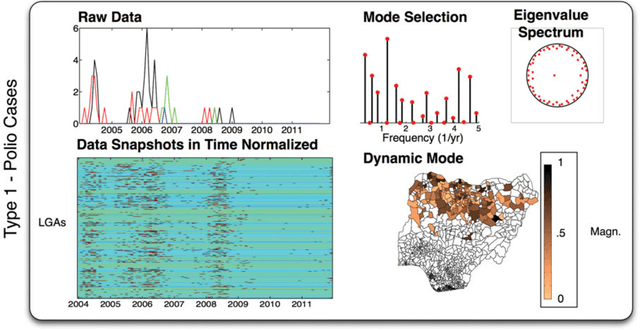
Probabilistic forecasting of complex phenomena is paramount to various scientific disciplines and applications. Despite the generality and importance of the problem, general mathematical techniques that allow for stable long-term forecasts with calibrated uncertainty measures are lacking. For most time series models, the difficulty of obtaining accurate probabilistic future time step predictions increases with the prediction horizon. In this paper, we introduce a surprisingly simple approach that characterizes time-varying distributions and enables reasonably accurate predictions thousands of timesteps into the future. This technique, which we call Deep Probabilistic Koopman (DPK), is based on recent advances in linear Koopman operator theory, and does not require time stepping for future time predictions. Koopman models also tend to have a small parameter footprint (often less than 10,000 parameters). We demonstrate the long-term forecasting performance of these models on a diversity of domains, including electricity demand forecasting, atmospheric chemistry, and neuroscience. For electricity demand modeling, our domain-agnostic technique outperforms all of 177 domain-specific competitors in the most recent Global Energy Forecasting Competition.

Learning normal form autoencoders for data-driven discovery of universal,parameter-dependent governing equations

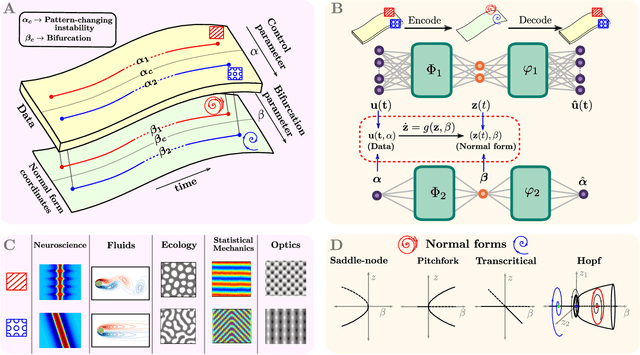
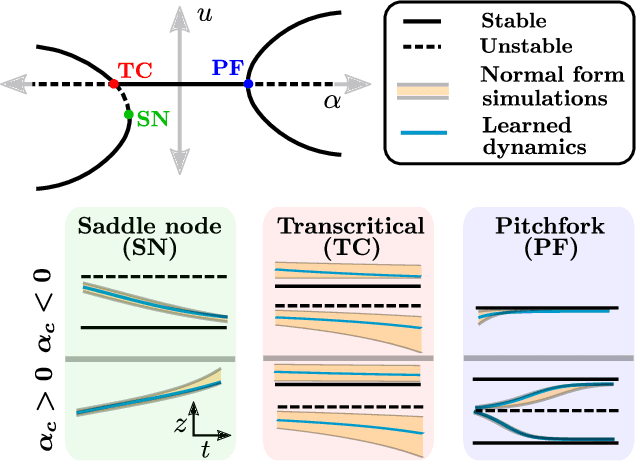
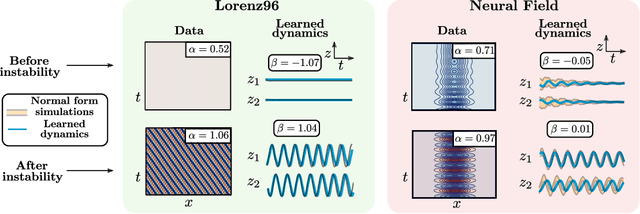
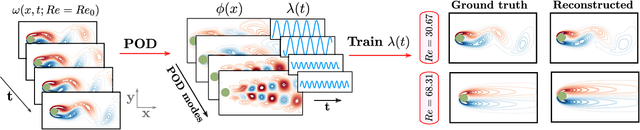
Complex systems manifest a small number of instabilities and bifurcations that are canonical in nature, resulting in universal pattern forming characteristics as a function of some parametric dependence. Such parametric instabilities are mathematically characterized by their universal un-foldings, or normal form dynamics, whereby a parsimonious model can be used to represent the dynamics. Although center manifold theory guarantees the existence of such low-dimensional normal forms, finding them has remained a long standing challenge. In this work, we introduce deep learning autoencoders to discover coordinate transformations that capture the underlying parametric dependence of a dynamical system in terms of its canonical normal form, allowing for a simple representation of the parametric dependence and bifurcation structure. The autoencoder constrains the latent variable to adhere to a given normal form, thus allowing it to learn the appropriate coordinate transformation. We demonstrate the method on a number of example problems, showing that it can capture a diverse set of normal forms associated with Hopf, pitchfork, transcritical and/or saddle node bifurcations. This method shows how normal forms can be leveraged as canonical and universal building blocks in deep learning approaches for model discovery and reduced-order modeling.

Extraction of instantaneous frequencies and amplitudes in nonstationary time-series data

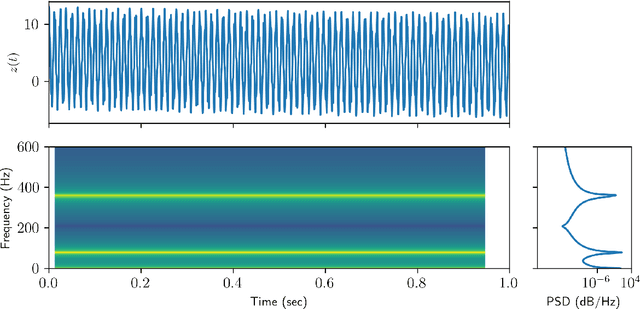
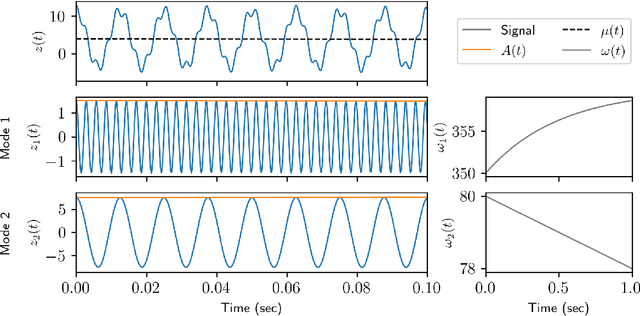
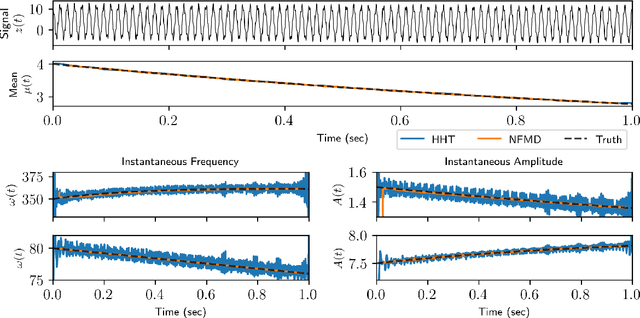
Time-series analysis is critical for a diversity of applications in science and engineering. By leveraging the strengths of modern gradient descent algorithms, the Fourier transform, multi-resolution analysis, and Bayesian spectral analysis, we propose a data-driven approach to time-frequency analysis that circumvents many of the shortcomings of classic approaches, including the extraction of nonstationary signals with discontinuities in their behavior. The method introduced is equivalent to a {\em nonstationary Fourier mode decomposition} (NFMD) for nonstationary and nonlinear temporal signals, allowing for the accurate identification of instantaneous frequencies and their amplitudes. The method is demonstrated on a diversity of time-series data, including on data from cantilever-based electrostatic force microscopy to quantify the time-dependent evolution of charging dynamics at the nanoscale.

Deep Learning of Conjugate Mappings

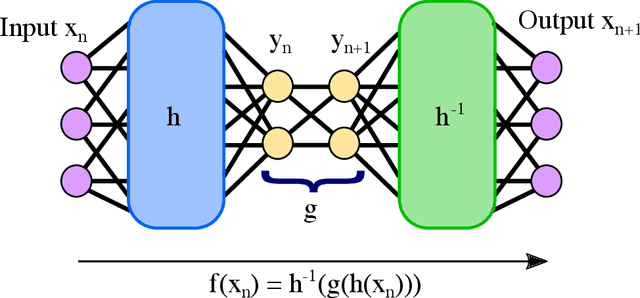
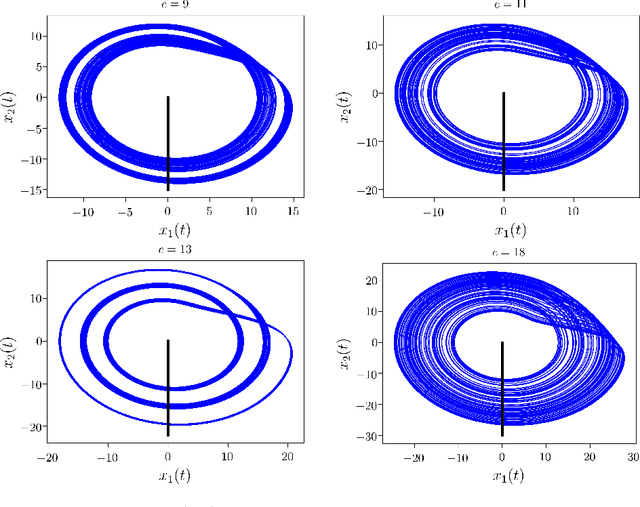
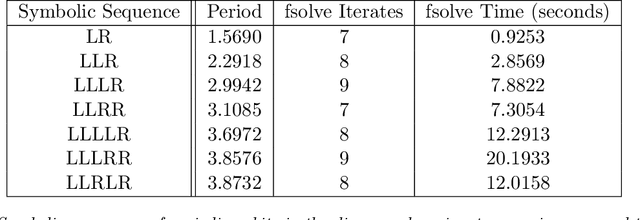
Despite many of the most common chaotic dynamical systems being continuous in time, it is through discrete time mappings that much of the understanding of chaos is formed. Henri Poincar\'e first made this connection by tracking consecutive iterations of the continuous flow with a lower-dimensional, transverse subspace. The mapping that iterates the dynamics through consecutive intersections of the flow with the subspace is now referred to as a Poincar\'e map, and it is the primary method available for interpreting and classifying chaotic dynamics. Unfortunately, in all but the simplest systems, an explicit form for such a mapping remains outstanding. This work proposes a method for obtaining explicit Poincar\'e mappings by using deep learning to construct an invertible coordinate transformation into a conjugate representation where the dynamics are governed by a relatively simple chaotic mapping. The invertible change of variable is based on an autoencoder, which allows for dimensionality reduction, and has the advantage of classifying chaotic systems using the equivalence relation of topological conjugacies. Indeed, the enforcement of topological conjugacies is the critical neural network regularization for learning the coordinate and dynamics pairing. We provide expository applications of the method to low-dimensional systems such as the R\"ossler and Lorenz systems, while also demonstrating the utility of the method on infinite-dimensional systems, such as the Kuramoto--Sivashinsky equation.

Modern Koopman Theory for Dynamical Systems

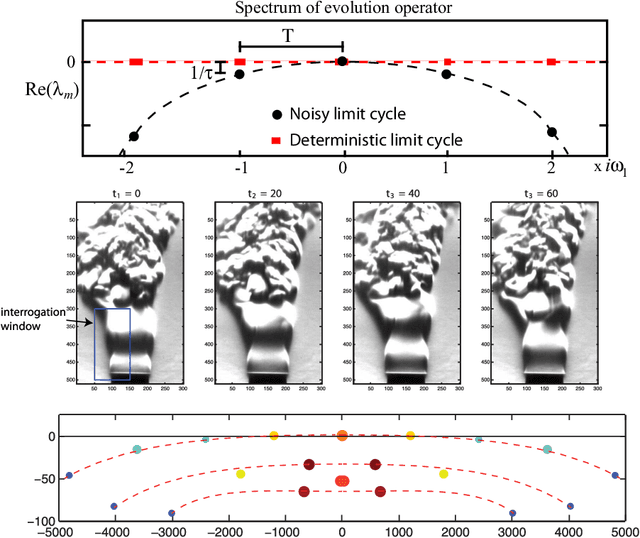
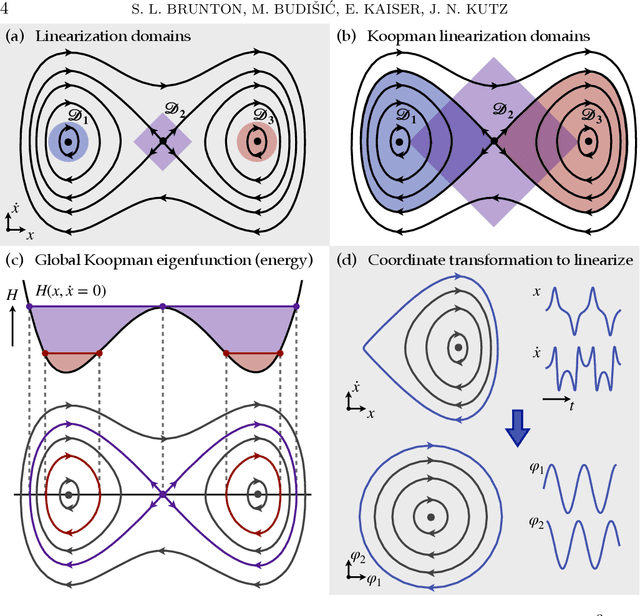
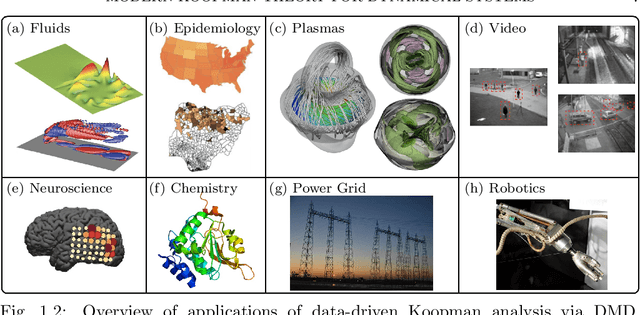
The field of dynamical systems is being transformed by the mathematical tools and algorithms emerging from modern computing and data science. First-principles derivations and asymptotic reductions are giving way to data-driven approaches that formulate models in operator theoretic or probabilistic frameworks. Koopman spectral theory has emerged as a dominant perspective over the past decade, in which nonlinear dynamics are represented in terms of an infinite-dimensional linear operator acting on the space of all possible measurement functions of the system. This linear representation of nonlinear dynamics has tremendous potential to enable the prediction, estimation, and control of nonlinear systems with standard textbook methods developed for linear systems. However, obtaining finite-dimensional coordinate systems and embeddings in which the dynamics appear approximately linear remains a central open challenge. The success of Koopman analysis is due primarily to three key factors: 1) there exists rigorous theory connecting it to classical geometric approaches for dynamical systems, 2) the approach is formulated in terms of measurements, making it ideal for leveraging big-data and machine learning techniques, and 3) simple, yet powerful numerical algorithms, such as the dynamic mode decomposition (DMD), have been developed and extended to reduce Koopman theory to practice in real-world applications. In this review, we provide an overview of modern Koopman operator theory, describing recent theoretical and algorithmic developments and highlighting these methods with a diverse range of applications. We also discuss key advances and challenges in the rapidly growing field of machine learning that are likely to drive future developments and significantly transform the theoretical landscape of dynamical systems.

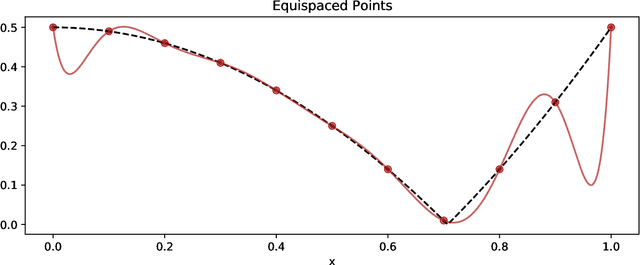
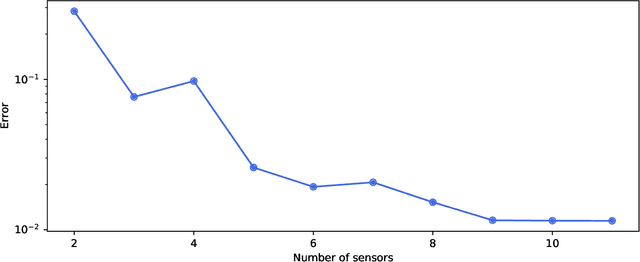
PySensors: A Python Package for Sparse Sensor Placement

PySensors is a Python package for selecting and placing a sparse set of sensors for classification and reconstruction tasks. Specifically, PySensors implements algorithms for data-driven sparse sensor placement optimization for reconstruction (SSPOR) and sparse sensor placement optimization for classification (SSPOC). In this work we provide a brief description of the mathematical algorithms and theory for sparse sensor optimization, along with an overview and demonstration of the features implemented in PySensors (with code examples). We also include practical advice for user and a list of potential extensions to PySensors. Software is available at https://github.com/dynamicslab/pysensors.

DeepGreen: Deep Learning of Green's Functions for Nonlinear Boundary Value Problems

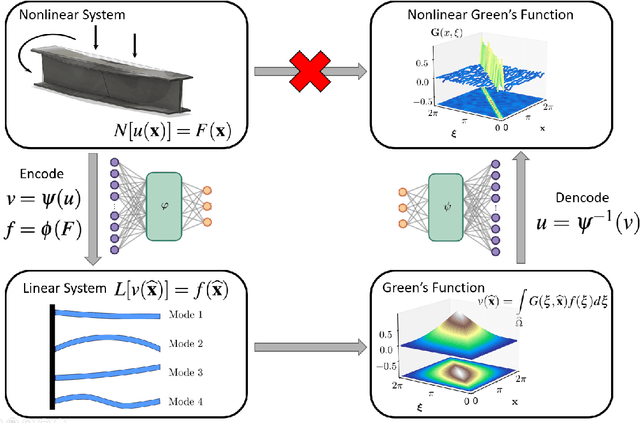
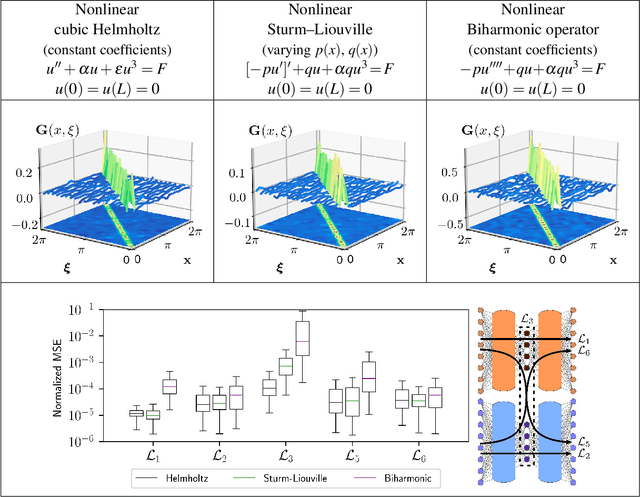
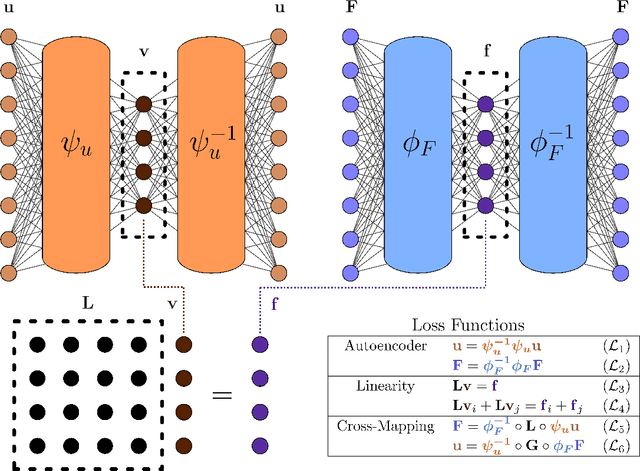
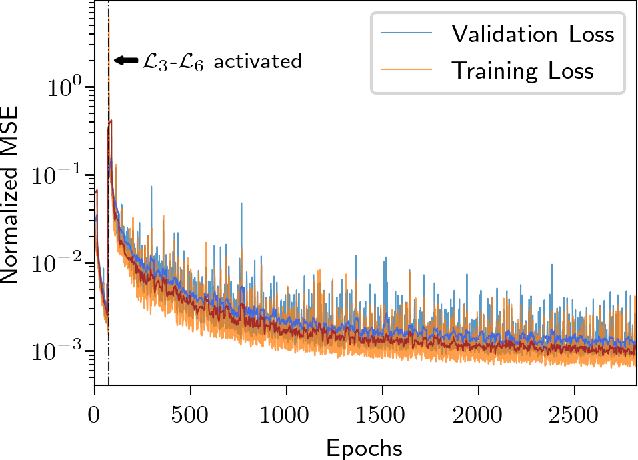
Boundary value problems (BVPs) play a central role in the mathematical analysis of constrained physical systems subjected to external forces. Consequently, BVPs frequently emerge in nearly every engineering discipline and span problem domains including fluid mechanics, electromagnetics, quantum mechanics, and elasticity. The fundamental solution, or Green's function, is a leading method for solving linear BVPs that enables facile computation of new solutions to systems under any external forcing. However, fundamental Green's function solutions for nonlinear BVPs are not feasible since linear superposition no longer holds. In this work, we propose a flexible deep learning approach to solve nonlinear BVPs using a dual-autoencoder architecture. The autoencoders discover an invertible coordinate transform that linearizes the nonlinear BVP and identifies both a linear operator $L$ and Green's function $G$ which can be used to solve new nonlinear BVPs. We find that the method succeeds on a variety of nonlinear systems including nonlinear Helmholtz and Sturm--Liouville problems, nonlinear elasticity, and a 2D nonlinear Poisson equation. The method merges the strengths of the universal approximation capabilities of deep learning with the physics knowledge of Green's functions to yield a flexible tool for identifying fundamental solutions to a variety of nonlinear systems.

Dynamic mode decomposition for forecasting and analysis of power grid load data

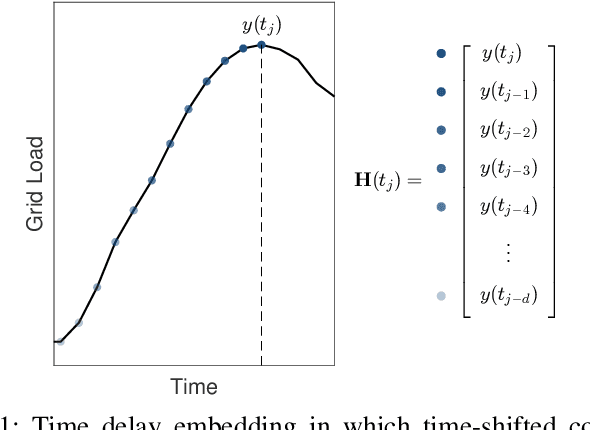
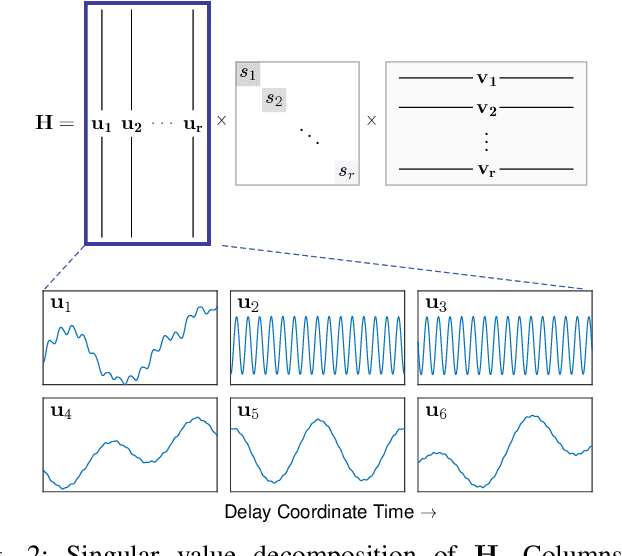
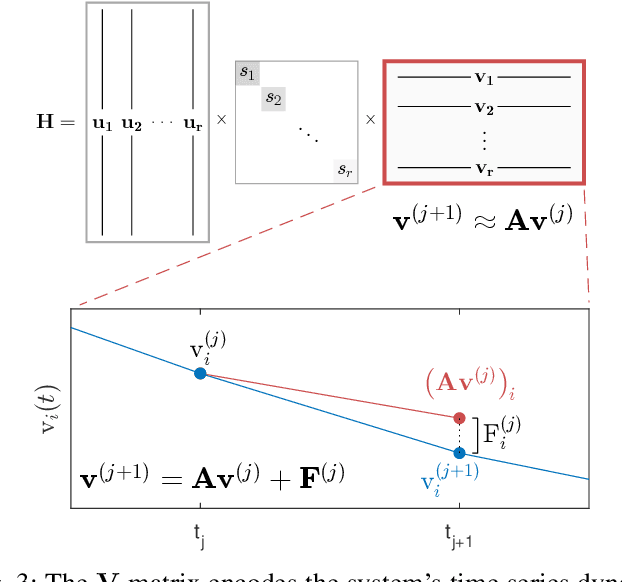
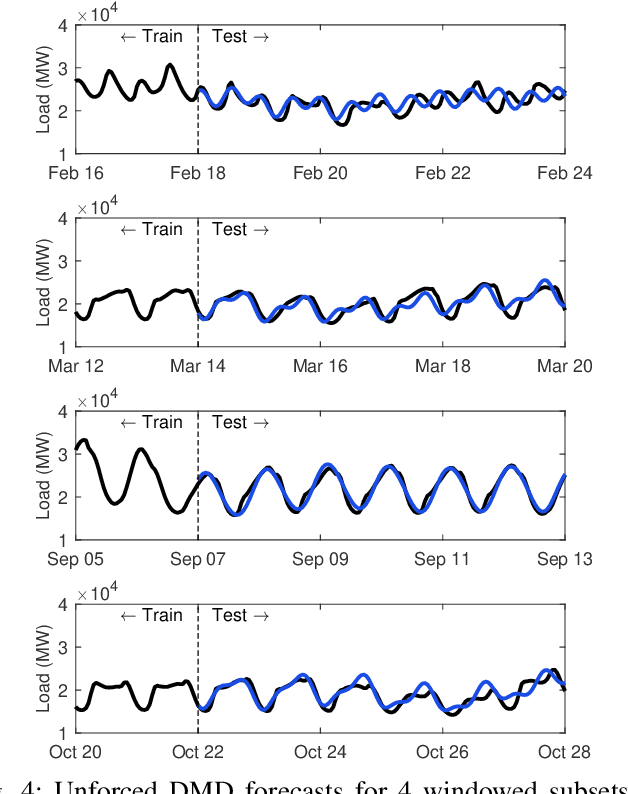
Time series forecasting remains a central challenge problem in almost all scientific disciplines, including load modeling in power systems engineering. The ability to produce accurate forecasts has major implications for real-time control, pricing, maintenance, and security decisions. We introduce a novel load forecasting method in which observed dynamics are modeled as a forced linear system using Dynamic Mode Decomposition (DMD) in time delay coordinates. Central to this approach is the insight that grid load, like many observables on complex real-world systems, has an "almost-periodic" character, i.e., a continuous Fourier spectrum punctuated by dominant peaks, which capture regular (e.g., daily or weekly) recurrences in the dynamics. The forecasting method presented takes advantage of this property by (i) regressing to a deterministic linear model whose eigenspectrum maps onto those peaks, and (ii) simultaneously learning a stochastic Gaussian process regression (GPR) process to actuate this system. Our forecasting algorithm is compared against state-of-the-art forecasting techniques not using additional explanatory variables and is shown to produce superior performance. Moreover, its use of linear intrinsic dynamics offers a number of desirable properties in terms of interpretability and parsimony.