Randomized Physics-Informed Neural Networks for Bayesian Data Assimilation

We propose a randomized physics-informed neural network (PINN) or rPINN method for uncertainty quantification in inverse partial differential equation (PDE) problems with noisy data. This method is used to quantify uncertainty in the inverse PDE PINN solutions. Recently, the Bayesian PINN (BPINN) method was proposed, where the posterior distribution of the PINN parameters was formulated using the Bayes' theorem and sampled using approximate inference methods such as the Hamiltonian Monte Carlo (HMC) and variational inference (VI) methods. In this work, we demonstrate that HMC fails to converge for non-linear inverse PDE problems. As an alternative to HMC, we sample the distribution by solving the stochastic optimization problem obtained by randomizing the PINN loss function. The effectiveness of the rPINN method is tested for linear and non-linear Poisson equations, and the diffusion equation with a high-dimensional space-dependent diffusion coefficient. The rPINN method provides informative distributions for all considered problems. For the linear Poisson equation, HMC and rPINN produce similar distributions, but rPINN is on average 27 times faster than HMC. For the non-linear Poison and diffusion equations, the HMC method fails to converge because a single HMC chain cannot sample multiple modes of the posterior distribution of the PINN parameters in a reasonable amount of time.

Randomized Physics-Informed Machine Learning for Uncertainty Quantification in High-Dimensional Inverse Problems

We propose a physics-informed machine learning method for uncertainty quantification in high-dimensional inverse problems. In this method, the states and parameters of partial differential equations (PDEs) are approximated with truncated conditional Karhunen-Lo\`eve expansions (CKLEs), which, by construction, match the measurements of the respective variables. The maximum a posteriori (MAP) solution of the inverse problem is formulated as a minimization problem over CKLE coefficients where the loss function is the sum of the norm of PDE residuals and the $\ell_2$ regularization term. This MAP formulation is known as the physics-informed CKLE (PICKLE) method. Uncertainty in the inverse solution is quantified in terms of the posterior distribution of CKLE coefficients, and we sample the posterior by solving a randomized PICKLE minimization problem, formulated by adding zero-mean Gaussian perturbations in the PICKLE loss function. We call the proposed approach the randomized PICKLE (rPICKLE) method. For linear and low-dimensional nonlinear problems (15 CKLE parameters), we show analytically and through comparison with Hamiltonian Monte Carlo (HMC) that the rPICKLE posterior converges to the true posterior given by the Bayes rule. For high-dimensional non-linear problems with 2000 CKLE parameters, we numerically demonstrate that rPICKLE posteriors are highly informative--they provide mean estimates with an accuracy comparable to the estimates given by the MAP solution and the confidence interval that mostly covers the reference solution. We are not able to obtain the HMC posterior to validate rPICKLE's convergence to the true posterior due to the HMC's prohibitive computational cost for the considered high-dimensional problems. Our results demonstrate the advantages of rPICKLE over HMC for approximately sampling high-dimensional posterior distributions subject to physics constraints.

Online Real-time Learning of Dynamical Systems from Noisy Streaming Data

Recent advancements in sensing and communication facilitate obtaining high-frequency real-time data from various physical systems like power networks, climate systems, biological networks, etc. However, since the data are recorded by physical sensors, it is natural that the obtained data is corrupted by measurement noise. In this paper, we present a novel algorithm for online real-time learning of dynamical systems from noisy time-series data, which employs the Robust Koopman operator framework to mitigate the effect of measurement noise. The proposed algorithm has three main advantages: a) it allows for online real-time monitoring of a dynamical system; b) it obtains a linear representation of the underlying dynamical system, thus enabling the user to use linear systems theory for analysis and control of the system; c) it is computationally fast and less intensive than the popular Extended Dynamic Mode Decomposition (EDMD) algorithm. We illustrate the efficiency of the proposed algorithm by applying it to identify the Van der Pol oscillator, the IEEE 68 bus system, and a ring network of Van der Pol oscillators.

Dynamic mode decomposition for forecasting and analysis of power grid load data

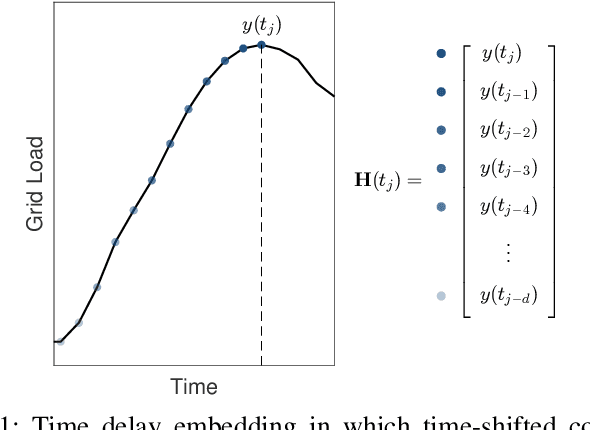
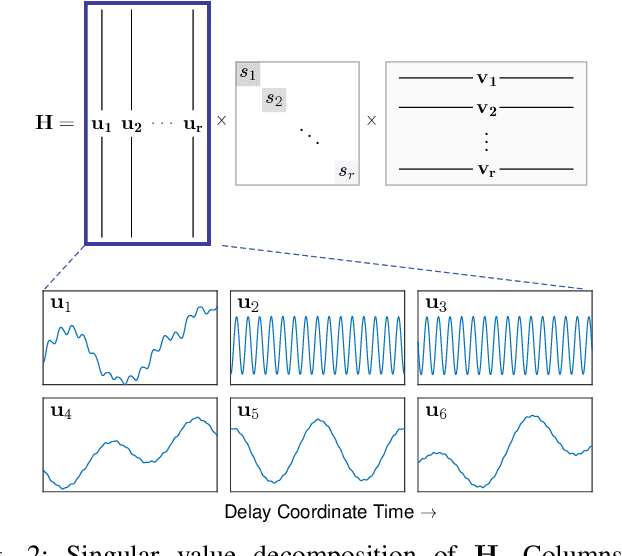
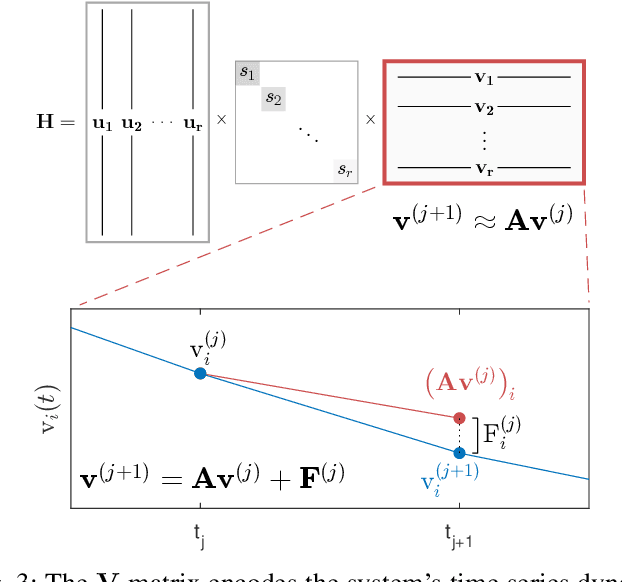
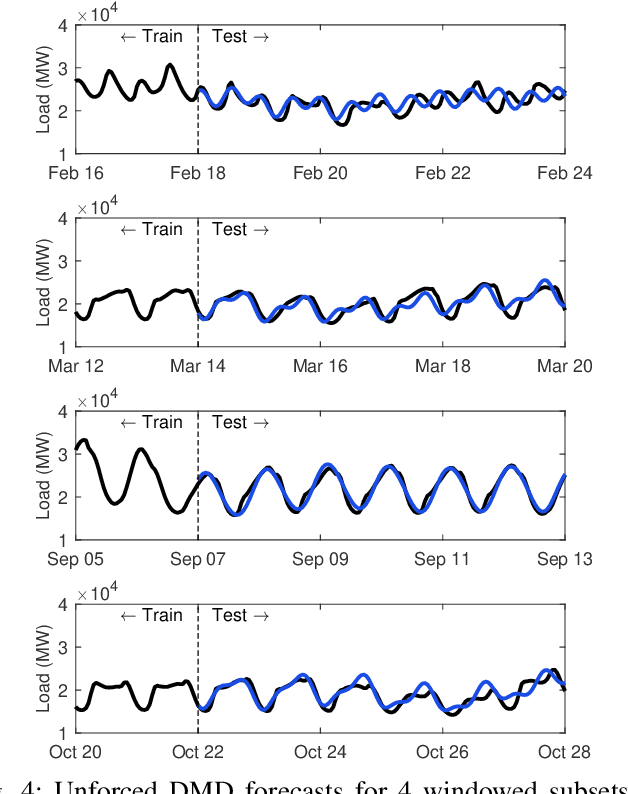
Time series forecasting remains a central challenge problem in almost all scientific disciplines, including load modeling in power systems engineering. The ability to produce accurate forecasts has major implications for real-time control, pricing, maintenance, and security decisions. We introduce a novel load forecasting method in which observed dynamics are modeled as a forced linear system using Dynamic Mode Decomposition (DMD) in time delay coordinates. Central to this approach is the insight that grid load, like many observables on complex real-world systems, has an "almost-periodic" character, i.e., a continuous Fourier spectrum punctuated by dominant peaks, which capture regular (e.g., daily or weekly) recurrences in the dynamics. The forecasting method presented takes advantage of this property by (i) regressing to a deterministic linear model whose eigenspectrum maps onto those peaks, and (ii) simultaneously learning a stochastic Gaussian process regression (GPR) process to actuate this system. Our forecasting algorithm is compared against state-of-the-art forecasting techniques not using additional explanatory variables and is shown to produce superior performance. Moreover, its use of linear intrinsic dynamics offers a number of desirable properties in terms of interpretability and parsimony.

Highly-scalable, physics-informed GANs for learning solutions of stochastic PDEs

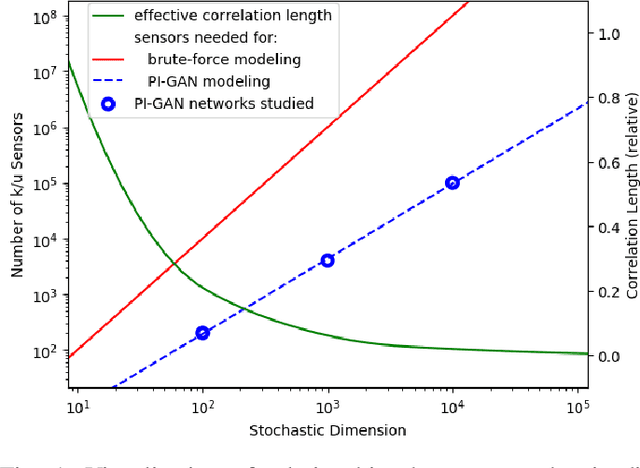
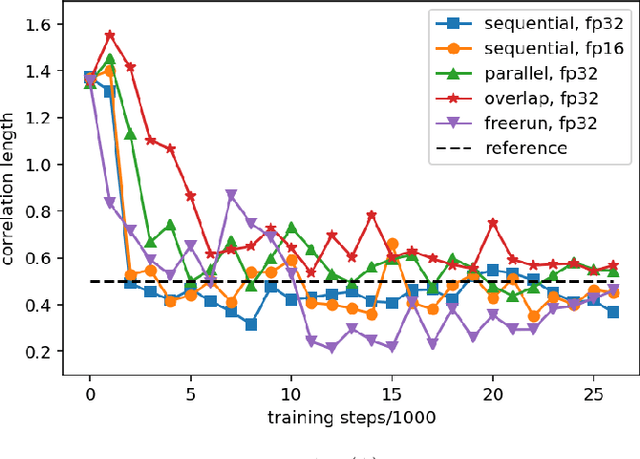
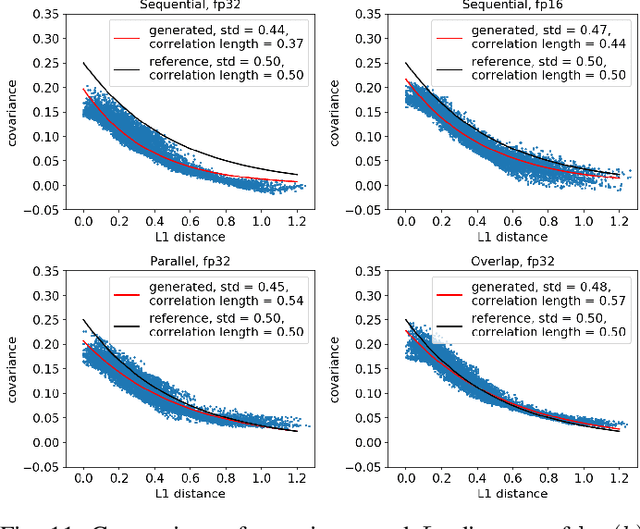
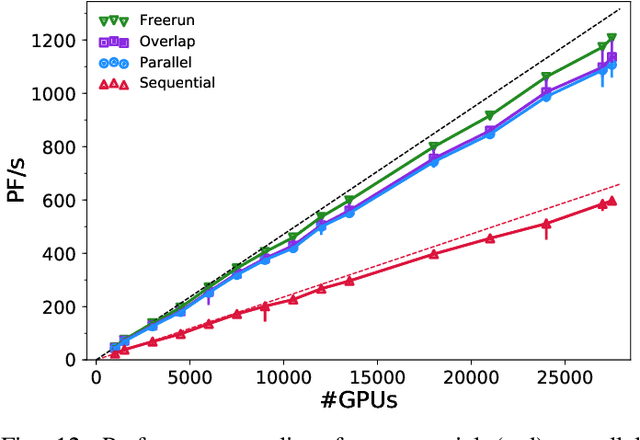
Uncertainty quantification for forward and inverse problems is a central challenge across physical and biomedical disciplines. We address this challenge for the problem of modeling subsurface flow at the Hanford Site by combining stochastic computational models with observational data using physics-informed GAN models. The geographic extent, spatial heterogeneity, and multiple correlation length scales of the Hanford Site require training a computationally intensive GAN model to thousands of dimensions. We develop a hierarchical scheme for exploiting domain parallelism, map discriminators and generators to multiple GPUs, and employ efficient communication schemes to ensure training stability and convergence. We developed a highly optimized implementation of this scheme that scales to 27,500 NVIDIA Volta GPUs and 4584 nodes on the Summit supercomputer with a 93.1% scaling efficiency, achieving peak and sustained half-precision rates of 1228 PF/s and 1207 PF/s.

Electric Load and Power Forecasting Using Ensemble Gaussian Process Regression

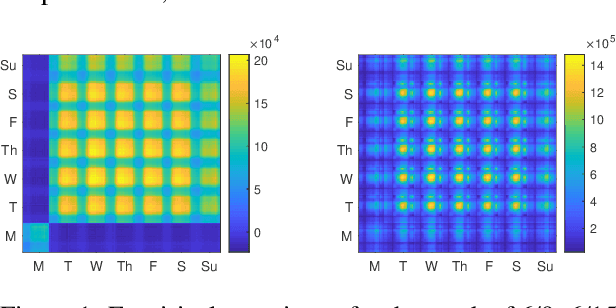
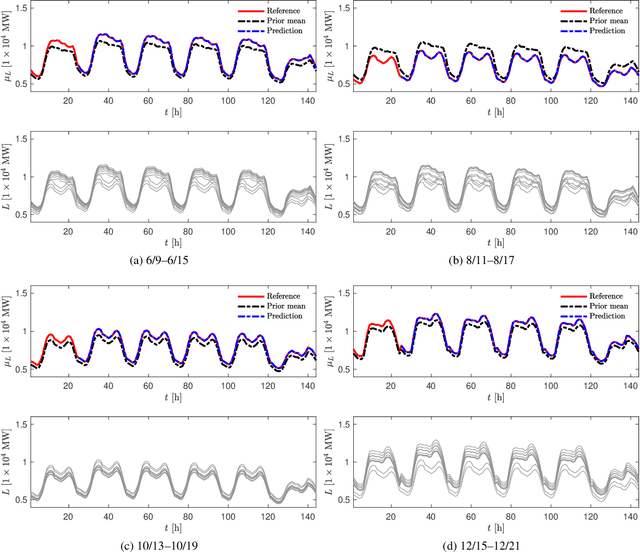
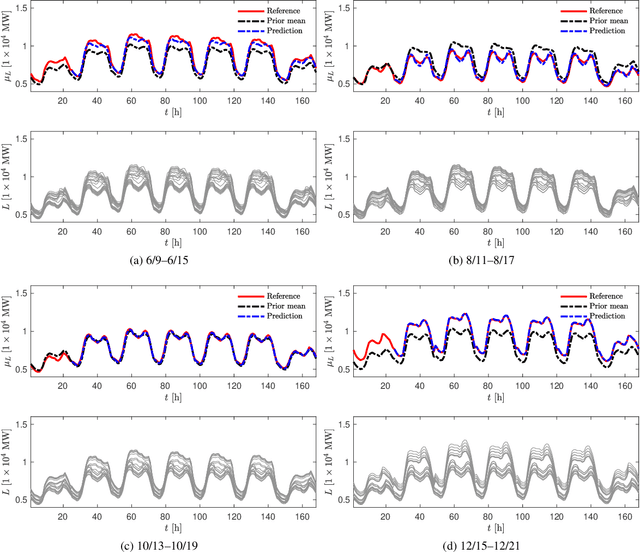
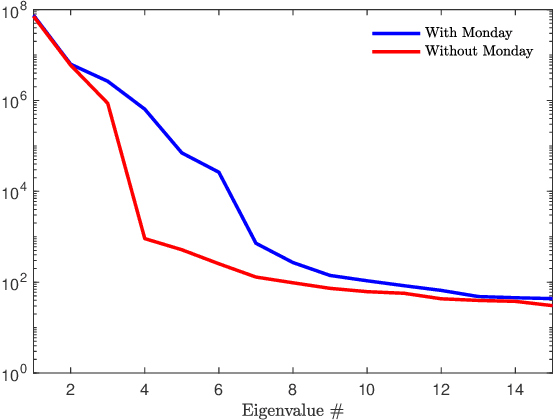
We propose a new forecasting method for predicting load demand and generation scheduling. Accurate week-long forecasting of load demand and optimal power generation is critical for efficient operation of power grid systems. In this work, we use a synthetic data set describing a power grid with 700 buses and 134 generators over a 365-days period with data synthetically generated at an hourly rate. The proposed approach for week-long forecasting is based on the Gaussian process regression (GPR) method, with prior covariance matrices of the quantities of interest (QoI) computed from ensembles formed by up to twenty preceding weeks of QoI observations. Then, we use these covariances within the GPR framework to forecast the QoIs for the following week. We demonstrate that the the proposed ensemble GPR (EGPR) method is capable of accurately forecasting weekly total load demand and power generation profiles. The EGPR method is shown to outperform traditional forecasting methods including the standard GPR and autoregressive integrated moving average (ARIMA) methods.

Physics-Informed CoKriging: A Gaussian-Process-Regression-Based Multifidelity Method for Data-Model Convergence

In this work, we propose a new Gaussian process regression (GPR)-based multifidelity method: physics-informed CoKriging (CoPhIK). In CoKriging-based multifidelity methods, the quantities of interest are modeled as linear combinations of multiple parameterized stationary Gaussian processes (GPs), and the hyperparameters of these GPs are estimated from data via optimization. In CoPhIK, we construct a GP representing low-fidelity data using physics-informed Kriging (PhIK), and model the discrepancy between low- and high-fidelity data using a parameterized GP with hyperparameters identified via optimization. Our approach reduces the cost of optimization for inferring hyperparameters by incorporating partial physical knowledge. We prove that the physical constraints in the form of deterministic linear operators are satisfied up to an error bound. Furthermore, we combine CoPhIK with a greedy active learning algorithm for guiding the selection of additional observation locations. The efficiency and accuracy of CoPhIK are demonstrated for reconstructing the partially observed modified Branin function, reconstructing the sparsely observed state of a steady state heat transport problem, and learning a conservative tracer distribution from sparse tracer concentration measurements.