Beyond validation loss: Clinically-tailored optimization metrics improve a model's clinical performance

A key task in ML is to optimize models at various stages, e.g. by choosing hyperparameters or picking a stopping point. A traditional ML approach is to use validation loss, i.e. to apply the training loss function on a validation set to guide these optimizations. However, ML for healthcare has a distinct goal from traditional ML: Models must perform well relative to specific clinical requirements, vs. relative to the loss function used for training. These clinical requirements can be captured more precisely by tailored metrics. Since many optimization tasks do not require the driving metric to be differentiable, they allow a wider range of options, including the use of metrics tailored to be clinically-relevant. In this paper we describe two controlled experiments which show how the use of clinically-tailored metrics provide superior model optimization compared to validation loss, in the sense of better performance on the clinical task. The use of clinically-relevant metrics for optimization entails some extra effort, to define the metrics and to code them into the pipeline. But it can yield models that better meet the central goal of ML for healthcare: strong performance in the clinic.

Extraction of instantaneous frequencies and amplitudes in nonstationary time-series data

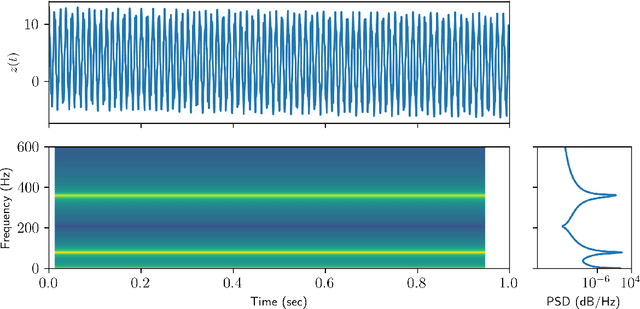
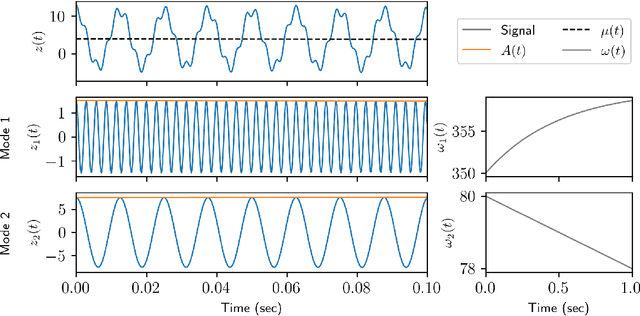
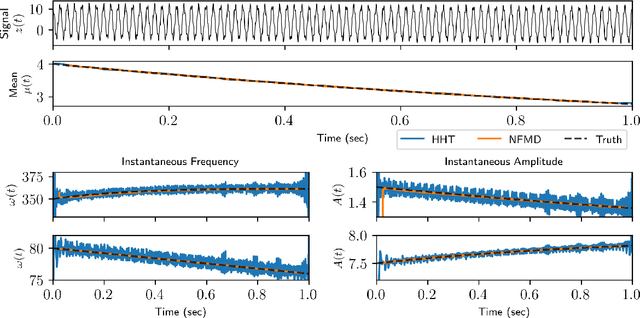
Time-series analysis is critical for a diversity of applications in science and engineering. By leveraging the strengths of modern gradient descent algorithms, the Fourier transform, multi-resolution analysis, and Bayesian spectral analysis, we propose a data-driven approach to time-frequency analysis that circumvents many of the shortcomings of classic approaches, including the extraction of nonstationary signals with discontinuities in their behavior. The method introduced is equivalent to a {\em nonstationary Fourier mode decomposition} (NFMD) for nonstationary and nonlinear temporal signals, allowing for the accurate identification of instantaneous frequencies and their amplitudes. The method is demonstrated on a diversity of time-series data, including on data from cantilever-based electrostatic force microscopy to quantify the time-dependent evolution of charging dynamics at the nanoscale.

DeepGreen: Deep Learning of Green's Functions for Nonlinear Boundary Value Problems

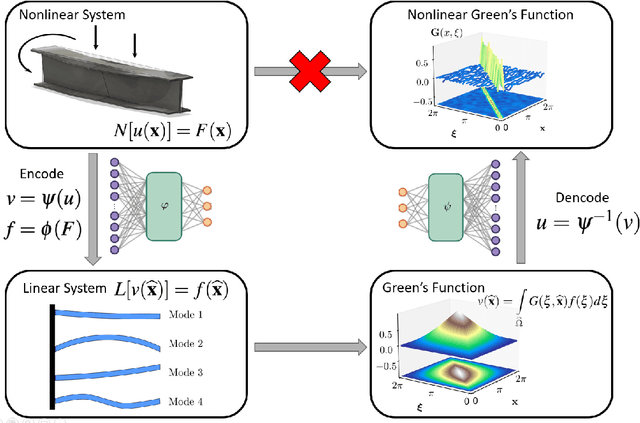
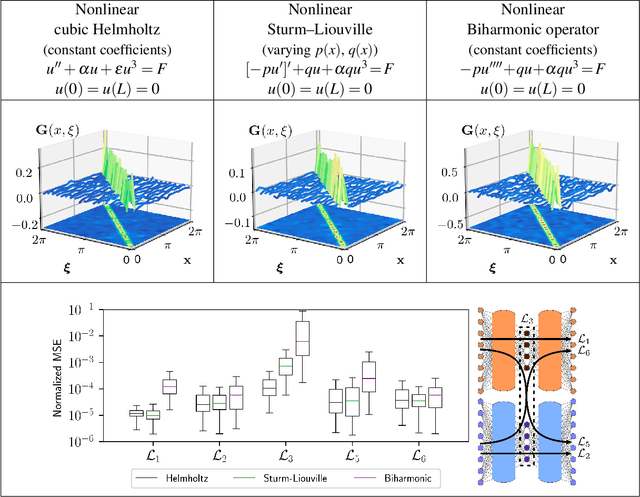
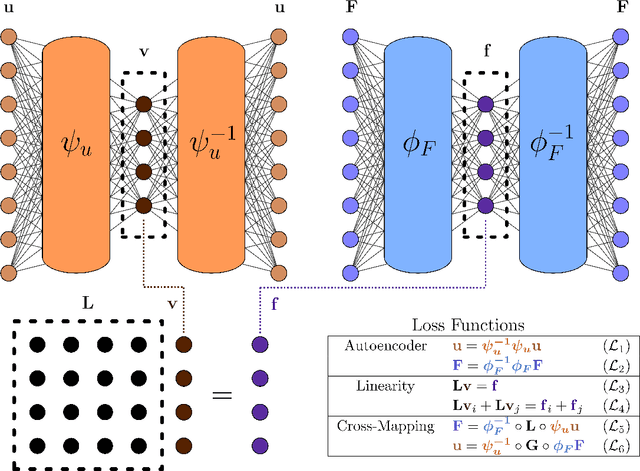
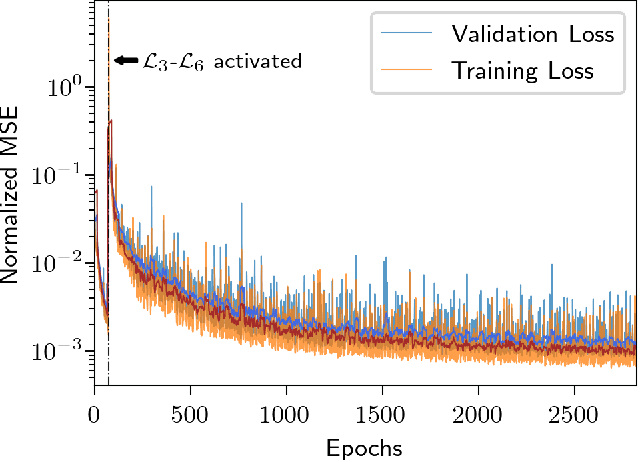
Boundary value problems (BVPs) play a central role in the mathematical analysis of constrained physical systems subjected to external forces. Consequently, BVPs frequently emerge in nearly every engineering discipline and span problem domains including fluid mechanics, electromagnetics, quantum mechanics, and elasticity. The fundamental solution, or Green's function, is a leading method for solving linear BVPs that enables facile computation of new solutions to systems under any external forcing. However, fundamental Green's function solutions for nonlinear BVPs are not feasible since linear superposition no longer holds. In this work, we propose a flexible deep learning approach to solve nonlinear BVPs using a dual-autoencoder architecture. The autoencoders discover an invertible coordinate transform that linearizes the nonlinear BVP and identifies both a linear operator $L$ and Green's function $G$ which can be used to solve new nonlinear BVPs. We find that the method succeeds on a variety of nonlinear systems including nonlinear Helmholtz and Sturm--Liouville problems, nonlinear elasticity, and a 2D nonlinear Poisson equation. The method merges the strengths of the universal approximation capabilities of deep learning with the physics knowledge of Green's functions to yield a flexible tool for identifying fundamental solutions to a variety of nonlinear systems.