Robust, High-Rate Trajectory Tracking on Insect-Scale Soft-Actuated Aerial Robots with Deep-Learned Tube MPC

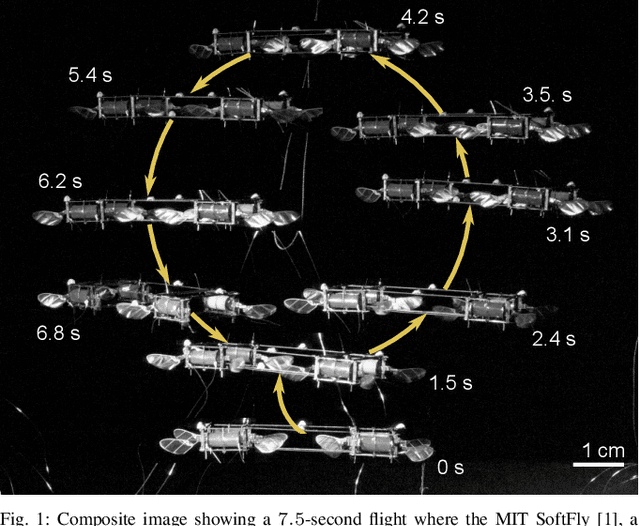
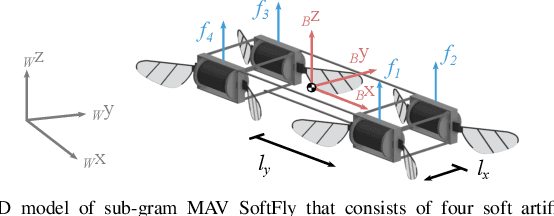
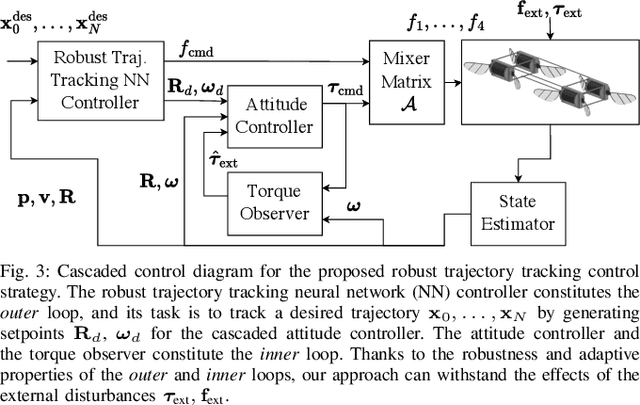
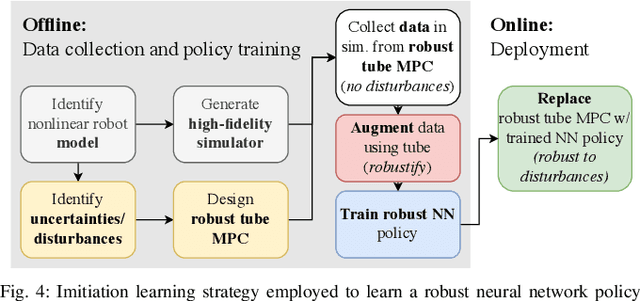
Accurate and agile trajectory tracking in sub-gram Micro Aerial Vehicles (MAVs) is challenging, as the small scale of the robot induces large model uncertainties, demanding robust feedback controllers, while the fast dynamics and computational constraints prevent the deployment of computationally expensive strategies. In this work, we present an approach for agile and computationally efficient trajectory tracking on the MIT SoftFly, a sub-gram MAV (0.7 grams). Our strategy employs a cascaded control scheme, where an adaptive attitude controller is combined with a neural network policy trained to imitate a trajectory tracking robust tube model predictive controller (RTMPC). The neural network policy is obtained using our recent work, which enables the policy to preserve the robustness of RTMPC, but at a fraction of its computational cost. We experimentally evaluate our approach, achieving position Root Mean Square Errors lower than 1.8 cm even in the more challenging maneuvers, obtaining a 60% reduction in maximum position error compared to our previous work, and demonstrating robustness to large external disturbances

Koopman-theoretic Approach for Identification of Exogenous Anomalies in Nonstationary Time-series Data

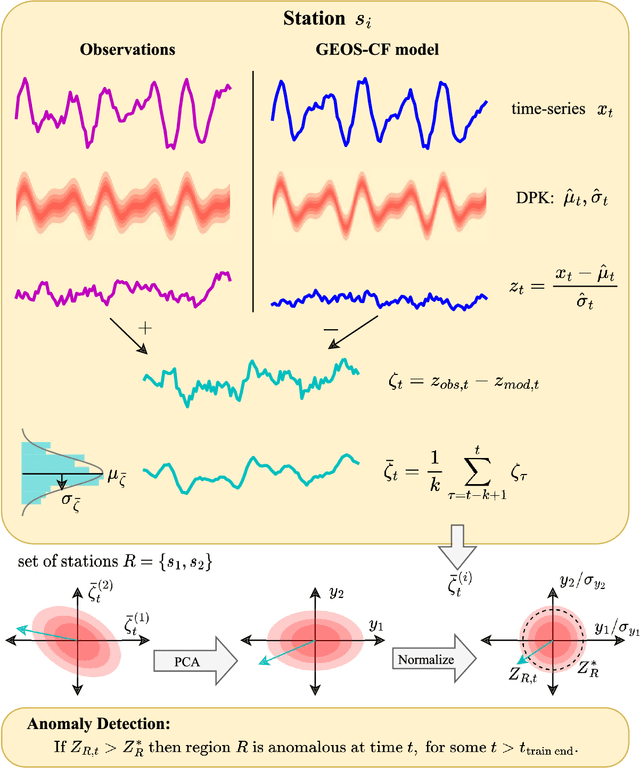
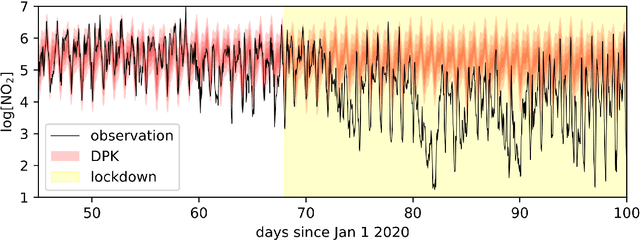
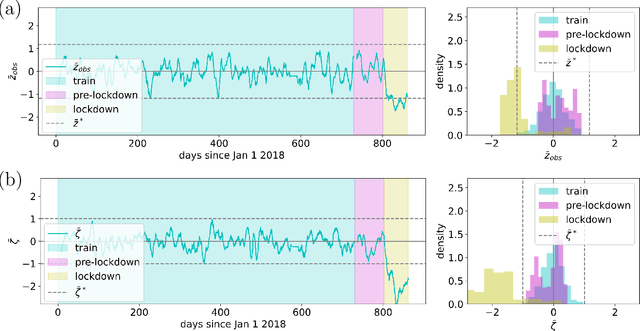
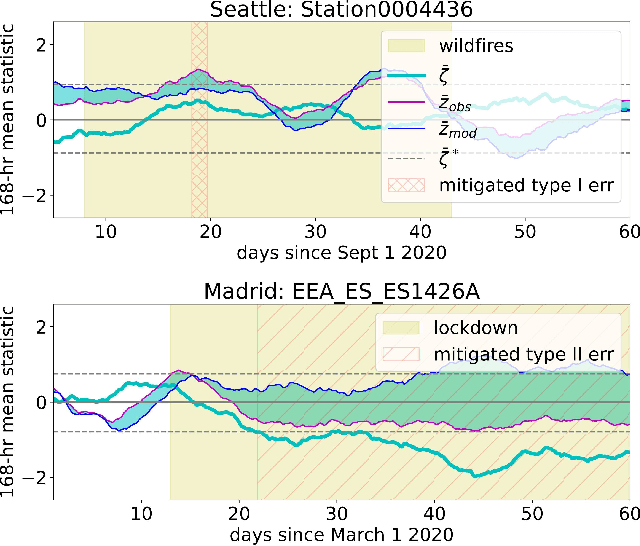
In many scenarios, it is necessary to monitor a complex system via a time-series of observations and determine when anomalous exogenous events have occurred so that relevant actions can be taken. Determining whether current observations are abnormal is challenging. It requires learning an extrapolative probabilistic model of the dynamics from historical data, and using a limited number of current observations to make a classification. We leverage recent advances in long-term probabilistic forecasting, namely {\em Deep Probabilistic Koopman}, to build a general method for classifying anomalies in multi-dimensional time-series data. We also show how to utilize models with domain knowledge of the dynamics to reduce type I and type II error. We demonstrate our proposed method on the important real-world task of global atmospheric pollution monitoring, integrating it with NASA's Global Earth System Model. The system successfully detects localized anomalies in air quality due to events such as COVID-19 lockdowns and wildfires.

The Experimental Multi-Arm Pendulum on a Cart: A Benchmark System for Chaos, Learning, and Control

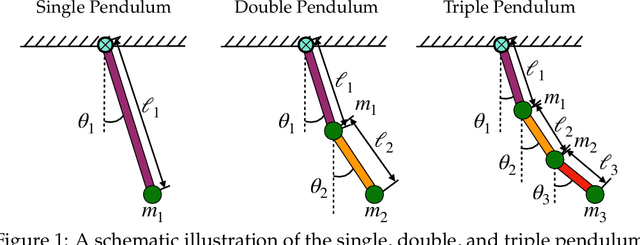
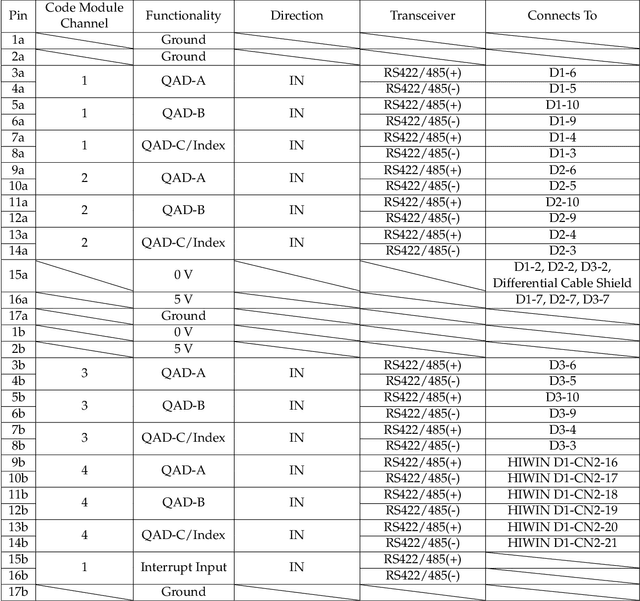
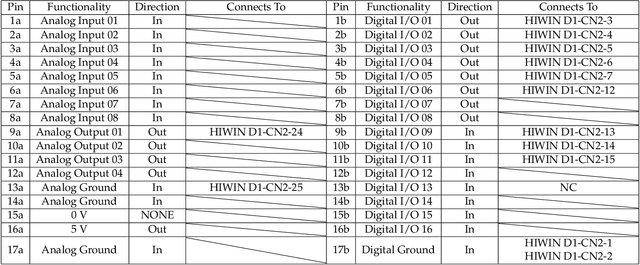
The single, double, and triple pendulum has served as an illustrative experimental benchmark system for scientists to study dynamical behavior for more than four centuries. The pendulum system exhibits a wide range of interesting behaviors, from simple harmonic motion in the single pendulum to chaotic dynamics in multi-arm pendulums. Under forcing, even the single pendulum may exhibit chaos, providing a simple example of a damped-driven system. All multi-armed pendulums are characterized by the existence of index-one saddle points, which mediate the transport of trajectories in the system, providing a simple mechanical analog of various complex transport phenomena, from biolocomotion to transport within the solar system. Further, pendulum systems have long been used to design and test both linear and nonlinear control strategies, with the addition of more arms making the problem more challenging. In this work, we provide extensive designs for the construction and operation of a high-performance, multi-link pendulum on a cart system. Although many experimental setups have been built to study the behavior of pendulum systems, such an extensive documentation on the design, construction, and operation is missing from the literature. The resulting experimental system is highly flexible, enabling a wide range of benchmark problems in dynamical systems modeling, system identification and learning, and control. To promote reproducible research, we have made our entire system open-source, including 3D CAD drawings, basic tutorial code, and data. Moreover, we discuss the possibility of extending our system capability to be operated remotely to enable researchers all around the world to use it, thus increasing access.

Neural Implicit Flow: a mesh-agnostic dimensionality reduction paradigm of spatio-temporal data

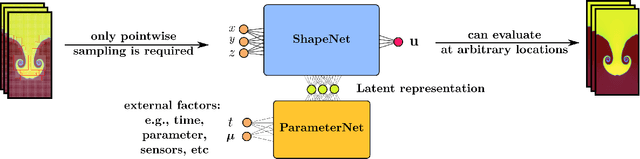
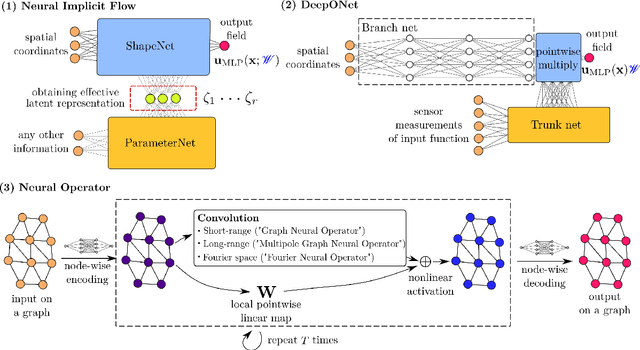
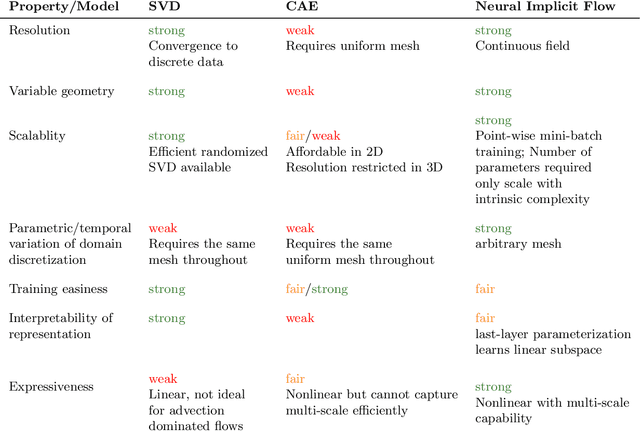
High-dimensional spatio-temporal dynamics can often be encoded in a low-dimensional subspace. Engineering applications for modeling, characterization, design, and control of such large-scale systems often rely on dimensionality reduction to make solutions computationally tractable in real-time. Common existing paradigms for dimensionality reduction include linear methods, such as the singular value decomposition (SVD), and nonlinear methods, such as variants of convolutional autoencoders (CAE). However, these encoding techniques lack the ability to efficiently represent the complexity associated with spatio-temporal data, which often requires variable geometry, non-uniform grid resolution, adaptive meshing, and/or parametric dependencies. To resolve these practical engineering challenges, we propose a general framework called Neural Implicit Flow (NIF) that enables a mesh-agnostic, low-rank representation of large-scale, parametric, spatial-temporal data. NIF consists of two modified multilayer perceptrons (MLPs): (i) ShapeNet, which isolates and represents the spatial complexity, and (ii) ParameterNet, which accounts for any other input complexity, including parametric dependencies, time, and sensor measurements. We demonstrate the utility of NIF for parametric surrogate modeling, enabling the interpretable representation and compression of complex spatio-temporal dynamics, efficient many-spatial-query tasks, and improved generalization performance for sparse reconstruction.

Discrepancy Modeling Framework: Learning missing physics, modeling systematic residuals, and disambiguating between deterministic and random effects

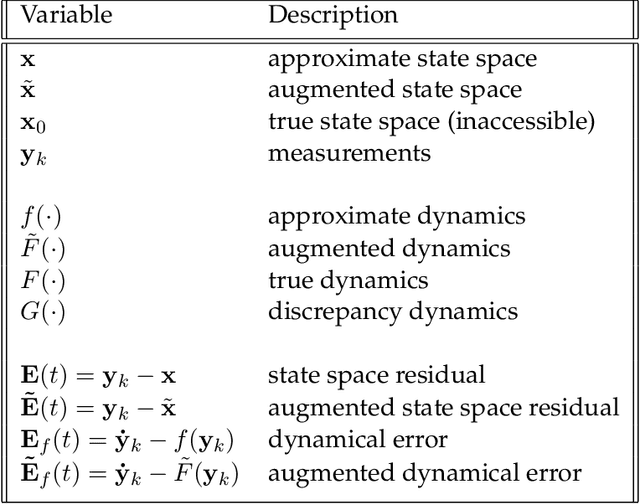
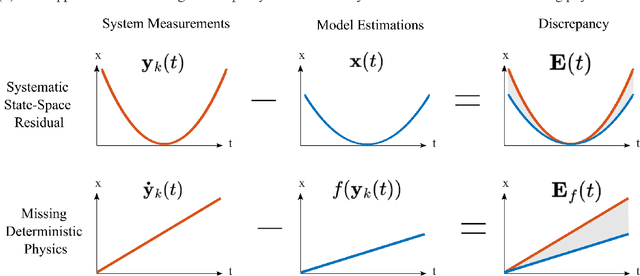
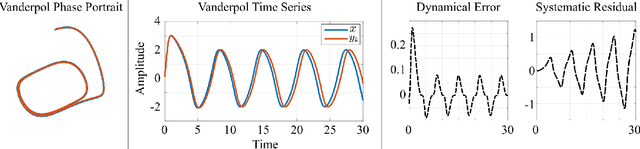
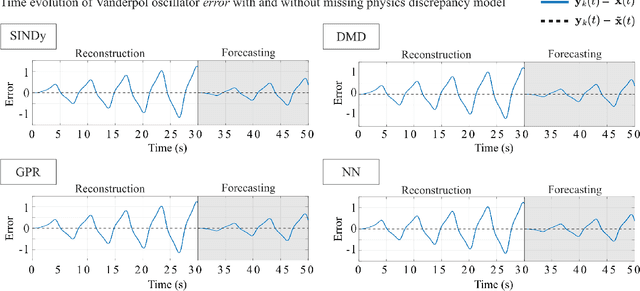
Physics-based and first-principles models pervade the engineering and physical sciences, allowing for the ability to model the dynamics of complex systems with a prescribed accuracy. The approximations used in deriving governing equations often result in discrepancies between the model and sensor-based measurements of the system, revealing the approximate nature of the equations and/or the signal-to-noise ratio of the sensor itself. In modern dynamical systems, such discrepancies between model and measurement can lead to poor quantification, often undermining the ability to produce accurate and precise control algorithms. We introduce a discrepancy modeling framework to resolve deterministic model-measurement mismatch with two distinct approaches: (i) by learning a model for the evolution of systematic state-space residual, and (ii) by discovering a model for the missing deterministic physics. Regardless of approach, a common suite of data-driven model discovery methods can be used. Specifically, we use four fundamentally different methods to demonstrate the mathematical implementations of discrepancy modeling: (i) the sparse identification of nonlinear dynamics (SINDy), (ii) dynamic mode decomposition (DMD), (iii) Gaussian process regression (GPR), and (iv) neural networks (NN). The choice of method depends on one's intent for discrepancy modeling, as well as quantity and quality of the sensor measurements. We demonstrate the utility and suitability for both discrepancy modeling approaches using the suite of data-driven modeling methods on three dynamical systems under varying signal-to-noise ratios. We compare reconstruction and forecasting accuracies and provide detailed comparatives, allowing one to select the appropriate approach and method in practice.

Dimensionally Consistent Learning with Buckingham Pi

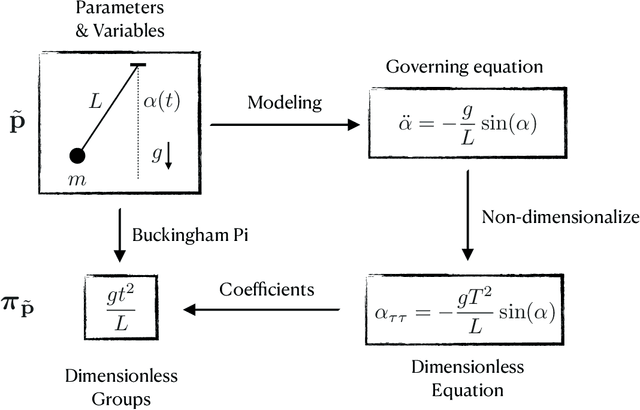
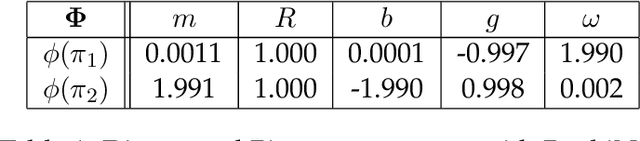
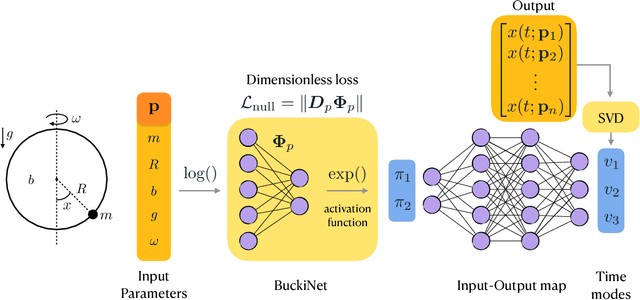
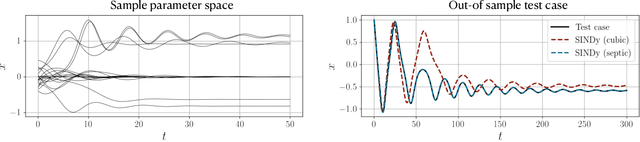
In the absence of governing equations, dimensional analysis is a robust technique for extracting insights and finding symmetries in physical systems. Given measurement variables and parameters, the Buckingham Pi theorem provides a procedure for finding a set of dimensionless groups that spans the solution space, although this set is not unique. We propose an automated approach using the symmetric and self-similar structure of available measurement data to discover the dimensionless groups that best collapse this data to a lower dimensional space according to an optimal fit. We develop three data-driven techniques that use the Buckingham Pi theorem as a constraint: (i) a constrained optimization problem with a non-parametric input-output fitting function, (ii) a deep learning algorithm (BuckiNet) that projects the input parameter space to a lower dimension in the first layer, and (iii) a technique based on sparse identification of nonlinear dynamics (SINDy) to discover dimensionless equations whose coefficients parameterize the dynamics. We explore the accuracy, robustness and computational complexity of these methods as applied to three example problems: a bead on a rotating hoop, a laminar boundary layer, and Rayleigh-B\'enard convection.

Discovering Governing Equations from Partial Measurements with Deep Delay Autoencoders

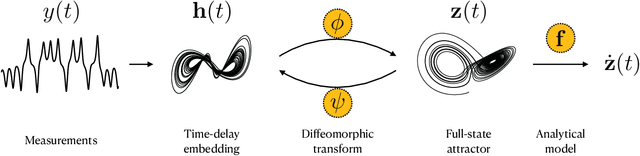
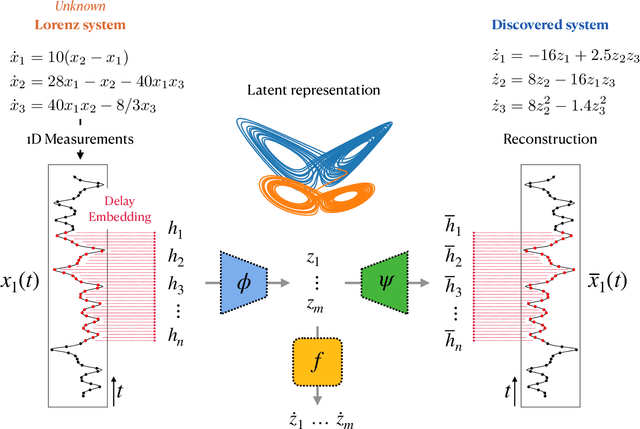
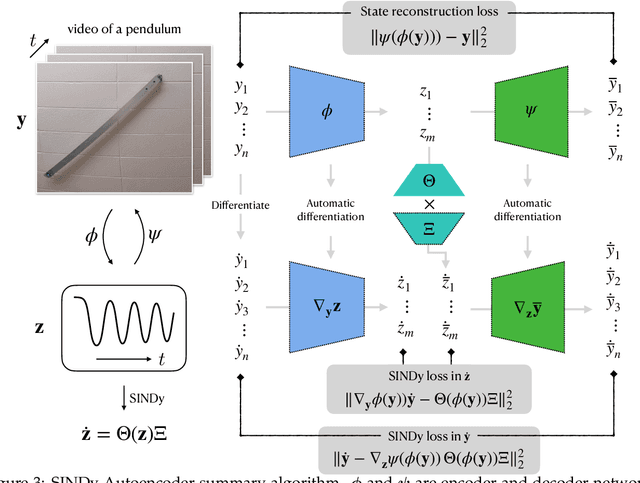
A central challenge in data-driven model discovery is the presence of hidden, or latent, variables that are not directly measured but are dynamically important. Takens' theorem provides conditions for when it is possible to augment these partial measurements with time delayed information, resulting in an attractor that is diffeomorphic to that of the original full-state system. However, the coordinate transformation back to the original attractor is typically unknown, and learning the dynamics in the embedding space has remained an open challenge for decades. Here, we design a custom deep autoencoder network to learn a coordinate transformation from the delay embedded space into a new space where it is possible to represent the dynamics in a sparse, closed form. We demonstrate this approach on the Lorenz, R\"ossler, and Lotka-Volterra systems, learning dynamics from a single measurement variable. As a challenging example, we learn a Lorenz analogue from a single scalar variable extracted from a video of a chaotic waterwheel experiment. The resulting modeling framework combines deep learning to uncover effective coordinates and the sparse identification of nonlinear dynamics (SINDy) for interpretable modeling. Thus, we show that it is possible to simultaneously learn a closed-form model and the associated coordinate system for partially observed dynamics.

PySINDy: A comprehensive Python package for robust sparse system identification

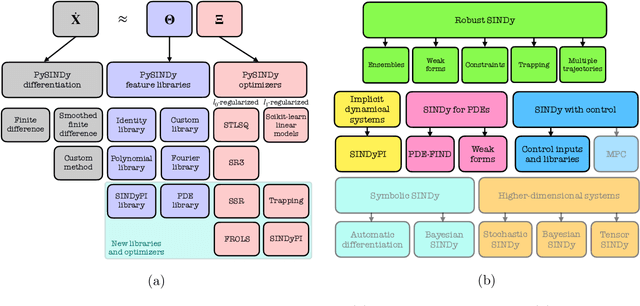
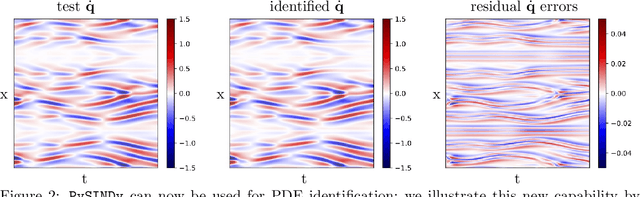
Automated data-driven modeling, the process of directly discovering the governing equations of a system from data, is increasingly being used across the scientific community. PySINDy is a Python package that provides tools for applying the sparse identification of nonlinear dynamics (SINDy) approach to data-driven model discovery. In this major update to PySINDy, we implement several advanced features that enable the discovery of more general differential equations from noisy and limited data. The library of candidate terms is extended for the identification of actuated systems, partial differential equations (PDEs), and implicit differential equations. Robust formulations, including the integral form of SINDy and ensembling techniques, are also implemented to improve performance for real-world data. Finally, we provide a range of new optimization algorithms, including several sparse regression techniques and algorithms to enforce and promote inequality constraints and stability. Together, these updates enable entirely new SINDy model discovery capabilities that have not been reported in the literature, such as constrained PDE identification and ensembling with different sparse regression optimizers.

FC2T2: The Fast Continuous Convolutional Taylor Transform with Applications in Vision and Graphics

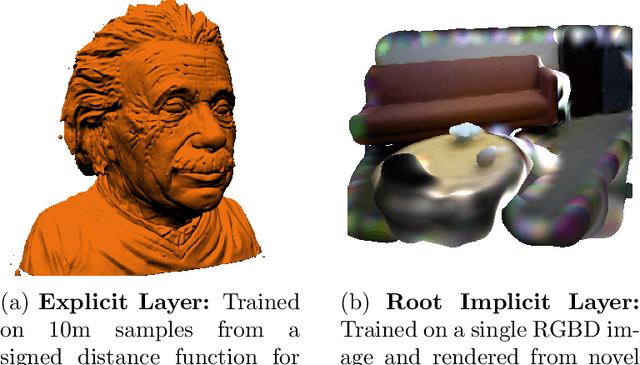
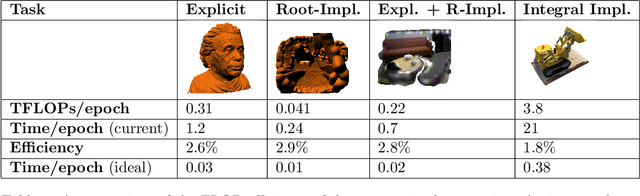
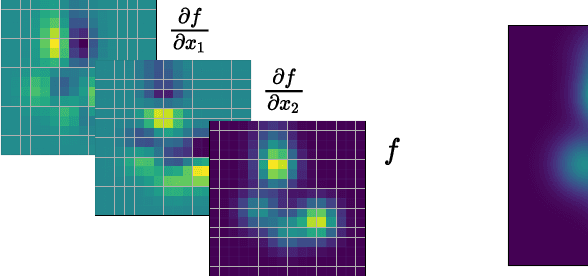
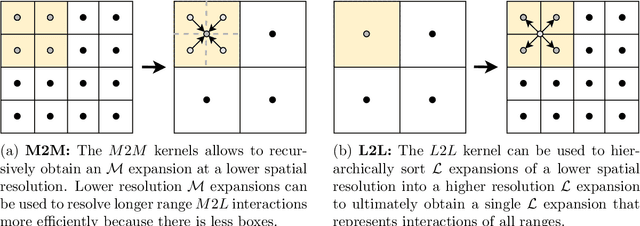
Series expansions have been a cornerstone of applied mathematics and engineering for centuries. In this paper, we revisit the Taylor series expansion from a modern Machine Learning perspective. Specifically, we introduce the Fast Continuous Convolutional Taylor Transform (FC2T2), a variant of the Fast Multipole Method (FMM), that allows for the efficient approximation of low dimensional convolutional operators in continuous space. We build upon the FMM which is an approximate algorithm that reduces the computational complexity of N-body problems from O(NM) to O(N+M) and finds application in e.g. particle simulations. As an intermediary step, the FMM produces a series expansion for every cell on a grid and we introduce algorithms that act directly upon this representation. These algorithms analytically but approximately compute the quantities required for the forward and backward pass of the backpropagation algorithm and can therefore be employed as (implicit) layers in Neural Networks. Specifically, we introduce a root-implicit layer that outputs surface normals and object distances as well as an integral-implicit layer that outputs a rendering of a radiance field given a 3D pose. In the context of Machine Learning, $N$ and $M$ can be understood as the number of model parameters and model evaluations respectively which entails that, for applications that require repeated function evaluations which are prevalent in Computer Vision and Graphics, unlike regular Neural Networks, the techniques introduce in this paper scale gracefully with parameters. For some applications, this results in a 200x reduction in FLOPs compared to state-of-the-art approaches at a reasonable or non-existent loss in accuracy.

A toolkit for data-driven discovery of governing equations in high-noise regimes

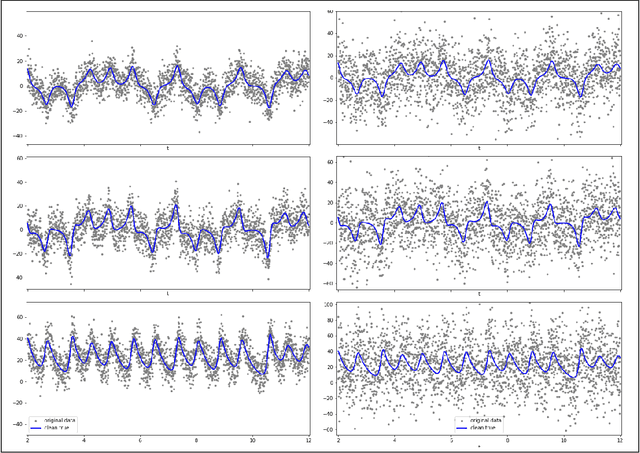
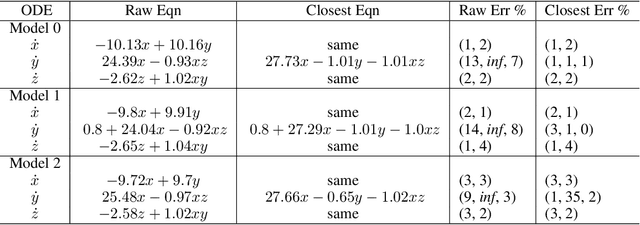
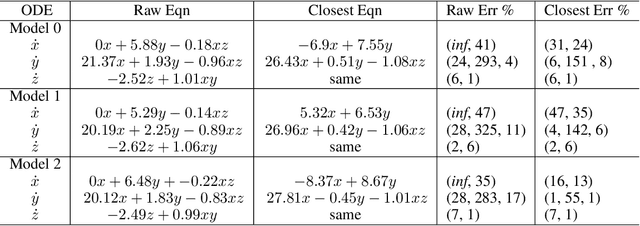
We consider the data-driven discovery of governing equations from time-series data in the limit of high noise. The algorithms developed describe an extensive toolkit of methods for circumventing the deleterious effects of noise in the context of the sparse identification of nonlinear dynamics (SINDy) framework. We offer two primary contributions, both focused on noisy data acquired from a system x' = f(x). First, we propose, for use in high-noise settings, an extensive toolkit of critically enabling extensions for the SINDy regression method, to progressively cull functionals from an over-complete library and yield a set of sparse equations that regress to the derivate x'. These innovations can extract sparse governing equations and coefficients from high-noise time-series data (e.g. 300% added noise). For example, it discovers the correct sparse libraries in the Lorenz system, with median coefficient estimate errors equal to 1% - 3% (for 50% noise), 6% - 8% (for 100% noise); and 23% - 25% (for 300% noise). The enabling modules in the toolkit are combined into a single method, but the individual modules can be tactically applied in other equation discovery methods (SINDy or not) to improve results on high-noise data. Second, we propose a technique, applicable to any model discovery method based on x' = f(x), to assess the accuracy of a discovered model in the context of non-unique solutions due to noisy data. Currently, this non-uniqueness can obscure a discovered model's accuracy and thus a discovery method's effectiveness. We describe a technique that uses linear dependencies among functionals to transform a discovered model into an equivalent form that is closest to the true model, enabling more accurate assessment of a discovered model's accuracy.