Machine Learning Accelerated Likelihood-Free Event Reconstruction in Dark Matter Direct Detection

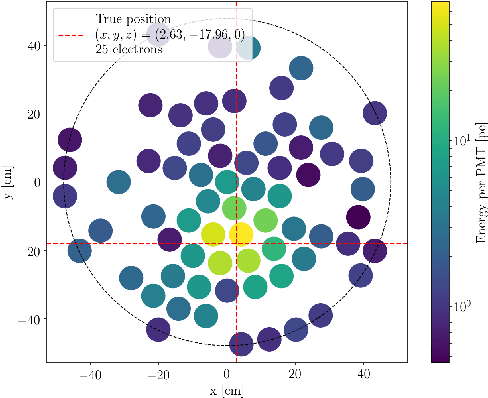
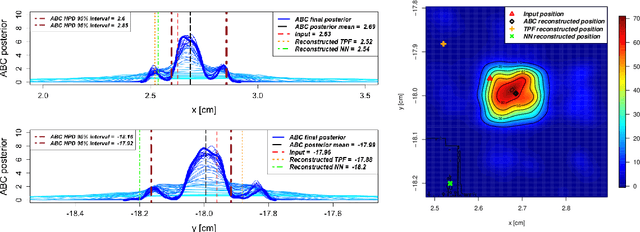
Reconstructing the position of an interaction for any dual-phase time projection chamber (TPC) with the best precision is key to directly detect Dark Matter. Using the likelihood-free framework, a new algorithm to reconstruct the 2-D (x; y) position and the size of the charge signal (e) of an interaction is presented. The algorithm uses the charge signal (S2) light distribution obtained by simulating events using a waveform generator. To deal with the computational effort required by the likelihood-free approach, we employ the Bayesian Optimization for Likelihood-Free Inference (BOLFI) algorithm. Together with BOLFI, prior distributions for the parameters of interest (x; y; e) and highly informative discrepancy measures to perform the analyses are introduced. We evaluate the quality of the proposed algorithm by a comparison against the currently existing alternative methods using a large-scale simulation study. BOLFI provides a natural probabilistic uncertainty measure for the reconstruction and it improved the accuracy of the reconstruction over the next best algorithm by up to 15% when focusing on events over a large radii (R > 30 cm). In addition, BOLFI provides the smallest uncertainties among all the tested methods.

Layered Adaptive Importance Sampling

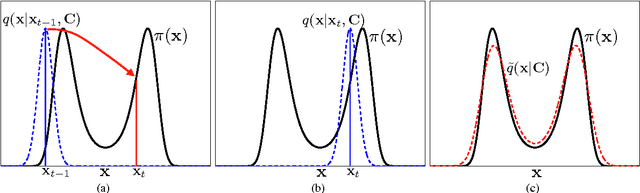
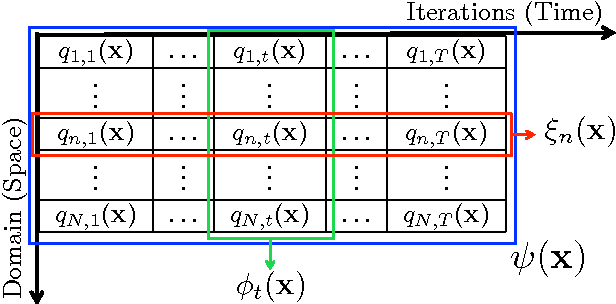
Monte Carlo methods represent the "de facto" standard for approximating complicated integrals involving multidimensional target distributions. In order to generate random realizations from the target distribution, Monte Carlo techniques use simpler proposal probability densities to draw candidate samples. The performance of any such method is strictly related to the specification of the proposal distribution, such that unfortunate choices easily wreak havoc on the resulting estimators. In this work, we introduce a layered (i.e., hierarchical) procedure to generate samples employed within a Monte Carlo scheme. This approach ensures that an appropriate equivalent proposal density is always obtained automatically (thus eliminating the risk of a catastrophic performance), although at the expense of a moderate increase in the complexity. Furthermore, we provide a general unified importance sampling (IS) framework, where multiple proposal densities are employed and several IS schemes are introduced by applying the so-called deterministic mixture approach. Finally, given these schemes, we also propose a novel class of adaptive importance samplers using a population of proposals, where the adaptation is driven by independent parallel or interacting Markov Chain Monte Carlo (MCMC) chains. The resulting algorithms efficiently combine the benefits of both IS and MCMC methods.

Orthogonal parallel MCMC methods for sampling and optimization

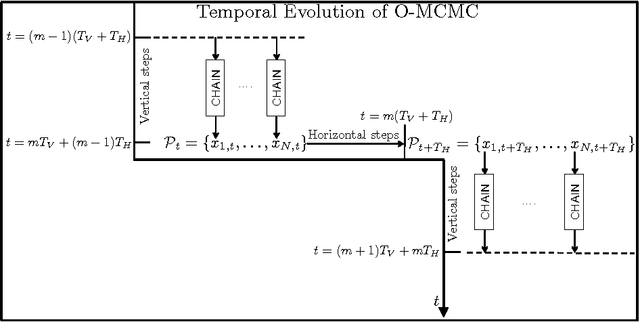
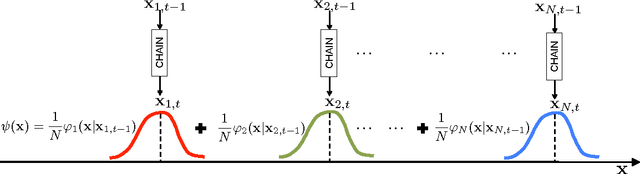
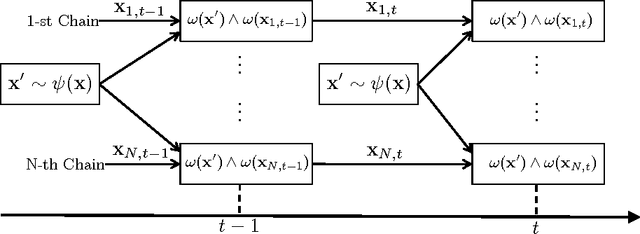
Monte Carlo (MC) methods are widely used for Bayesian inference and optimization in statistics, signal processing and machine learning. A well-known class of MC methods are Markov Chain Monte Carlo (MCMC) algorithms. In order to foster better exploration of the state space, specially in high-dimensional applications, several schemes employing multiple parallel MCMC chains have been recently introduced. In this work, we describe a novel parallel interacting MCMC scheme, called {\it orthogonal MCMC} (O-MCMC), where a set of "vertical" parallel MCMC chains share information using some "horizontal" MCMC techniques working on the entire population of current states. More specifically, the vertical chains are led by random-walk proposals, whereas the horizontal MCMC techniques employ independent proposals, thus allowing an efficient combination of global exploration and local approximation. The interaction is contained in these horizontal iterations. Within the analysis of different implementations of O-MCMC, novel schemes in order to reduce the overall computational cost of parallel multiple try Metropolis (MTM) chains are also presented. Furthermore, a modified version of O-MCMC for optimization is provided by considering parallel simulated annealing (SA) algorithms. Numerical results show the advantages of the proposed sampling scheme in terms of efficiency in the estimation, as well as robustness in terms of independence with respect to initial values and the choice of the parameters.