Twin Neural Network Regression is a Semi-Supervised Regression Algorithm

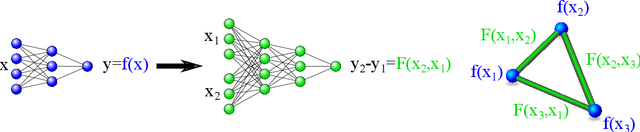
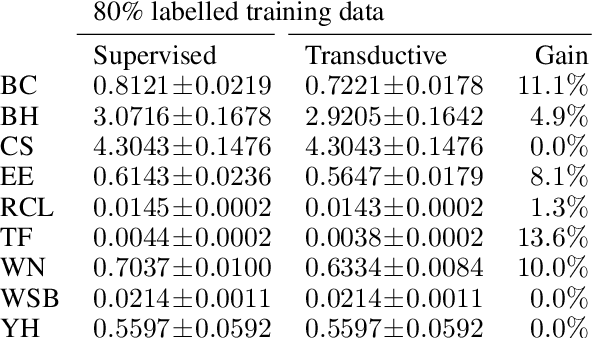
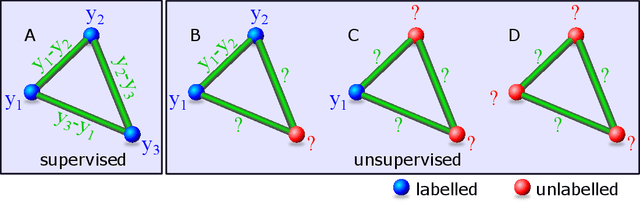
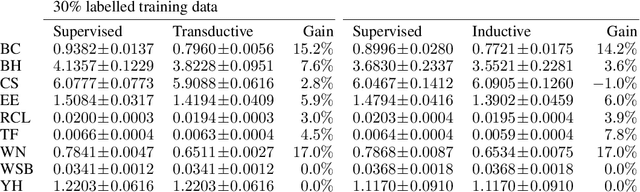
Twin neural network regression (TNNR) is a semi-supervised regression algorithm, it can be trained on unlabelled data points as long as other, labelled anchor data points, are present. TNNR is trained to predict differences between the target values of two different data points rather than the targets themselves. By ensembling predicted differences between the targets of an unseen data point and all training data points, it is possible to obtain a very accurate prediction for the original regression problem. Since any loop of predicted differences should sum to zero, loops can be supplied to the training data, even if the data points themselves within loops are unlabelled. Semi-supervised training improves TNNR performance, which is already state of the art, significantly.

Unsupervised Hyperspectral Stimulated Raman Microscopy Image Enhancement: De-Noising and Segmentation via One-Shot Deep Learning

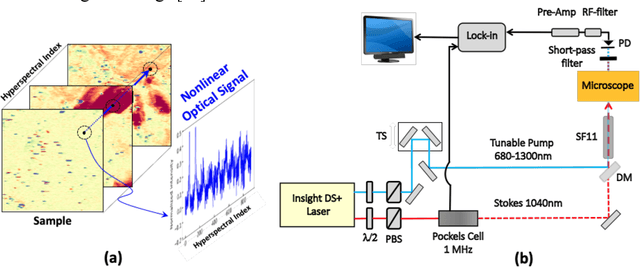
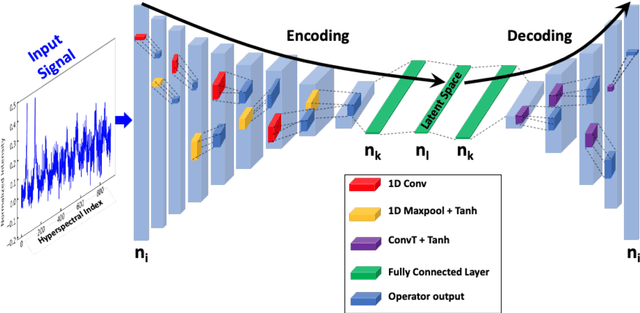
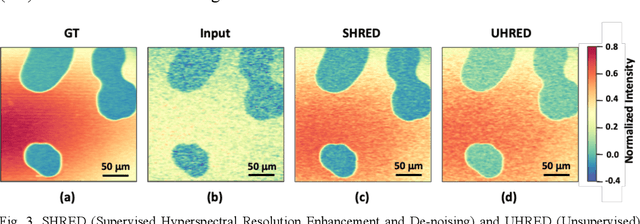
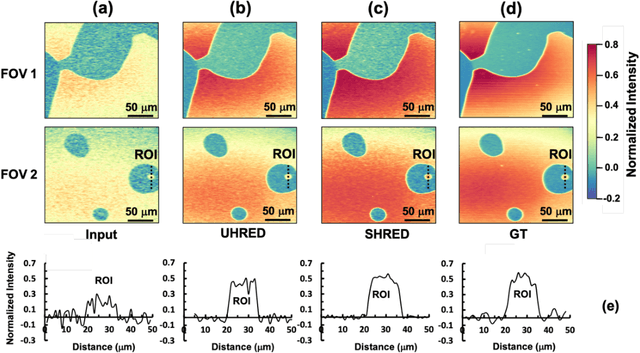
Hyperspectral stimulated Raman scattering (SRS) microscopy is a powerful label-free, chemical-specific technique for biomedical and mineralogical imaging which can suffer from low signal-to-noise ratios due to requirements of low input laser power or fast imaging, or from optical scattering and low target concentration. Here, we demonstrate a deep learning neural net model and unsupervised machine-learning algorithm for rapid and automatic de-noising and segmentation of SRS images based on a ten layer convolutional autoencoder: UHRED (Unsupervised Hyperspectral Resolution Enhancement and De-noising). UHRED is trained in an unsupervised manner using only a single (one-shot) hyperspectral image, with no requirements for training on high quality (ground truth) labelled data sets or images. Importantly, although we illustrate this method using SRS, the hyperspectral index (signal as a function of a laser parameter) may be any imaging modality such as harmonic generation, linear and/or nonlinear fluorescence, CARS, Pump-Probe, Thermal Lensing and Cross-Phase microscopy. UHRED significantly enhances SRS image contrast by de-noising the extracted Raman spectra at every image pixel. Applying a k-means clustering algorithm provides automatic, unsupervised image segmentation based on Raman vibrational spectra of the sample constituents, yielding intuitive chemical species maps, as we demonstrate for the case of a complex lithium ore sample.

Golem: An algorithm for robust experiment and process optimization

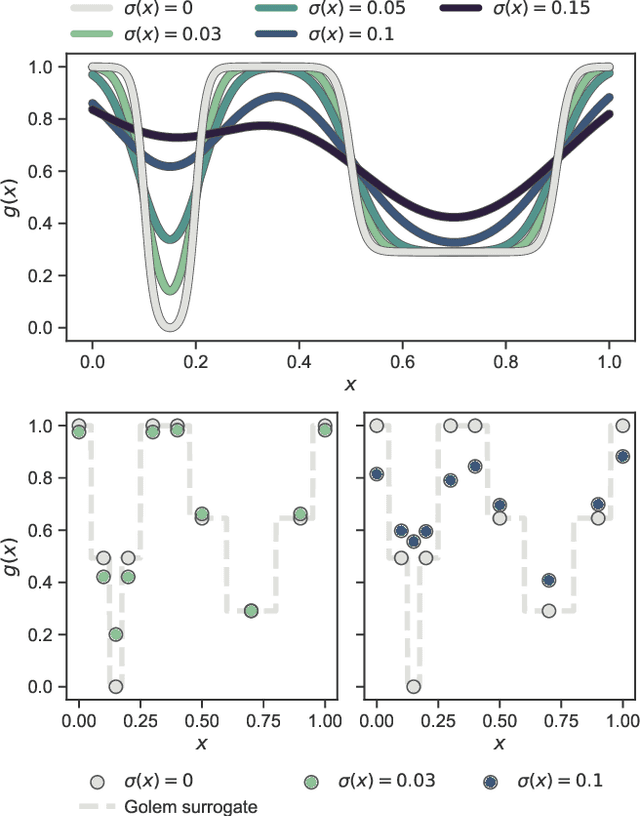
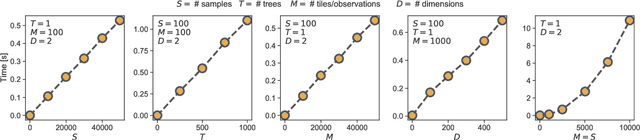
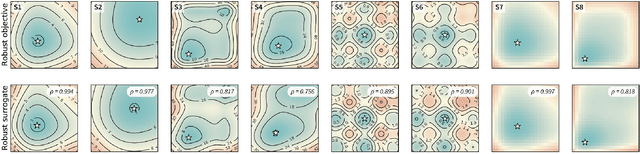
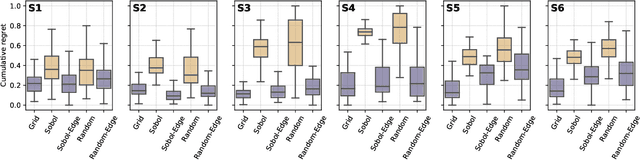
Numerous challenges in science and engineering can be framed as optimization tasks, including the maximization of reaction yields, the optimization of molecular and materials properties, and the fine-tuning of automated hardware protocols. Design of experiment and optimization algorithms are often adopted to solve these tasks efficiently. Increasingly, these experiment planning strategies are coupled with automated hardware to enable autonomous experimental platforms. The vast majority of the strategies used, however, do not consider robustness against the variability of experiment and process conditions. In fact, it is generally assumed that these parameters are exact and reproducible. Yet some experiments may have considerable noise associated with some of their conditions, and process parameters optimized under precise control may be applied in the future under variable operating conditions. In either scenario, the optimal solutions found might not be robust against input variability, affecting the reproducibility of results and returning suboptimal performance in practice. Here, we introduce Golem, an algorithm that is agnostic to the choice of experiment planning strategy and that enables robust experiment and process optimization. Golem identifies optimal solutions that are robust to input uncertainty, thus ensuring the reproducible performance of optimized experimental protocols and processes. It can be used to analyze the robustness of past experiments, or to guide experiment planning algorithms toward robust solutions on the fly. We assess the performance and domain of applicability of Golem through extensive benchmark studies and demonstrate its practical relevance by optimizing an analytical chemistry protocol under the presence of significant noise in its experimental conditions.

Weakly-supervised multi-class object localization using only object counts as labels

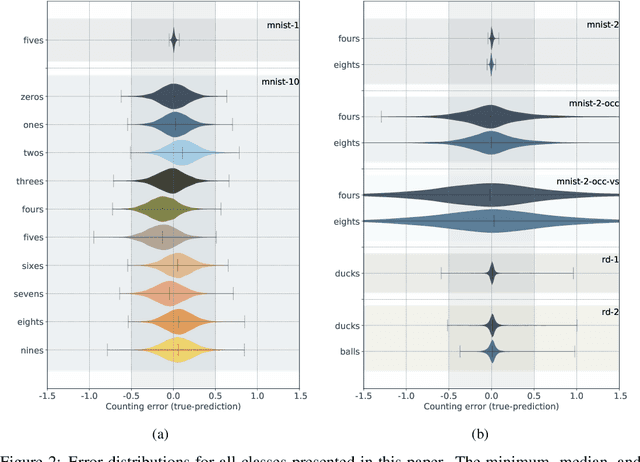
We demonstrate the use of an extensive deep neural network to localize instances of objects in images. The EDNN is naturally able to accurately perform multi-class counting using only ground truth count values as labels. Without providing any conceptual information, object annotations, or pixel segmentation information, the neural network is able to formulate its own conceptual representation of the items in the image. Using images labelled with only the counts of the objects present,the structure of the extensive deep neural network can be exploited to perform localization of the objects within the visual field. We demonstrate that a trained EDNN can be used to count objects in images much larger than those on which it was trained. In order to demonstrate our technique, we introduce seven new data sets: five progressively harder MNIST digit-counting data sets, and two datasets of 3d-rendered rubber ducks in various situations. On most of these datasets, the EDNN achieves greater than 99% test set accuracy in counting objects.

Interpretable discovery of new semiconductors with machine learning

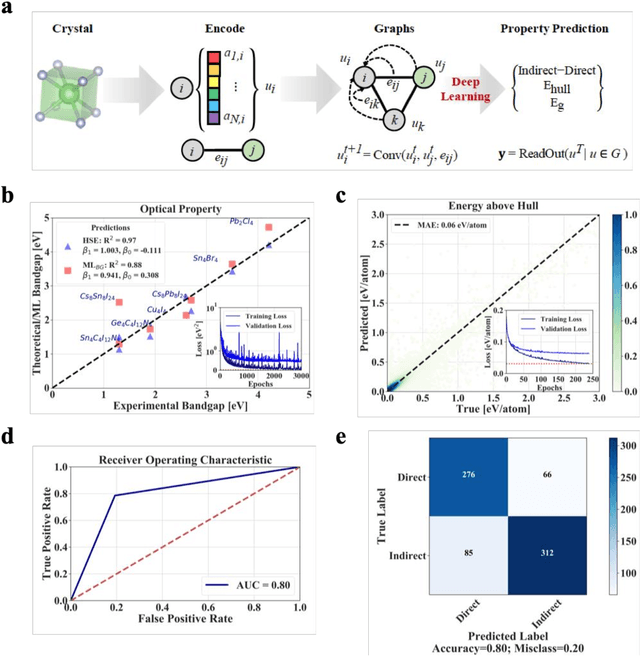
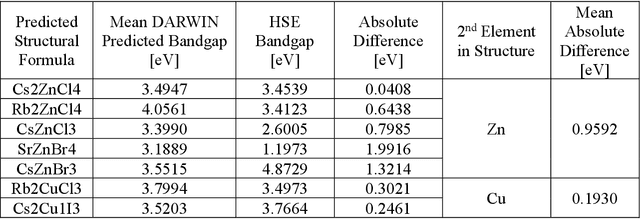
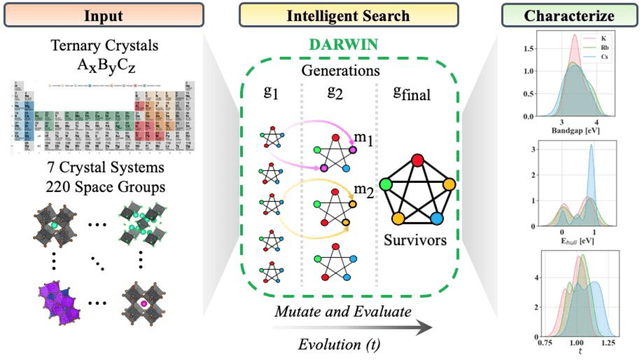
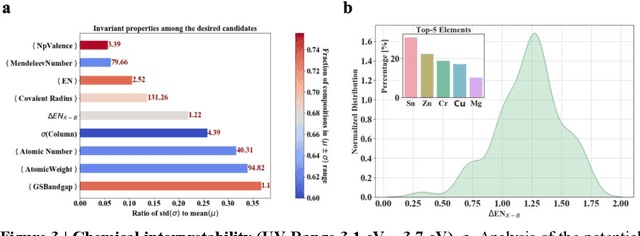
Machine learning models of materials$^{1-5}$ accelerate discovery compared to ab initio methods: deep learning models now reproduce density functional theory (DFT)-calculated results at one hundred thousandths of the cost of DFT$^{6}$. To provide guidance in experimental materials synthesis, these need to be coupled with an accurate yet effective search algorithm and training data consistent with experimental observations. Here we report an evolutionary algorithm powered search which uses machine-learned surrogate models trained on high-throughput hybrid functional DFT data benchmarked against experimental bandgaps: Deep Adaptive Regressive Weighted Intelligent Network (DARWIN). The strategy enables efficient search over the materials space of ~10$^8$ ternaries and 10$^{11}$ quaternaries$^{7}$ for candidates with target properties. It provides interpretable design rules, such as our finding that the difference in the electronegativity between the halide and B-site cation being a strong predictor of ternary structural stability. As an example, when we seek UV emission, DARWIN predicts K$_2$CuX$_3$ (X = Cl, Br) as a promising materials family, based on its electronegativity difference. We synthesized and found these materials to be stable, direct bandgap UV emitters. The approach also allows knowledge distillation for use by humans.

Twin Neural Network Regression

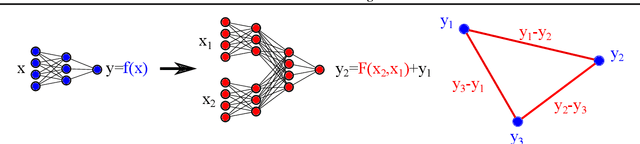
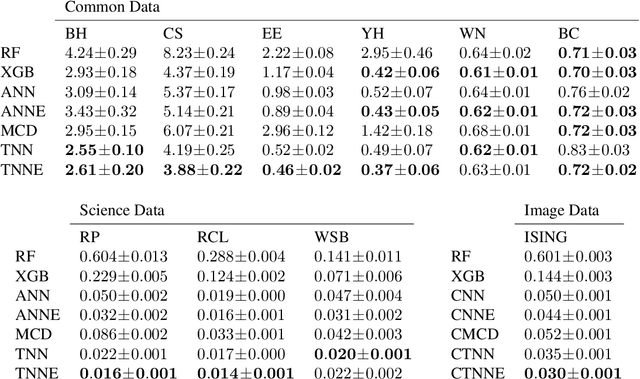
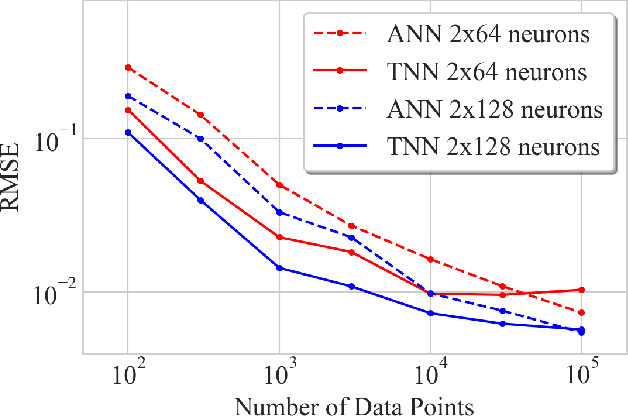
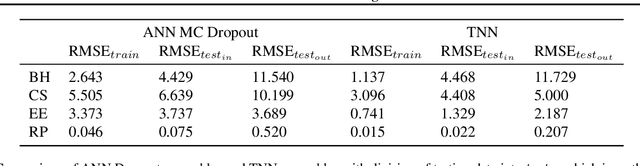
We introduce twin neural network (TNN) regression. This method predicts differences between the target values of two different data points rather than the targets themselves. The solution of a traditional regression problem is then obtained by averaging over an ensemble of all predicted differences between the targets of an unseen data point and all training data points. Whereas ensembles are normally costly to produce, TNN regression intrinsically creates an ensemble of predictions of twice the size of the training set while only training a single neural network. Since ensembles have been shown to be more accurate than single models this property naturally transfers to TNN regression. We show that TNNs are able to compete or yield more accurate predictions for different data sets, compared to other state-of-the-art methods. Furthermore, TNN regression is constrained by self-consistency conditions. We find that the violation of these conditions provides an estimate for the prediction uncertainty.

Neuroevolutionary learning of particles and protocols for self-assembly

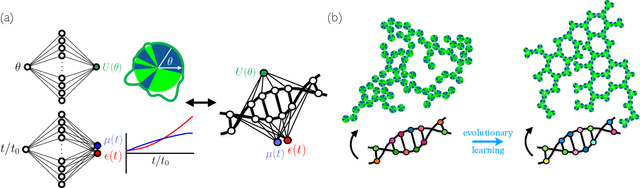
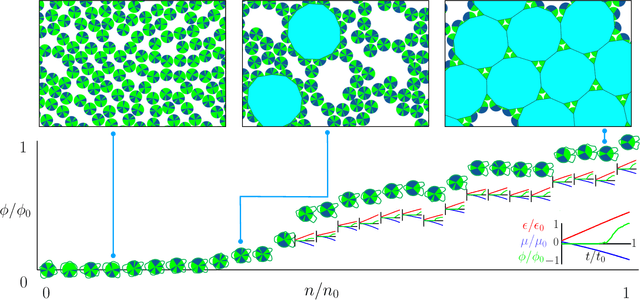
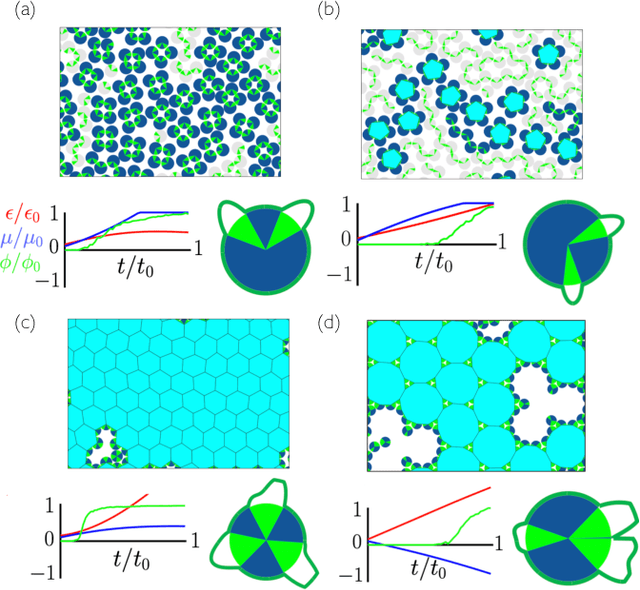
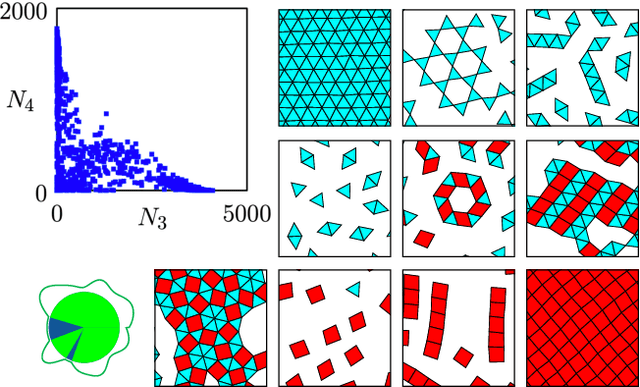
Within simulations of molecules deposited on a surface we show that neuroevolutionary learning can design particles and time-dependent protocols to promote self-assembly, without input from physical concepts such as thermal equilibrium or mechanical stability and without prior knowledge of candidate or competing structures. The learning algorithm is capable of both directed and exploratory design: it can assemble a material with a user-defined property, or search for novelty in the space of specified order parameters. In the latter mode it explores the space of what can be made rather than the space of structures that are low in energy but not necessarily kinetically accessible.

Dynamical large deviations of two-dimensional kinetically constrained models using a neural-network state ansatz

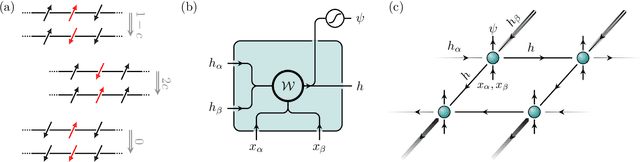
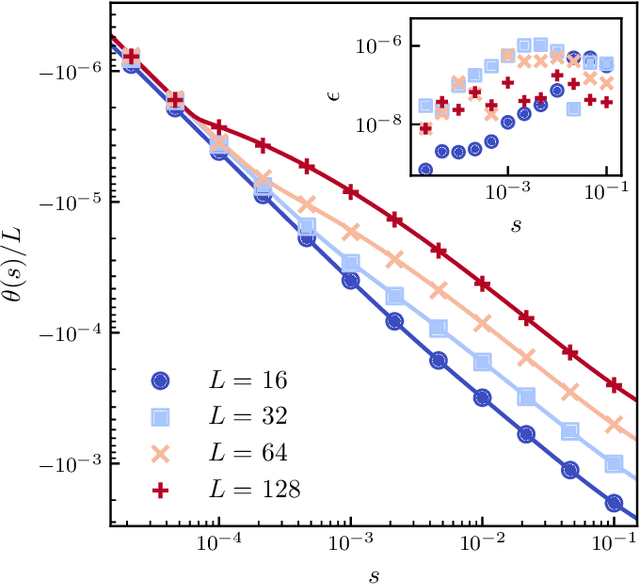
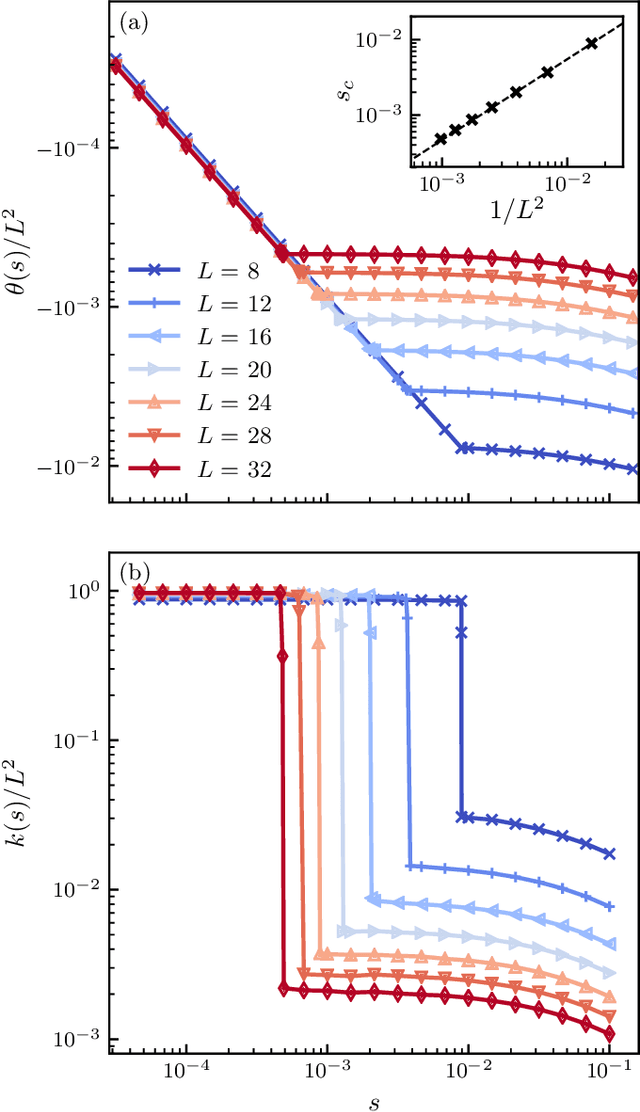
We use a neural network ansatz originally designed for the variational optimization of quantum systems to study dynamical large deviations in classical ones. We obtain the scaled cumulant-generating function for the dynamical activity of the Fredrickson-Andersen model, a prototypical kinetically constrained model, in one and two dimensions, and present the first size-scaling analysis of the dynamical activity in two dimensions. These results provide a new route to the study of dynamical large-deviation functions, and highlight the broad applicability of the neural-network state ansatz across domains in physics.

Scientific intuition inspired by machine learning generated hypotheses

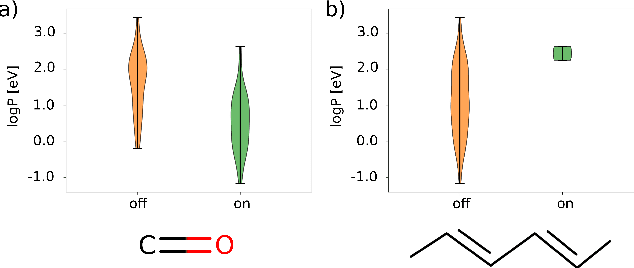
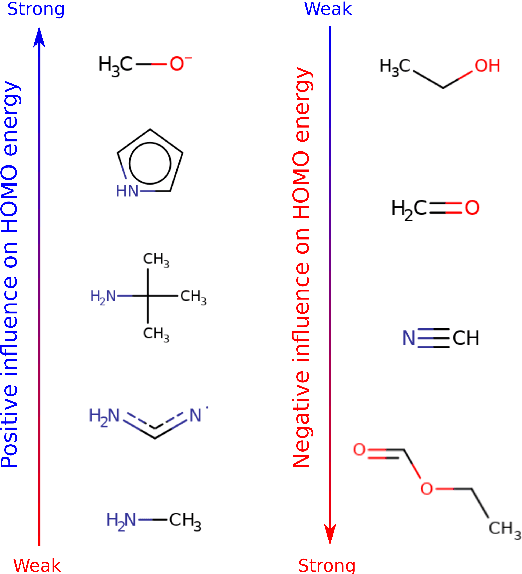
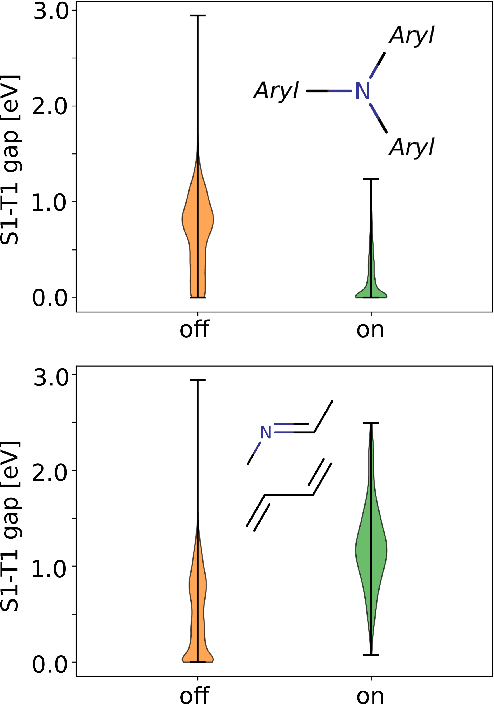
Machine learning with application to questions in the physical sciences has become a widely used tool, successfully applied to classification, regression and optimization tasks in many areas. Research focus mostly lies in improving the accuracy of the machine learning models in numerical predictions, while scientific understanding is still almost exclusively generated by human researchers analysing numerical results and drawing conclusions. In this work, we shift the focus on the insights and the knowledge obtained by the machine learning models themselves. In particular, we study how it can be extracted and used to inspire human scientists to increase their intuitions and understanding of natural systems. We apply gradient boosting in decision trees to extract human interpretable insights from big data sets from chemistry and physics. In chemistry, we not only rediscover widely know rules of thumb but also find new interesting motifs that tell us how to control solubility and energy levels of organic molecules. At the same time, in quantum physics, we gain new understanding on experiments for quantum entanglement. The ability to go beyond numerics and to enter the realm of scientific insight and hypothesis generation opens the door to use machine learning to accelerate the discovery of conceptual understanding in some of the most challenging domains of science.

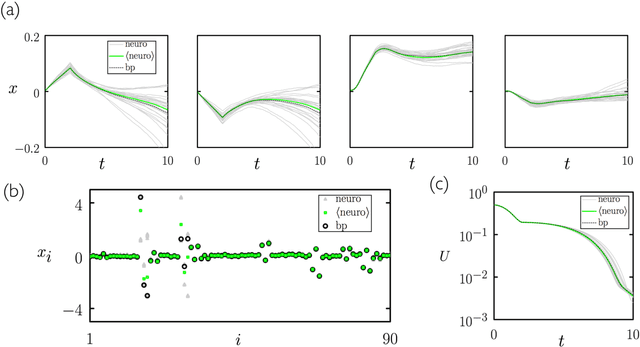
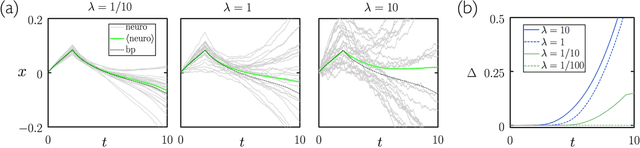
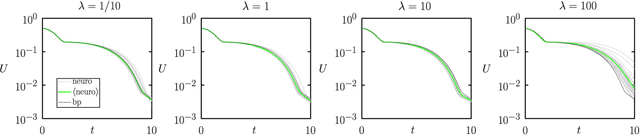
Correspondence between neuroevolution and gradient descent

We show analytically that training a neural network by stochastic mutation or "neuroevolution" of its weights is equivalent, in the limit of small mutations, to gradient descent on the loss function in the presence of Gaussian white noise. Averaged over independent realizations of the learning process, neuroevolution is equivalent to gradient descent on the loss function. We use numerical simulation to show that this correspondence can be observed for finite mutations. Our results provide a connection between two distinct types of neural-network training, and provide justification for the empirical success of neuroevolution.