Not All Language Model Features Are Linear

Recent work has proposed the linear representation hypothesis: that language models perform computation by manipulating one-dimensional representations of concepts ("features") in activation space. In contrast, we explore whether some language model representations may be inherently multi-dimensional. We begin by developing a rigorous definition of irreducible multi-dimensional features based on whether they can be decomposed into either independent or non-co-occurring lower-dimensional features. Motivated by these definitions, we design a scalable method that uses sparse autoencoders to automatically find multi-dimensional features in GPT-2 and Mistral 7B. These auto-discovered features include strikingly interpretable examples, e.g. circular features representing days of the week and months of the year. We identify tasks where these exact circles are used to solve computational problems involving modular arithmetic in days of the week and months of the year. Finally, we provide evidence that these circular features are indeed the fundamental unit of computation in these tasks with intervention experiments on Mistral 7B and Llama 3 8B, and we find further circular representations by breaking down the hidden states for these tasks into interpretable components.

Opening the AI black box: program synthesis via mechanistic interpretability

We present MIPS, a novel method for program synthesis based on automated mechanistic interpretability of neural networks trained to perform the desired task, auto-distilling the learned algorithm into Python code. We test MIPS on a benchmark of 62 algorithmic tasks that can be learned by an RNN and find it highly complementary to GPT-4: MIPS solves 32 of them, including 13 that are not solved by GPT-4 (which also solves 30). MIPS uses an integer autoencoder to convert the RNN into a finite state machine, then applies Boolean or integer symbolic regression to capture the learned algorithm. As opposed to large language models, this program synthesis technique makes no use of (and is therefore not limited by) human training data such as algorithms and code from GitHub. We discuss opportunities and challenges for scaling up this approach to make machine-learned models more interpretable and trustworthy.

Generating Interpretable Networks using Hypernetworks

An essential goal in mechanistic interpretability to decode a network, i.e., to convert a neural network's raw weights to an interpretable algorithm. Given the difficulty of the decoding problem, progress has been made to understand the easier encoding problem, i.e., to convert an interpretable algorithm into network weights. Previous works focus on encoding existing algorithms into networks, which are interpretable by definition. However, focusing on encoding limits the possibility of discovering new algorithms that humans have never stumbled upon, but that are nevertheless interpretable. In this work, we explore the possibility of using hypernetworks to generate interpretable networks whose underlying algorithms are not yet known. The hypernetwork is carefully designed such that it can control network complexity, leading to a diverse family of interpretable algorithms ranked by their complexity. All of them are interpretable in hindsight, although some of them are less intuitive to humans, hence providing new insights regarding how to "think" like a neural network. For the task of computing L1 norms, hypernetworks find three algorithms: (a) the double-sided algorithm, (b) the convexity algorithm, (c) the pudding algorithm, although only the first algorithm was expected by the authors before experiments. We automatically classify these algorithms and analyze how these algorithmic phases develop during training, as well as how they are affected by complexity control. Furthermore, we show that a trained hypernetwork can correctly construct models for input dimensions not seen in training, demonstrating systematic generalization.

Learning to Optimize Quasi-Newton Methods

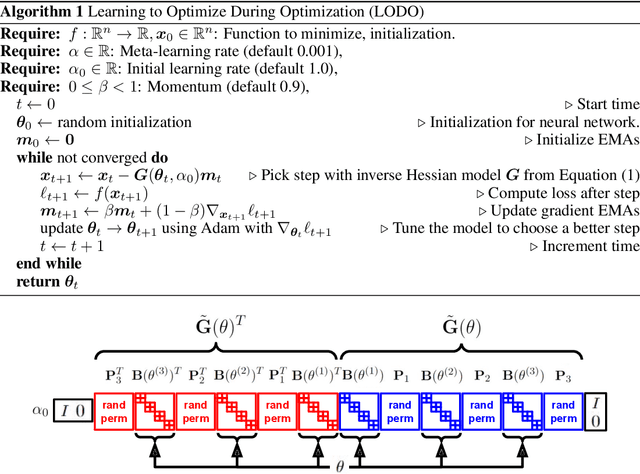
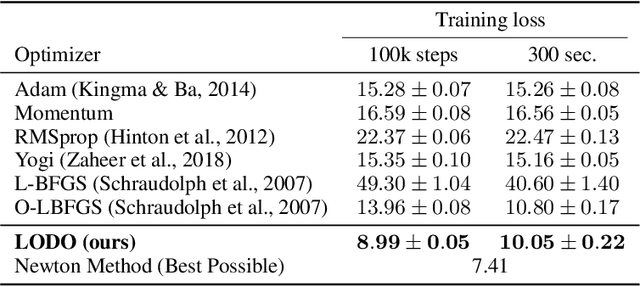
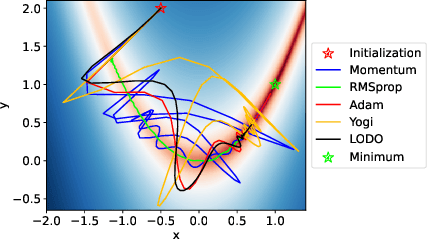
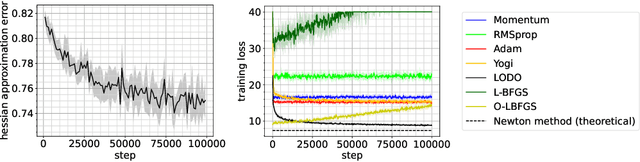
We introduce a novel machine learning optimizer called LODO, which online meta-learns an implicit inverse Hessian of the loss as a subroutine of quasi-Newton optimization. Our optimizer merges Learning to Optimize (L2O) techniques with quasi-Newton methods to learn neural representations of symmetric matrix vector products, which are more flexible than those in other quasi-Newton methods. Unlike other L2O methods, ours does not require any meta-training on a training task distribution, and instead learns to optimize on the fly while optimizing on the test task, adapting to the local characteristics of the loss landscape while traversing it. Theoretically, we show that our optimizer approximates the inverse Hessian in noisy loss landscapes and is capable of representing a wide range of inverse Hessians. We experimentally verify our algorithm's performance in the presence of noise, and show that simpler alternatives for representing the inverse Hessians worsen performance. Lastly, we use our optimizer to train a semi-realistic deep neural network with 95k parameters, and obtain competitive results against standard neural network optimizers.