A Rational Distributed Process-level Account of Independence Judgment

It is inconceivable how chaotic the world would look to humans, faced with innumerable decisions a day to be made under uncertainty, had they been lacking the capacity to distinguish the relevant from the irrelevant---a capacity which computationally amounts to handling probabilistic independence relations. The highly parallel and distributed computational machinery of the brain suggests that a satisfying process-level account of human independence judgment should also mimic these features. In this work, we present the first rational, distributed, message-passing, process-level account of independence judgment, called $\mathcal{D}^\ast$. Interestingly, $\mathcal{D}^\ast$ shows a curious, but normatively-justified tendency for quick detection of dependencies, whenever they hold. Furthermore, $\mathcal{D}^\ast$ outperforms all the previously proposed algorithms in the AI literature in terms of worst-case running time, and a salient aspect of it is supported by recent work in neuroscience investigating possible implementations of Bayes nets at the neural level. $\mathcal{D}^\ast$ nicely exemplifies how the pursuit of cognitive plausibility can lead to the discovery of state-of-the-art algorithms with appealing properties, and its simplicity makes $\mathcal{D}^\ast$ potentially a good candidate for pedagogical purposes.

The Causal Frame Problem: An Algorithmic Perspective

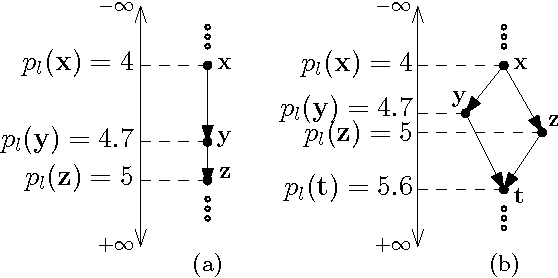
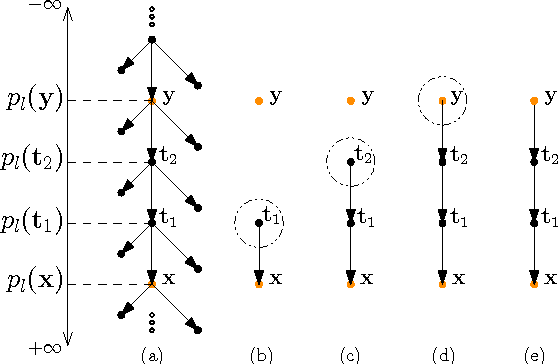
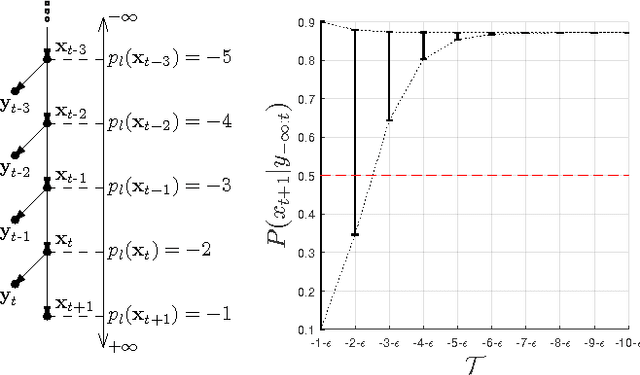
The Frame Problem (FP) is a puzzle in philosophy of mind and epistemology, articulated by the Stanford Encyclopedia of Philosophy as follows: "How do we account for our apparent ability to make decisions on the basis only of what is relevant to an ongoing situation without having explicitly to consider all that is not relevant?" In this work, we focus on the causal variant of the FP, the Causal Frame Problem (CFP). Assuming that a reasoner's mental causal model can be (implicitly) represented by a causal Bayes net, we first introduce a notion called Potential Level (PL). PL, in essence, encodes the relative position of a node with respect to its neighbors in a causal Bayes net. Drawing on the psychological literature on causal judgment, we substantiate the claim that PL may bear on how time is encoded in the mind. Using PL, we propose an inference framework, called the PL-based Inference Framework (PLIF), which permits a boundedly-rational approach to the CFP to be formally articulated at Marr's algorithmic level of analysis. We show that our proposed framework, PLIF, is consistent with a wide range of findings in causal judgment literature, and that PL and PLIF make a number of predictions, some of which are already supported by existing findings.

Probabilistic Structural Controllability in Causal Bayesian Networks

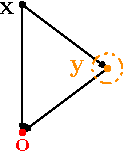
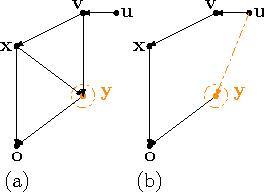
Humans routinely confront the following key question which could be viewed as a probabilistic variant of the controllability problem: While faced with an uncertain environment governed by causal structures, how should they practice their autonomy by intervening on driver variables, in order to increase (or decrease) the probability of attaining their desired (or undesired) state for some target variable? In this paper, for the first time, the problem of probabilistic controllability in Causal Bayesian Networks (CBNs) is studied. More specifically, the aim of this paper is two-fold: (i) to introduce and formalize the problem of probabilistic structural controllability in CBNs, and (ii) to identify a sufficient set of driver variables for the purpose of probabilistic structural controllability of a generic CBN. We also elaborate on the nature of minimality the identified set of driver variables satisfies. In this context, the term "structural" signifies the condition wherein solely the structure of the CBN is known.

Multi-Context Models for Reasoning under Partial Knowledge: Generative Process and Inference Grammar

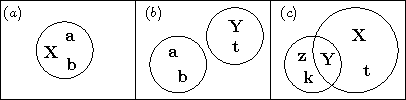
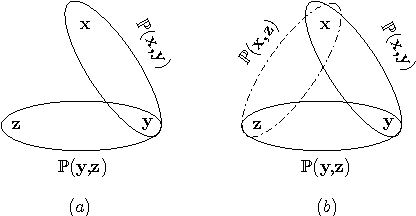
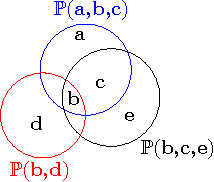
Arriving at the complete probabilistic knowledge of a domain, i.e., learning how all variables interact, is indeed a demanding task. In reality, settings often arise for which an individual merely possesses partial knowledge of the domain, and yet, is expected to give adequate answers to a variety of posed queries. That is, although precise answers to some queries, in principle, cannot be achieved, a range of plausible answers is attainable for each query given the available partial knowledge. In this paper, we propose the Multi-Context Model (MCM), a new graphical model to represent the state of partial knowledge as to a domain. MCM is a middle ground between Probabilistic Logic, Bayesian Logic, and Probabilistic Graphical Models. For this model we discuss: (i) the dynamics of constructing a contradiction-free MCM, i.e., to form partial beliefs regarding a domain in a gradual and probabilistically consistent way, and (ii) how to perform inference, i.e., to evaluate a probability of interest involving some variables of the domain.