Ilya Shpitser
On the definition of a confounder
Apr 02, 2013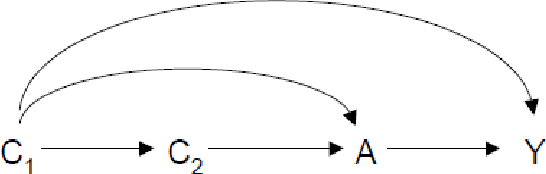
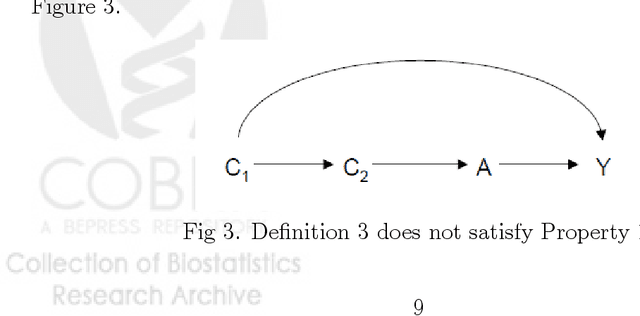
Abstract:The causal inference literature has provided a clear formal definition of confounding expressed in terms of counterfactual independence. The literature has not, however, come to any consensus on a formal definition of a confounder, as it has given priority to the concept of confounding over that of a confounder. We consider a number of candidate definitions arising from various more informal statements made in the literature. We consider the properties satisfied by each candidate definition, principally focusing on (i) whether under the candidate definition control for all "confounders" suffices to control for "confounding" and (ii) whether each confounder in some context helps eliminate or reduce confounding bias. Several of the candidate definitions do not have these two properties. Only one candidate definition of those considered satisfies both properties. We propose that a "confounder" be defined as a pre-exposure covariate C for which there exists a set of other covariates X such that effect of the exposure on the outcome is unconfounded conditional on (X,C) but such that for no proper subset of (X,C) is the effect of the exposure on the outcome unconfounded given the subset. We also provide a conditional analogue of the above definition; and we propose a variable that helps reduce bias but not eliminate bias be referred to as a "surrogate confounder." These definitions are closely related to those given by Robins and Morgenstern [Comput. Math. Appl. 14 (1987) 869-916]. The implications that hold among the various candidate definitions are discussed.
* Published in at http://dx.doi.org/10.1214/12-AOS1058 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Parameter and Structure Learning in Nested Markov Models
Jul 20, 2012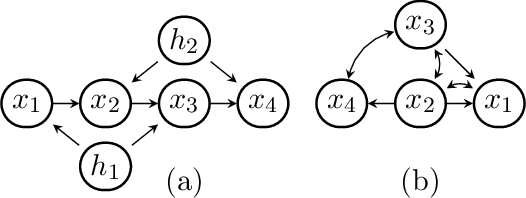
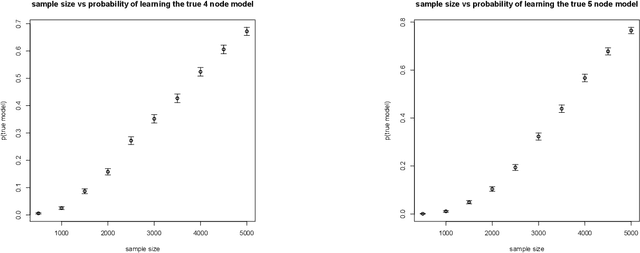
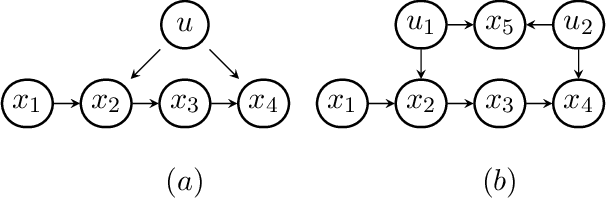
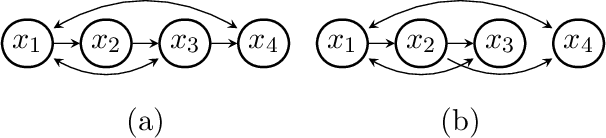
Abstract:The constraints arising from DAG models with latent variables can be naturally represented by means of acyclic directed mixed graphs (ADMGs). Such graphs contain directed and bidirected arrows, and contain no directed cycles. DAGs with latent variables imply independence constraints in the distribution resulting from a 'fixing' operation, in which a joint distribution is divided by a conditional. This operation generalizes marginalizing and conditioning. Some of these constraints correspond to identifiable 'dormant' independence constraints, with the well known 'Verma constraint' as one example. Recently, models defined by a set of the constraints arising after fixing from a DAG with latents, were characterized via a recursive factorization and a nested Markov property. In addition, a parameterization was given in the discrete case. In this paper we use this parameterization to describe a parameter fitting algorithm, and a search and score structure learning algorithm for these nested Markov models. We apply our algorithms to a variety of datasets.
Identification of Conditional Interventional Distributions
Jun 27, 2012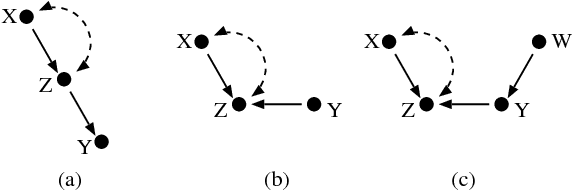
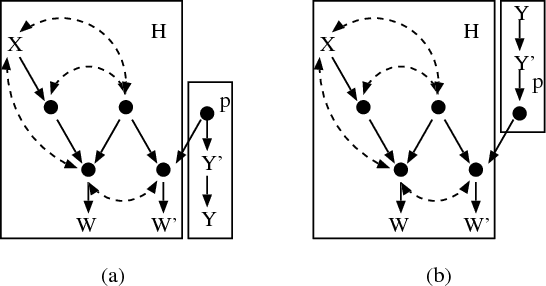
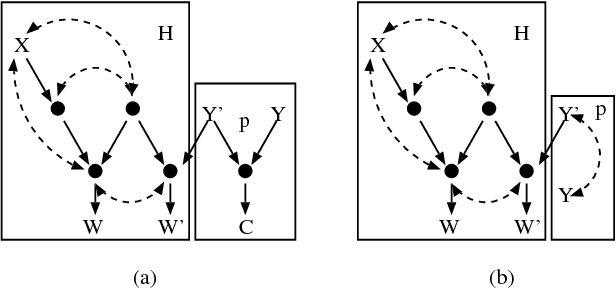
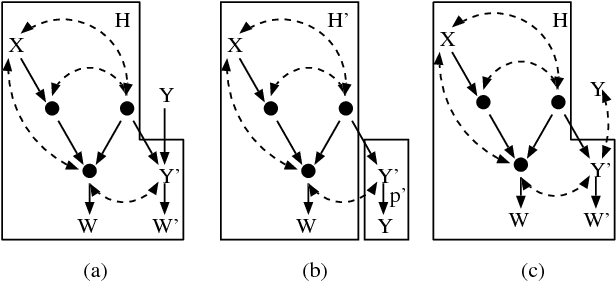
Abstract:The subject of this paper is the elucidation of effects of actions from causal assumptions represented as a directed graph, and statistical knowledge given as a probability distribution. In particular, we are interested in predicting conditional distributions resulting from performing an action on a set of variables and, subsequently, taking measurements of another set. We provide a necessary and sufficient graphical condition for the cases where such distributions can be uniquely computed from the available information, as well as an algorithm which performs this computation whenever the condition holds. Furthermore, we use our results to prove completeness of do-calculus [Pearl, 1995] for the same identification problem.
What Counterfactuals Can Be Tested
Jun 20, 2012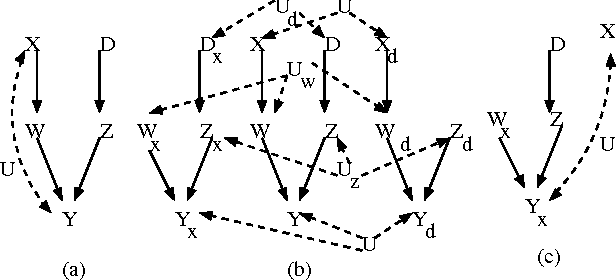
Abstract:Counterfactual statements, e.g., "my headache would be gone had I taken an aspirin" are central to scientific discourse, and are formally interpreted as statements derived from "alternative worlds". However, since they invoke hypothetical states of affairs, often incompatible with what is actually known or observed, testing counterfactuals is fraught with conceptual and practical difficulties. In this paper, we provide a complete characterization of "testable counterfactuals," namely, counterfactual statements whose probabilities can be inferred from physical experiments. We provide complete procedures for discerning whether a given counterfactual is testable and, if so, expressing its probability in terms of experimental data.
Effects of Treatment on the Treated: Identification and Generalization
May 09, 2012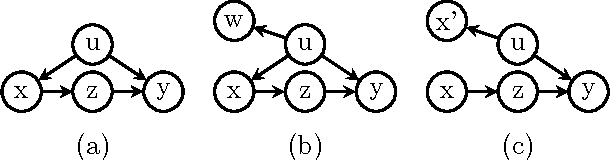
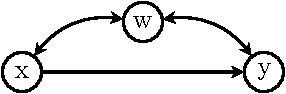
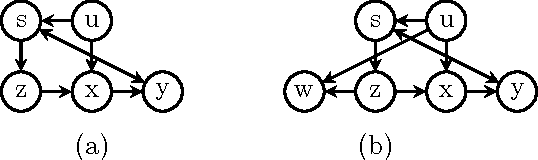
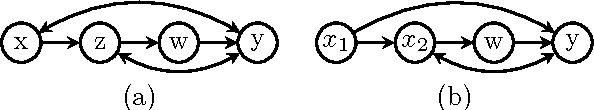
Abstract:Many applications of causal analysis call for assessing, retrospectively, the effect of withholding an action that has in fact been implemented. This counterfactual quantity, sometimes called "effect of treatment on the treated," (ETT) have been used to to evaluate educational programs, critic public policies, and justify individual decision making. In this paper we explore the conditions under which ETT can be estimated from (i.e., identified in) experimental and/or observational studies. We show that, when the action invokes a singleton variable, the conditions for ETT identification have simple characterizations in terms of causal diagrams. We further give a graphical characterization of the conditions under which the effects of multiple treatments on the treated can be identified, as well as ways in which the ETT estimand can be constructed from both interventional and observational distributions.
On the Validity of Covariate Adjustment for Estimating Causal Effects
Mar 15, 2012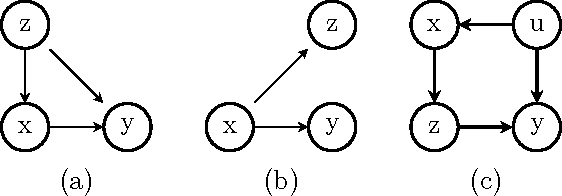
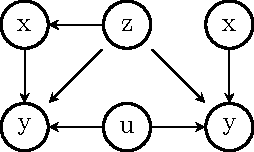
Abstract:Identifying effects of actions (treatments) on outcome variables from observational data and causal assumptions is a fundamental problem in causal inference. This identification is made difficult by the presence of confounders which can be related to both treatment and outcome variables. Confounders are often handled, both in theory and in practice, by adjusting for covariates, in other words considering outcomes conditioned on treatment and covariate values, weighed by probability of observing those covariate values. In this paper, we give a complete graphical criterion for covariate adjustment, which we term the adjustment criterion, and derive some interesting corollaries of the completeness of this criterion.
An Efficient Algorithm for Computing Interventional Distributions in Latent Variable Causal Models
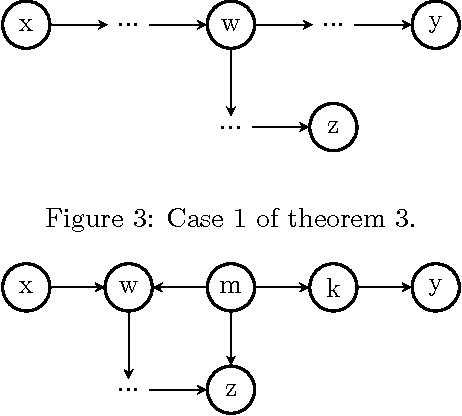
Feb 14, 2012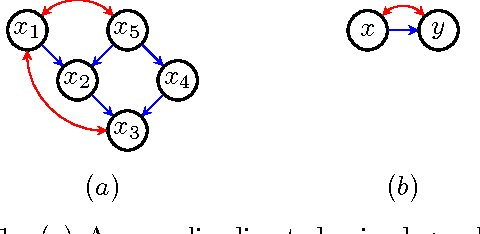
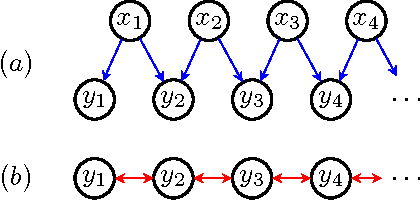
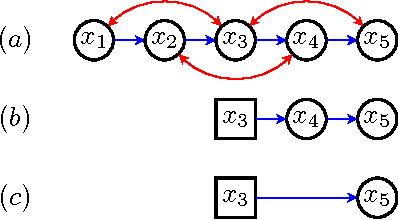
Abstract:Probabilistic inference in graphical models is the task of computing marginal and conditional densities of interest from a factorized representation of a joint probability distribution. Inference algorithms such as variable elimination and belief propagation take advantage of constraints embedded in this factorization to compute such densities efficiently. In this paper, we propose an algorithm which computes interventional distributions in latent variable causal models represented by acyclic directed mixed graphs(ADMGs). To compute these distributions efficiently, we take advantage of a recursive factorization which generalizes the usual Markov factorization for DAGs and the more recent factorization for ADMGs. Our algorithm can be viewed as a generalization of variable elimination to the mixed graph case. We show our algorithm is exponential in the mixed graph generalization of treewidth.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge