List-Decodable Mean Estimation in Nearly-PCA Time

Traditionally, robust statistics has focused on designing estimators tolerant to a minority of contaminated data. Robust list-decodable learning focuses on the more challenging regime where only a minority $\frac 1 k$ fraction of the dataset is drawn from the distribution of interest, and no assumptions are made on the remaining data. We study the fundamental task of list-decodable mean estimation in high dimensions. Our main result is a new list-decodable mean estimation algorithm for bounded covariance distributions with optimal sample complexity and error rate, running in nearly-PCA time. Assuming the ground truth distribution on $\mathbb{R}^d$ has bounded covariance, our algorithm outputs a list of $O(k)$ candidate means, one of which is within distance $O(\sqrt{k})$ from the truth. Our algorithm runs in time $\widetilde{O}(ndk)$ for all $k = O(\sqrt{d}) \cup \Omega(d)$, where $n$ is the size of the dataset. We also show that a variant of our algorithm has runtime $\widetilde{O}(ndk)$ for all $k$, at the expense of an $O(\sqrt{\log k})$ factor in the recovery guarantee. This runtime matches up to logarithmic factors the cost of performing a single $k$-PCA on the data, which is a natural bottleneck of known algorithms for (very) special cases of our problem, such as clustering well-separated mixtures. Prior to our work, the fastest list-decodable mean estimation algorithms had runtimes $\widetilde{O}(n^2 d k^2)$ and $\widetilde{O}(nd k^{\ge 6})$. Our approach builds on a novel soft downweighting method, $\mathsf{SIFT}$, which is arguably the simplest known polynomial-time mean estimation technique in the list-decodable learning setting. To develop our fast algorithms, we boost the computational cost of $\mathsf{SIFT}$ via a careful "win-win-win" analysis of an approximate Ky Fan matrix multiplicative weights procedure we develop, which we believe may be of independent interest.

A Polynomial Time Algorithm for Learning Halfspaces with Tsybakov Noise

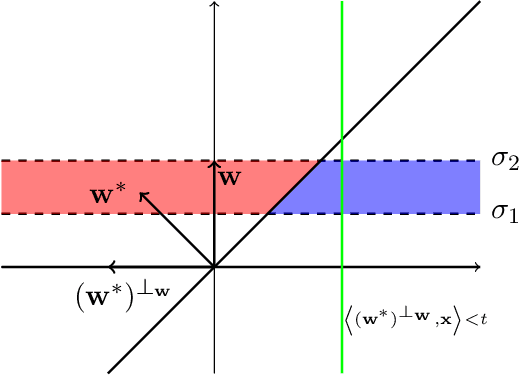
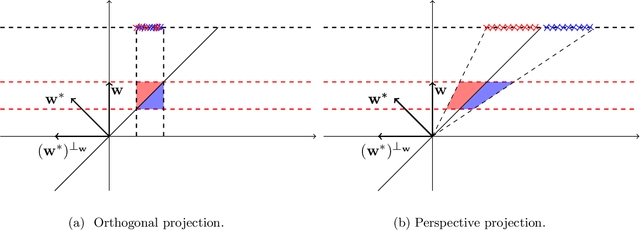
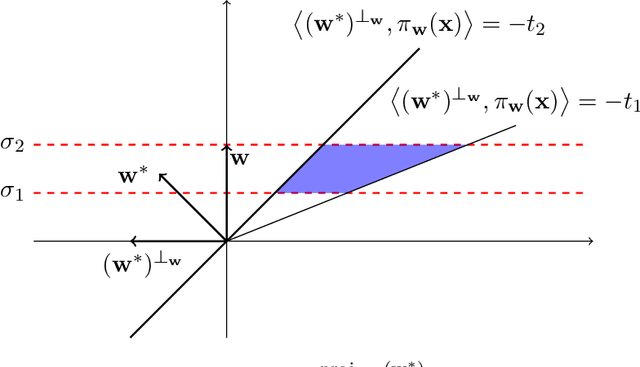
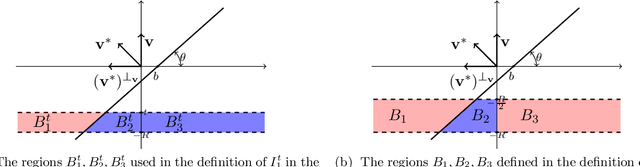
We study the problem of PAC learning homogeneous halfspaces in the presence of Tsybakov noise. In the Tsybakov noise model, the label of every sample is independently flipped with an adversarially controlled probability that can be arbitrarily close to $1/2$ for a fraction of the samples. {\em We give the first polynomial-time algorithm for this fundamental learning problem.} Our algorithm learns the true halfspace within any desired accuracy $\epsilon$ and succeeds under a broad family of well-behaved distributions including log-concave distributions. Prior to our work, the only previous algorithm for this problem required quasi-polynomial runtime in $1/\epsilon$. Our algorithm employs a recently developed reduction \cite{DKTZ20b} from learning to certifying the non-optimality of a candidate halfspace. This prior work developed a quasi-polynomial time certificate algorithm based on polynomial regression. {\em The main technical contribution of the current paper is the first polynomial-time certificate algorithm.} Starting from a non-trivial warm-start, our algorithm performs a novel "win-win" iterative process which, at each step, either finds a valid certificate or improves the angle between the current halfspace and the true one. Our warm-start algorithm for isotropic log-concave distributions involves a number of analytic tools that may be of broader interest. These include a new efficient method for reweighting the distribution in order to recenter it and a novel characterization of the spectrum of the degree-$2$ Chow parameters.

Optimal Testing of Discrete Distributions with High Probability

We study the problem of testing discrete distributions with a focus on the high probability regime. Specifically, given samples from one or more discrete distributions, a property $\mathcal{P}$, and parameters $0< \epsilon, \delta <1$, we want to distinguish {\em with probability at least $1-\delta$} whether these distributions satisfy $\mathcal{P}$ or are $\epsilon$-far from $\mathcal{P}$ in total variation distance. Most prior work in distribution testing studied the constant confidence case (corresponding to $\delta = \Omega(1)$), and provided sample-optimal testers for a range of properties. While one can always boost the confidence probability of any such tester by black-box amplification, this generic boosting method typically leads to sub-optimal sample bounds. Here we study the following broad question: For a given property $\mathcal{P}$, can we {\em characterize} the sample complexity of testing $\mathcal{P}$ as a function of all relevant problem parameters, including the error probability $\delta$? Prior to this work, uniformity testing was the only statistical task whose sample complexity had been characterized in this setting. As our main results, we provide the first algorithms for closeness and independence testing that are sample-optimal, within constant factors, as a function of all relevant parameters. We also show matching information-theoretic lower bounds on the sample complexity of these problems. Our techniques naturally extend to give optimal testers for related problems. To illustrate the generality of our methods, we give optimal algorithms for testing collections of distributions and testing closeness with unequal sized samples.

Outlier Robust Mean Estimation with Subgaussian Rates via Stability

We study the problem of outlier robust high-dimensional mean estimation under a finite covariance assumption, and more broadly under finite low-degree moment assumptions. We consider a standard stability condition from the recent robust statistics literature and prove that, except with exponentially small failure probability, there exists a large fraction of the inliers satisfying this condition. As a corollary, it follows that a number of recently developed algorithms for robust mean estimation, including iterative filtering and non-convex gradient descent, give optimal error estimators with (near-)subgaussian rates. Previous analyses of these algorithms gave significantly suboptimal rates. As a corollary of our approach, we obtain the first computationally efficient algorithm with subgaussian rate for outlier-robust mean estimation in the strong contamination model under a finite covariance assumption.

The Complexity of Adversarially Robust Proper Learning of Halfspaces with Agnostic Noise

We study the computational complexity of adversarially robust proper learning of halfspaces in the distribution-independent agnostic PAC model, with a focus on $L_p$ perturbations. We give a computationally efficient learning algorithm and a nearly matching computational hardness result for this problem. An interesting implication of our findings is that the $L_{\infty}$ perturbations case is provably computationally harder than the case $2 \leq p < \infty$.

Near-Optimal SQ Lower Bounds for Agnostically Learning Halfspaces and ReLUs under Gaussian Marginals

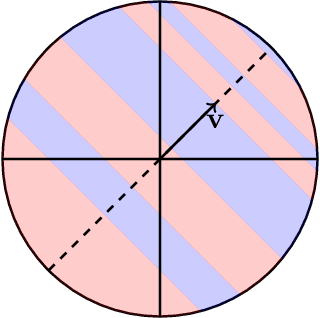
We study the fundamental problems of agnostically learning halfspaces and ReLUs under Gaussian marginals. In the former problem, given labeled examples $(\mathbf{x}, y)$ from an unknown distribution on $\mathbb{R}^d \times \{ \pm 1\}$, whose marginal distribution on $\mathbf{x}$ is the standard Gaussian and the labels $y$ can be arbitrary, the goal is to output a hypothesis with 0-1 loss $\mathrm{OPT}+\epsilon$, where $\mathrm{OPT}$ is the 0-1 loss of the best-fitting halfspace. In the latter problem, given labeled examples $(\mathbf{x}, y)$ from an unknown distribution on $\mathbb{R}^d \times \mathbb{R}$, whose marginal distribution on $\mathbf{x}$ is the standard Gaussian and the labels $y$ can be arbitrary, the goal is to output a hypothesis with square loss $\mathrm{OPT}+\epsilon$, where $\mathrm{OPT}$ is the square loss of the best-fitting ReLU. We prove Statistical Query (SQ) lower bounds of $d^{\mathrm{poly}(1/\epsilon)}$ for both of these problems. Our SQ lower bounds provide strong evidence that current upper bounds for these tasks are essentially best possible.

Algorithms and SQ Lower Bounds for PAC Learning One-Hidden-Layer ReLU Networks

We study the problem of PAC learning one-hidden-layer ReLU networks with $k$ hidden units on $\mathbb{R}^d$ under Gaussian marginals in the presence of additive label noise. For the case of positive coefficients, we give the first polynomial-time algorithm for this learning problem for $k$ up to $\tilde{O}(\sqrt{\log d})$. Previously, no polynomial time algorithm was known, even for $k=3$. This answers an open question posed by~\cite{Kliv17}. Importantly, our algorithm does not require any assumptions about the rank of the weight matrix and its complexity is independent of its condition number. On the negative side, for the more general task of PAC learning one-hidden-layer ReLU networks with arbitrary real coefficients, we prove a Statistical Query lower bound of $d^{\Omega(k)}$. Thus, we provide a separation between the two classes in terms of efficient learnability. Our upper and lower bounds are general, extending to broader families of activation functions.

List-Decodable Mean Estimation via Iterative Multi-Filtering

We study the problem of {\em list-decodable mean estimation} for bounded covariance distributions. Specifically, we are given a set $T$ of points in $\mathbb{R}^d$ with the promise that an unknown $\alpha$-fraction of points in $T$, where $0< \alpha < 1/2$, are drawn from an unknown mean and bounded covariance distribution $D$, and no assumptions are made on the remaining points. The goal is to output a small list of hypothesis vectors such that at least one of them is close to the mean of $D$. We give the first practically viable estimator for this problem. In more detail, our algorithm is sample and computationally efficient, and achieves information-theoretically near-optimal error. While the only prior algorithm for this setting inherently relied on the ellipsoid method, our algorithm is iterative and only uses spectral techniques. Our main technical innovation is the design of a soft outlier removal procedure for high-dimensional heavy-tailed datasets with a majority of outliers.

Non-Convex SGD Learns Halfspaces with Adversarial Label Noise

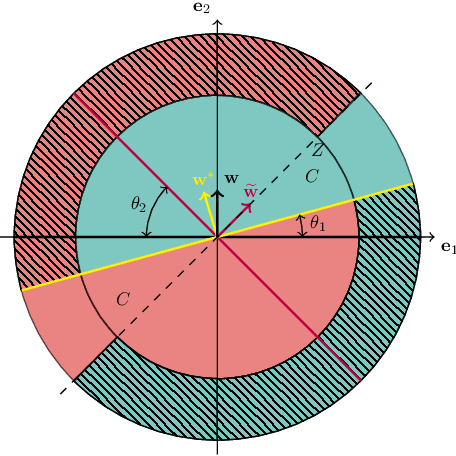
We study the problem of agnostically learning homogeneous halfspaces in the distribution-specific PAC model. For a broad family of structured distributions, including log-concave distributions, we show that non-convex SGD efficiently converges to a solution with misclassification error $O(\opt)+\eps$, where $\opt$ is the misclassification error of the best-fitting halfspace. In sharp contrast, we show that optimizing any convex surrogate inherently leads to misclassification error of $\omega(\opt)$, even under Gaussian marginals.

Learning Halfspaces with Tsybakov Noise

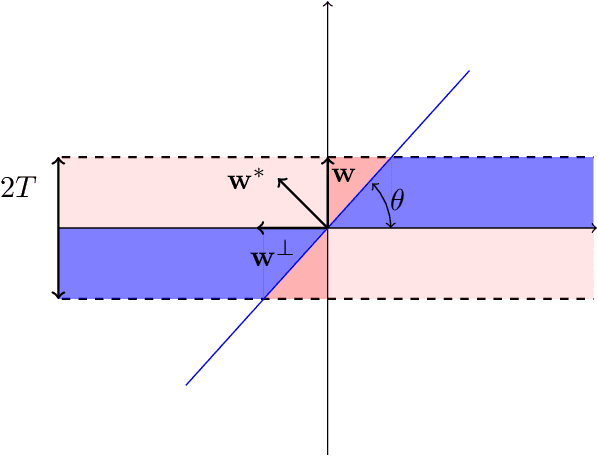
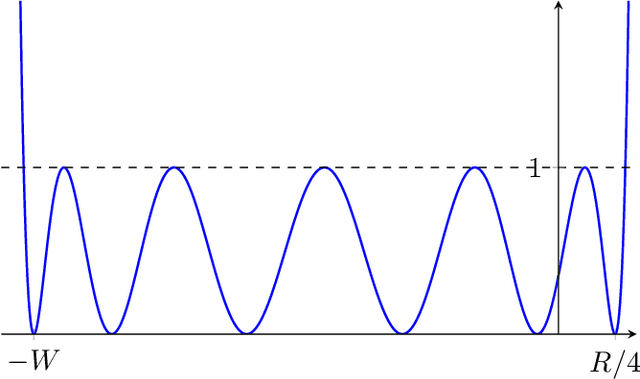
We study the efficient PAC learnability of halfspaces in the presence of Tsybakov noise. In the Tsybakov noise model, each label is independently flipped with some probability which is controlled by an adversary. This noise model significantly generalizes the Massart noise model, by allowing the flipping probabilities to be arbitrarily close to $1/2$ for a fraction of the samples. Our main result is the first non-trivial PAC learning algorithm for this problem under a broad family of structured distributions -- satisfying certain concentration and (anti-)anti-concentration properties -- including log-concave distributions. Specifically, we given an algorithm that achieves misclassification error $\epsilon$ with respect to the true halfspace, with quasi-polynomial runtime dependence in $1/\epsilin$. The only previous upper bound for this problem -- even for the special case of log-concave distributions -- was doubly exponential in $1/\epsilon$ (and follows via the naive reduction to agnostic learning). Our approach relies on a novel computationally efficient procedure to certify whether a candidate solution is near-optimal, based on semi-definite programming. We use this certificate procedure as a black-box and turn it into an efficient learning algorithm by searching over the space of halfspaces via online convex optimization.