Statistical Query Lower Bounds for List-Decodable Linear Regression

We study the problem of list-decodable linear regression, where an adversary can corrupt a majority of the examples. Specifically, we are given a set $T$ of labeled examples $(x, y) \in \mathbb{R}^d \times \mathbb{R}$ and a parameter $0< \alpha <1/2$ such that an $\alpha$-fraction of the points in $T$ are i.i.d. samples from a linear regression model with Gaussian covariates, and the remaining $(1-\alpha)$-fraction of the points are drawn from an arbitrary noise distribution. The goal is to output a small list of hypothesis vectors such that at least one of them is close to the target regression vector. Our main result is a Statistical Query (SQ) lower bound of $d^{\mathrm{poly}(1/\alpha)}$ for this problem. Our SQ lower bound qualitatively matches the performance of previously developed algorithms, providing evidence that current upper bounds for this task are nearly best possible.

Clustering Mixture Models in Almost-Linear Time via List-Decodable Mean Estimation

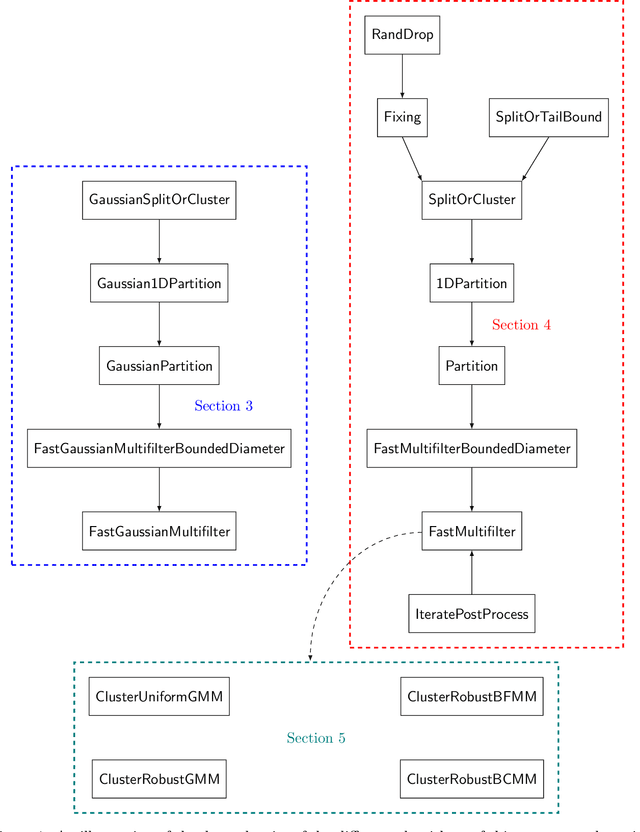
We study the problem of list-decodable mean estimation, where an adversary can corrupt a majority of the dataset. Specifically, we are given a set $T$ of $n$ points in $\mathbb{R}^d$ and a parameter $0< \alpha <\frac 1 2$ such that an $\alpha$-fraction of the points in $T$ are i.i.d. samples from a well-behaved distribution $\mathcal{D}$ and the remaining $(1-\alpha)$-fraction of the points are arbitrary. The goal is to output a small list of vectors at least one of which is close to the mean of $\mathcal{D}$. As our main contribution, we develop new algorithms for list-decodable mean estimation, achieving nearly-optimal statistical guarantees, with running time $n^{1 + o(1)} d$. All prior algorithms for this problem had additional polynomial factors in $\frac 1 \alpha$. As a corollary, we obtain the first almost-linear time algorithms for clustering mixtures of $k$ separated well-behaved distributions, nearly-matching the statistical guarantees of spectral methods. Prior clustering algorithms inherently relied on an application of $k$-PCA, thereby incurring runtimes of $\Omega(n d k)$. This marks the first runtime improvement for this basic statistical problem in nearly two decades. The starting point of our approach is a novel and simpler near-linear time robust mean estimation algorithm in the $\alpha \to 1$ regime, based on a one-shot matrix multiplicative weights-inspired potential decrease. We crucially leverage this new algorithmic framework in the context of the iterative multi-filtering technique of Diakonikolas et. al. '18, '20, providing a method to simultaneously cluster and downsample points using one-dimensional projections -- thus, bypassing the $k$-PCA subroutines required by prior algorithms.

Boosting in the Presence of Massart Noise

We study the problem of boosting the accuracy of a weak learner in the (distribution-independent) PAC model with Massart noise. In the Massart noise model, the label of each example $x$ is independently misclassified with probability $\eta(x) \leq \eta$, where $\eta<1/2$. The Massart model lies between the random classification noise model and the agnostic model. Our main positive result is the first computationally efficient boosting algorithm in the presence of Massart noise that achieves misclassification error arbitrarily close to $\eta$. Prior to our work, no non-trivial booster was known in this setting. Moreover, we show that this error upper bound is best possible for polynomial-time black-box boosters, under standard cryptographic assumptions. Our upper and lower bounds characterize the complexity of boosting in the distribution-independent PAC model with Massart noise. As a simple application of our positive result, we give the first efficient Massart learner for unions of high-dimensional rectangles.

Agnostic Proper Learning of Halfspaces under Gaussian Marginals

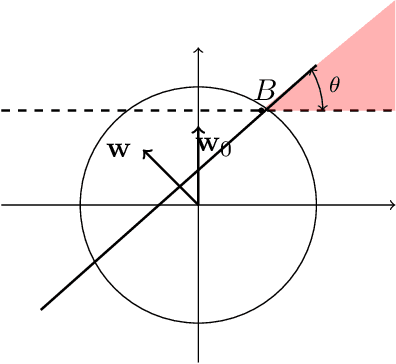
We study the problem of agnostically learning halfspaces under the Gaussian distribution. Our main result is the {\em first proper} learning algorithm for this problem whose sample complexity and computational complexity qualitatively match those of the best known improper agnostic learner. Building on this result, we also obtain the first proper polynomial-time approximation scheme (PTAS) for agnostically learning homogeneous halfspaces. Our techniques naturally extend to agnostically learning linear models with respect to other non-linear activations, yielding in particular the first proper agnostic algorithm for ReLU regression.

The Optimality of Polynomial Regression for Agnostic Learning under Gaussian Marginals

We study the problem of agnostic learning under the Gaussian distribution. We develop a method for finding hard families of examples for a wide class of problems by using LP duality. For Boolean-valued concept classes, we show that the $L^1$-regression algorithm is essentially best possible, and therefore that the computational difficulty of agnostically learning a concept class is closely related to the polynomial degree required to approximate any function from the class in $L^1$-norm. Using this characterization along with additional analytic tools, we obtain optimal SQ lower bounds for agnostically learning linear threshold functions and the first non-trivial SQ lower bounds for polynomial threshold functions and intersections of halfspaces. We also develop an analogous theory for agnostically learning real-valued functions, and as an application prove near-optimal SQ lower bounds for agnostically learning ReLUs and sigmoids.

Outlier-Robust Learning of Ising Models Under Dobrushin's Condition

We study the problem of learning Ising models satisfying Dobrushin's condition in the outlier-robust setting where a constant fraction of the samples are adversarially corrupted. Our main result is to provide the first computationally efficient robust learning algorithm for this problem with near-optimal error guarantees. Our algorithm can be seen as a special case of an algorithm for robustly learning a distribution from a general exponential family. To prove its correctness for Ising models, we establish new anti-concentration results for degree-$2$ polynomials of Ising models that may be of independent interest.

The Sample Complexity of Robust Covariance Testing

We study the problem of testing the covariance matrix of a high-dimensional Gaussian in a robust setting, where the input distribution has been corrupted in Huber's contamination model. Specifically, we are given i.i.d. samples from a distribution of the form $Z = (1-\epsilon) X + \epsilon B$, where $X$ is a zero-mean and unknown covariance Gaussian $\mathcal{N}(0, \Sigma)$, $B$ is a fixed but unknown noise distribution, and $\epsilon>0$ is an arbitrarily small constant representing the proportion of contamination. We want to distinguish between the cases that $\Sigma$ is the identity matrix versus $\gamma$-far from the identity in Frobenius norm. In the absence of contamination, prior work gave a simple tester for this hypothesis testing task that uses $O(d)$ samples. Moreover, this sample upper bound was shown to be best possible, within constant factors. Our main result is that the sample complexity of covariance testing dramatically increases in the contaminated setting. In particular, we prove a sample complexity lower bound of $\Omega(d^2)$ for $\epsilon$ an arbitrarily small constant and $\gamma = 1/2$. This lower bound is best possible, as $O(d^2)$ samples suffice to even robustly {\em learn} the covariance. The conceptual implication of our result is that, for the natural setting we consider, robust hypothesis testing is at least as hard as robust estimation.

Robustly Learning Mixtures of $k$ Arbitrary Gaussians

We give a polynomial-time algorithm for the problem of robustly estimating a mixture of $k$ arbitrary Gaussians in $\mathbb{R}^d$, for any fixed $k$, in the presence of a constant fraction of arbitrary corruptions. This resolves the main open problem in several previous works on algorithmic robust statistics, which addressed the special cases of robustly estimating (a) a single Gaussian, (b) a mixture of TV-distance separated Gaussians, and (c) a uniform mixture of two Gaussians. Our main tools are an efficient \emph{partial clustering} algorithm that relies on the sum-of-squares method, and a novel tensor decomposition algorithm that allows errors in both Frobenius norm and low-rank terms.

Hardness of Learning Halfspaces with Massart Noise

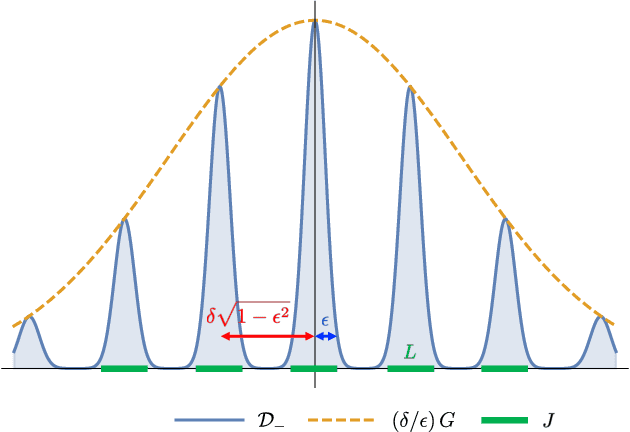
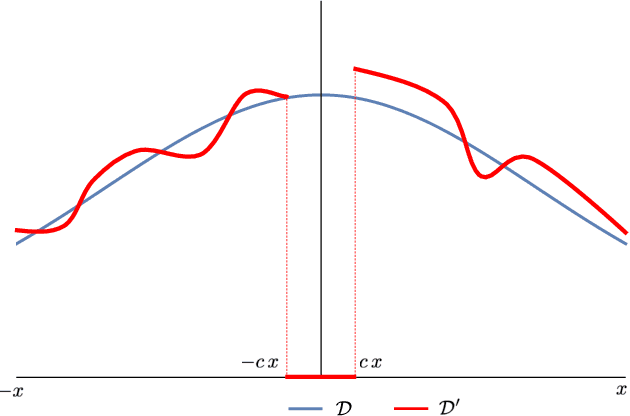
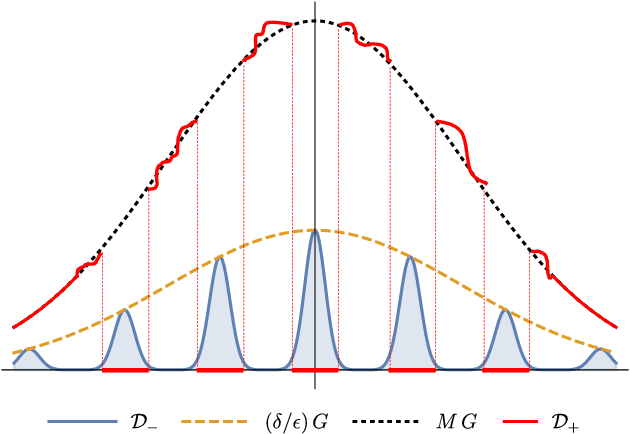
We study the complexity of PAC learning halfspaces in the presence of Massart (bounded) noise. Specifically, given labeled examples $(x, y)$ from a distribution $D$ on $\mathbb{R}^{n} \times \{ \pm 1\}$ such that the marginal distribution on $x$ is arbitrary and the labels are generated by an unknown halfspace corrupted with Massart noise at rate $\eta<1/2$, we want to compute a hypothesis with small misclassification error. Characterizing the efficient learnability of halfspaces in the Massart model has remained a longstanding open problem in learning theory. Recent work gave a polynomial-time learning algorithm for this problem with error $\eta+\epsilon$. This error upper bound can be far from the information-theoretically optimal bound of $\mathrm{OPT}+\epsilon$. More recent work showed that {\em exact learning}, i.e., achieving error $\mathrm{OPT}+\epsilon$, is hard in the Statistical Query (SQ) model. In this work, we show that there is an exponential gap between the information-theoretically optimal error and the best error that can be achieved by a polynomial-time SQ algorithm. In particular, our lower bound implies that no efficient SQ algorithm can approximate the optimal error within any polynomial factor.

Small Covers for Near-Zero Sets of Polynomials and Learning Latent Variable Models

Let $V$ be any vector space of multivariate degree-$d$ homogeneous polynomials with co-dimension at most $k$, and $S$ be the set of points where all polynomials in $V$ {\em nearly} vanish. We establish a qualitatively optimal upper bound on the size of $\epsilon$-covers for $S$, in the $\ell_2$-norm. Roughly speaking, we show that there exists an $\epsilon$-cover for $S$ of cardinality $M = (k/\epsilon)^{O_d(k^{1/d})}$. Our result is constructive yielding an algorithm to compute such an $\epsilon$-cover that runs in time $\mathrm{poly}(M)$. Building on our structural result, we obtain significantly improved learning algorithms for several fundamental high-dimensional probabilistic models with hidden variables. These include density and parameter estimation for $k$-mixtures of spherical Gaussians (with known common covariance), PAC learning one-hidden-layer ReLU networks with $k$ hidden units (under the Gaussian distribution), density and parameter estimation for $k$-mixtures of linear regressions (with Gaussian covariates), and parameter estimation for $k$-mixtures of hyperplanes. Our algorithms run in time {\em quasi-polynomial} in the parameter $k$. Previous algorithms for these problems had running times exponential in $k^{\Omega(1)}$. At a high-level our algorithms for all these learning problems work as follows: By computing the low-degree moments of the hidden parameters, we are able to find a vector space of polynomials that nearly vanish on the unknown parameters. Our structural result allows us to compute a quasi-polynomial sized cover for the set of hidden parameters, which we exploit in our learning algorithms.