CAISSON: Concept-Augmented Inference Suite of Self-Organizing Neural Networks

We present CAISSON, a novel hierarchical approach to Retrieval-Augmented Generation (RAG) that transforms traditional single-vector search into a multi-view clustering framework. At its core, CAISSON leverages dual Self-Organizing Maps (SOMs) to create complementary organizational views of the document space, where each view captures different aspects of document relationships through specialized embeddings. The first view processes combined text and metadata embeddings, while the second operates on metadata enriched with concept embeddings, enabling a comprehensive multi-view analysis that captures both fine-grained semantic relationships and high-level conceptual patterns. This dual-view approach enables more nuanced document discovery by combining evidence from different organizational perspectives. To evaluate CAISSON, we develop SynFAQA, a framework for generating synthetic financial analyst notes and question-answer pairs that systematically tests different aspects of information retrieval capabilities. Drawing on HotPotQA's methodology for constructing multi-step reasoning questions, SynFAQA generates controlled test cases where each question is paired with the set of notes containing its ground-truth answer, progressing from simple single-entity queries to complex multi-hop retrieval tasks involving multiple entities and concepts. Our experimental results demonstrate substantial improvements over both basic and enhanced RAG implementations, particularly for complex multi-entity queries, while maintaining practical response times suitable for interactive applications.

Model-Free Market Risk Hedging Using Crowding Networks

Crowding is widely regarded as one of the most important risk factors in designing portfolio strategies. In this paper, we analyze stock crowding using network analysis of fund holdings, which is used to compute crowding scores for stocks. These scores are used to construct costless long-short portfolios, computed in a distribution-free (model-free) way and without using any numerical optimization, with desirable properties of hedge portfolios. More specifically, these long-short portfolios provide protection for both small and large market price fluctuations, due to their negative correlation with the market and positive convexity as a function of market returns. By adding our long-short portfolio to a baseline portfolio such as a traditional 60/40 portfolio, our method provides an alternative way to hedge portfolio risk including tail risk, which does not require costly option-based strategies or complex numerical optimization. The total cost of such hedging amounts to the total cost of rebalancing the hedge portfolio.

Combining Reinforcement Learning and Inverse Reinforcement Learning for Asset Allocation Recommendations

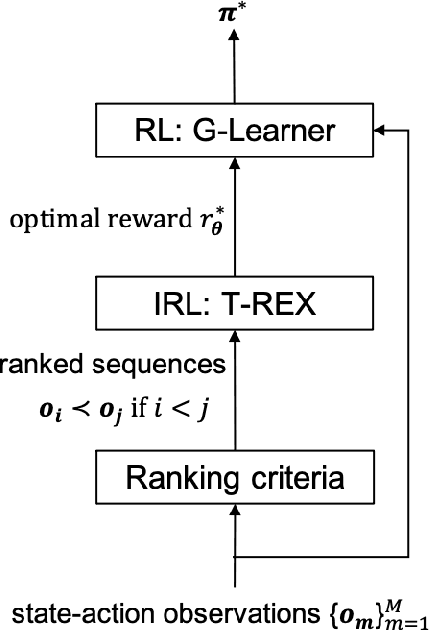
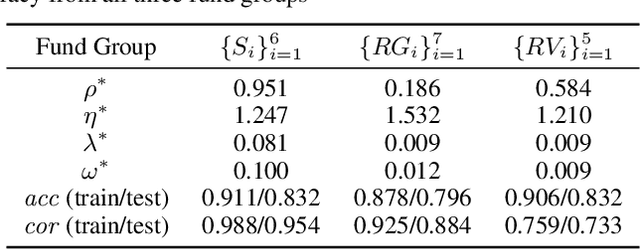
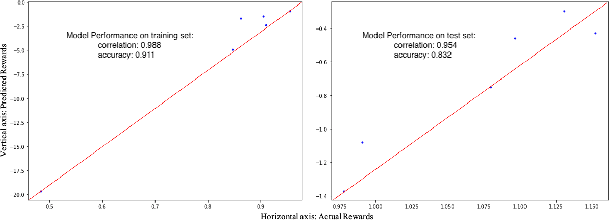
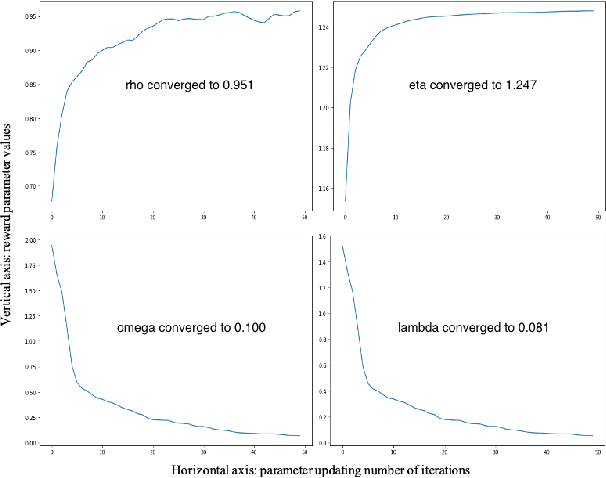
We suggest a simple practical method to combine the human and artificial intelligence to both learn best investment practices of fund managers, and provide recommendations to improve them. Our approach is based on a combination of Inverse Reinforcement Learning (IRL) and RL. First, the IRL component learns the intent of fund managers as suggested by their trading history, and recovers their implied reward function. At the second step, this reward function is used by a direct RL algorithm to optimize asset allocation decisions. We show that our method is able to improve over the performance of individual fund managers.

Distributional Offline Continuous-Time Reinforcement Learning with Neural Physics-Informed PDEs (SciPhy RL for DOCTR-L)

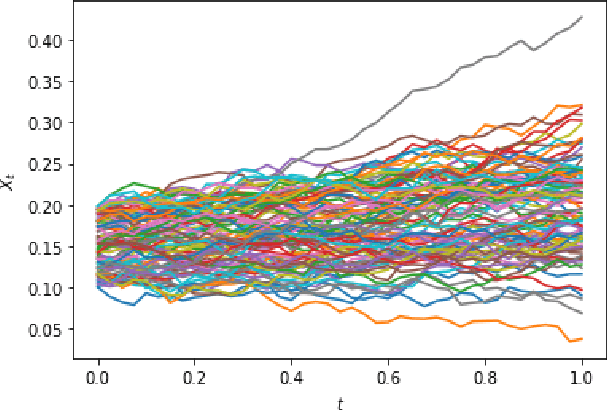
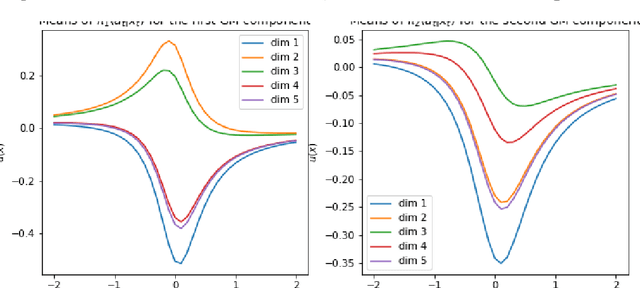
This paper addresses distributional offline continuous-time reinforcement learning (DOCTR-L) with stochastic policies for high-dimensional optimal control. A soft distributional version of the classical Hamilton-Jacobi-Bellman (HJB) equation is given by a semilinear partial differential equation (PDE). This `soft HJB equation' can be learned from offline data without assuming that the latter correspond to a previous optimal or near-optimal policy. A data-driven solution of the soft HJB equation uses methods of Neural PDEs and Physics-Informed Neural Networks developed in the field of Scientific Machine Learning (SciML). The suggested approach, dubbed `SciPhy RL', thus reduces DOCTR-L to solving neural PDEs from data. Our algorithm called Deep DOCTR-L converts offline high-dimensional data into an optimal policy in one step by reducing it to supervised learning, instead of relying on value iteration or policy iteration methods. The method enables a computable approach to the quality control of obtained policies in terms of both their expected returns and uncertainties about their values.

Non-Equilibrium Skewness, Market Crises, and Option Pricing: Non-Linear Langevin Model of Markets with Supersymmetry

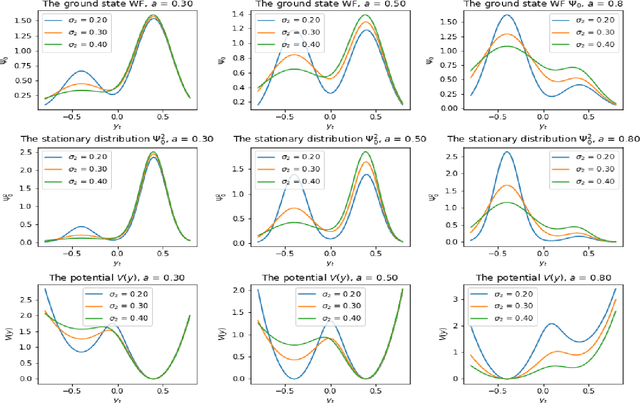
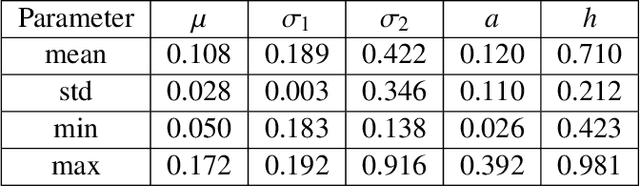
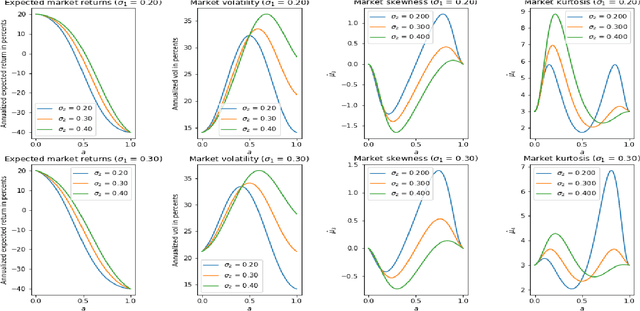
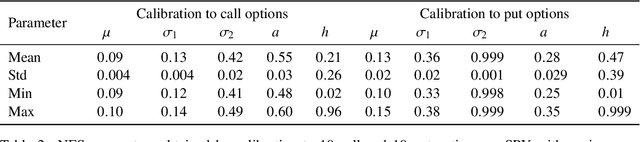
This paper presents a tractable model of non-linear dynamics of market returns using a Langevin approach.Due to non-linearity of an interaction potential, the model admits regimes of both small and large return fluctuations. Langevin dynamics are mapped onto an equivalent quantum mechanical (QM) system. Borrowing ideas from supersymmetric quantum mechanics (SUSY QM), we use a parameterized ground state wave function (WF) of this QM system as a direct input to the model, which also fixes a non-linear Langevin potential. A stationary distribution of the original Langevin model is given by the square of this WF, and thus is also a direct input to the model. Using a two-component Gaussian mixture as a ground state WF with an asymmetric double well potential produces a tractable low-parametric model with interpretable parameters, referred to as the NES (Non-Equilibrium Skew) model. Supersymmetry (SUSY) is then used to find time-dependent solutions of the model in an analytically tractable way. The model produces time-varying variance, skewness and kurtosis of market returns, whose time variability can be linked to probabilities of crisis-like events. For option pricing out of equilibrium, the NES model offers a closed-form approximation by a mixture of three Black-Scholes prices, which can be calibrated to index options data and used to predict moments of future returns. The NES model is shown to be able to describe both regimes of a benign market and a market in a crisis or a severe distress.

G-Learner and GIRL: Goal Based Wealth Management with Reinforcement Learning

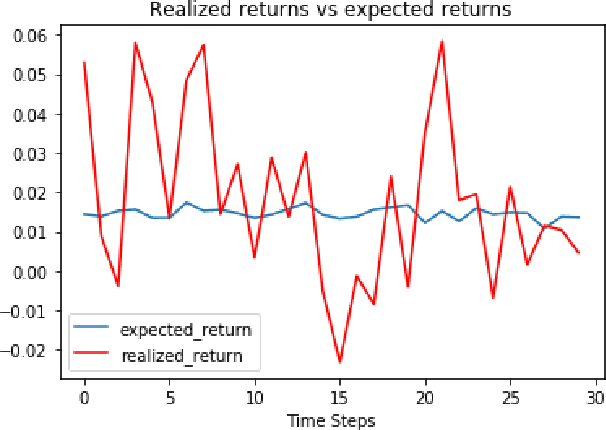
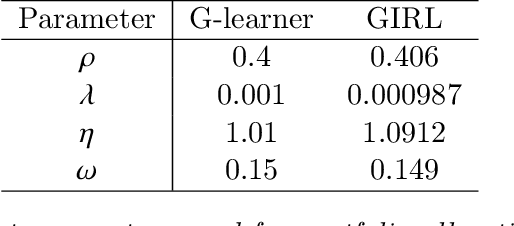
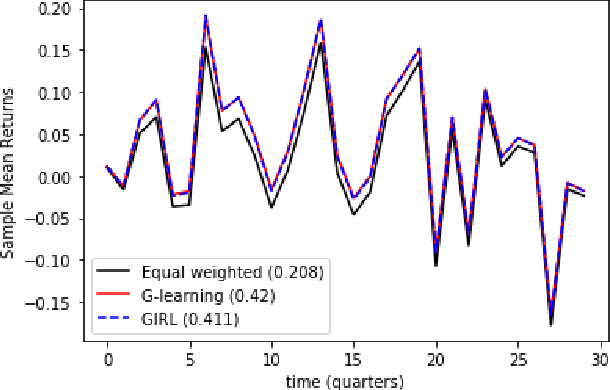
We present a reinforcement learning approach to goal based wealth management problems such as optimization of retirement plans or target dated funds. In such problems, an investor seeks to achieve a financial goal by making periodic investments in the portfolio while being employed, and periodically draws from the account when in retirement, in addition to the ability to re-balance the portfolio by selling and buying different assets (e.g. stocks). Instead of relying on a utility of consumption, we present G-Learner: a reinforcement learning algorithm that operates with explicitly defined one-step rewards, does not assume a data generation process, and is suitable for noisy data. Our approach is based on G-learning - a probabilistic extension of the Q-learning method of reinforcement learning. In this paper, we demonstrate how G-learning, when applied to a quadratic reward and Gaussian reference policy, gives an entropy-regulated Linear Quadratic Regulator (LQR). This critical insight provides a novel and computationally tractable tool for wealth management tasks which scales to high dimensional portfolios. In addition to the solution of the direct problem of G-learning, we also present a new algorithm, GIRL, that extends our goal-based G-learning approach to the setting of Inverse Reinforcement Learning (IRL) where rewards collected by the agent are not observed, and should instead be inferred. We demonstrate that GIRL can successfully learn the reward parameters of a G-Learner agent and thus imitate its behavior. Finally, we discuss potential applications of the G-Learner and GIRL algorithms for wealth management and robo-advising.

Market Self-Learning of Signals, Impact and Optimal Trading: Invisible Hand Inference with Free Energy

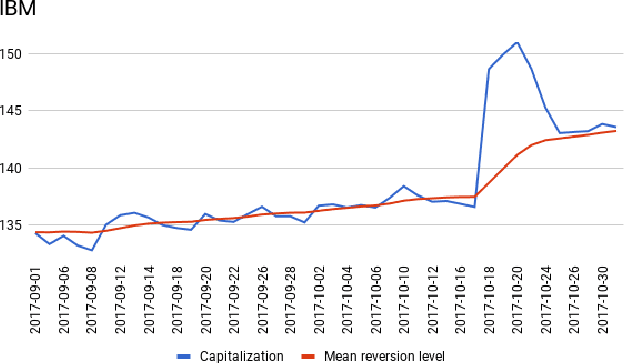
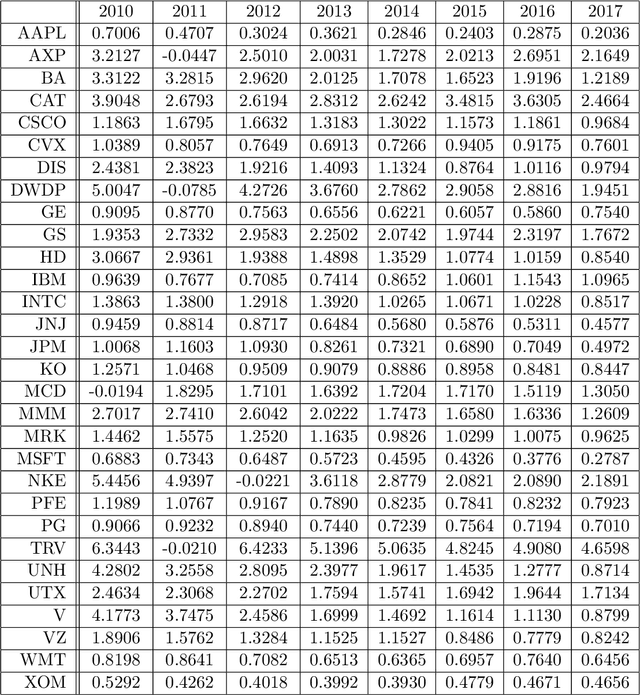
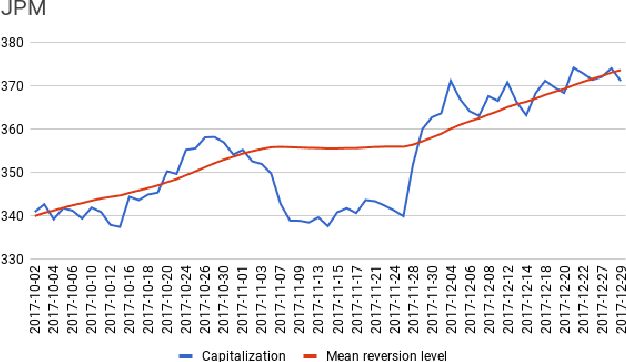
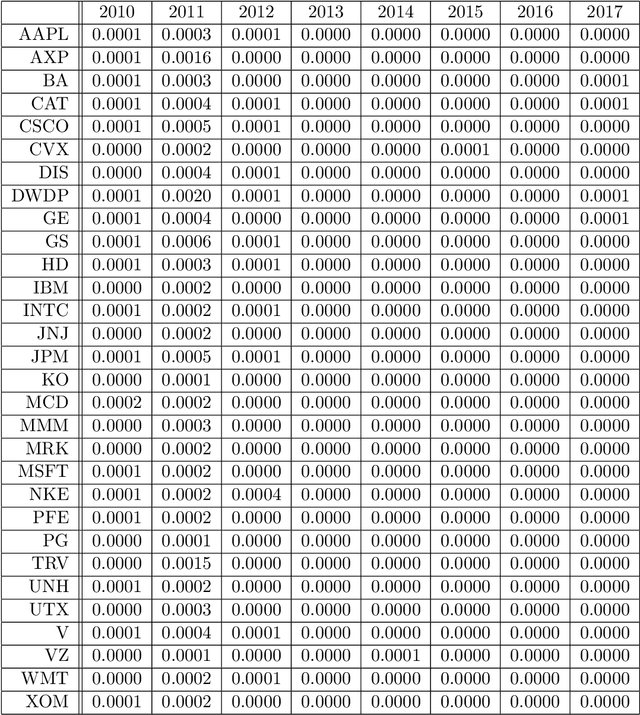
We present a simple model of a non-equilibrium self-organizing market where asset prices are partially driven by investment decisions of a bounded-rational agent. The agent acts in a stochastic market environment driven by various exogenous "alpha" signals, agent's own actions (via market impact), and noise. Unlike traditional agent-based models, our agent aggregates all traders in the market, rather than being a representative agent. Therefore, it can be identified with a bounded-rational component of the market itself, providing a particular implementation of an Invisible Hand market mechanism. In such setting, market dynamics are modeled as a fictitious self-play of such bounded-rational market-agent in its adversarial stochastic environment. As rewards obtained by such self-playing market agent are not observed from market data, we formulate and solve a simple model of such market dynamics based on a neuroscience-inspired Bounded Rational Information Theoretic Inverse Reinforcement Learning (BRIT-IRL). This results in effective asset price dynamics with a non-linear mean reversion - which in our model is generated dynamically, rather than being postulated. We argue that our model can be used in a similar way to the Black-Litterman model. In particular, it represents, in a simple modeling framework, market views of common predictive signals, market impacts and implied optimal dynamic portfolio allocations, and can be used to assess values of private signals. Moreover, it allows one to quantify a "market-implied" optimal investment strategy, along with a measure of market rationality. Our approach is numerically light, and can be implemented using standard off-the-shelf software such as TensorFlow.

The QLBS Q-Learner Goes NuQLear: Fitted Q Iteration, Inverse RL, and Option Portfolios

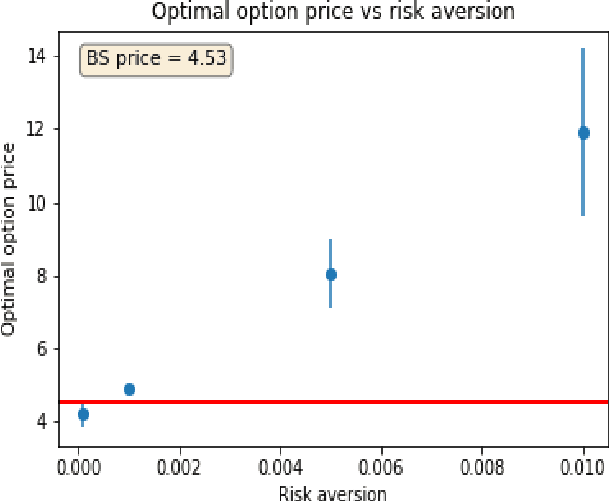
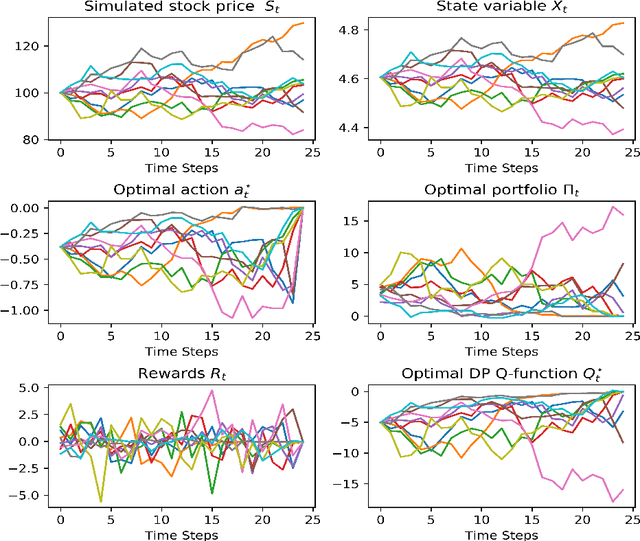
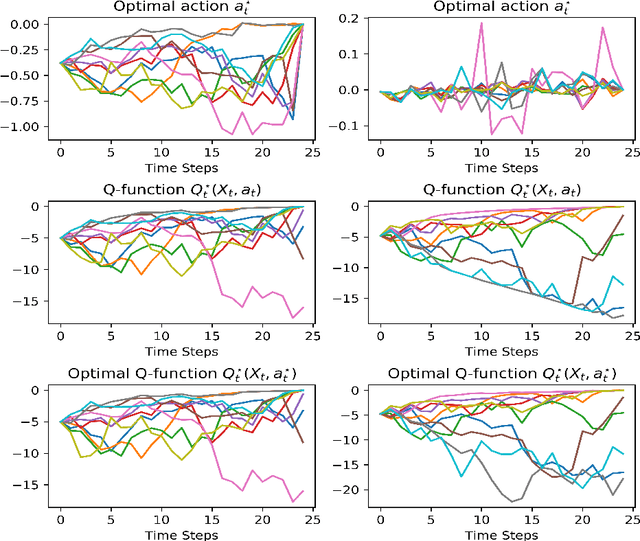
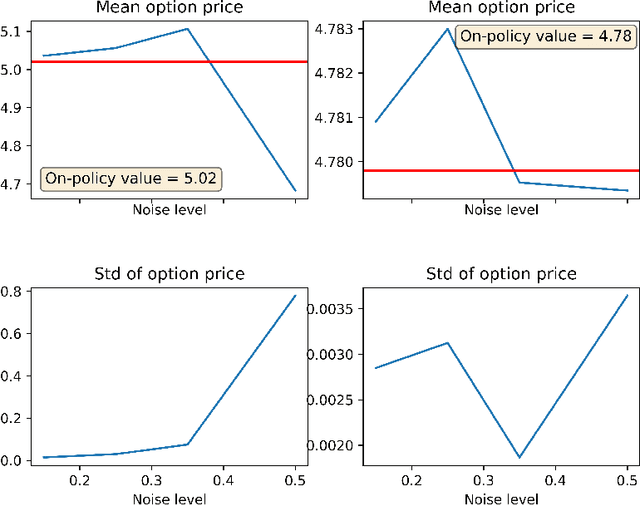
The QLBS model is a discrete-time option hedging and pricing model that is based on Dynamic Programming (DP) and Reinforcement Learning (RL). It combines the famous Q-Learning method for RL with the Black-Scholes (-Merton) model's idea of reducing the problem of option pricing and hedging to the problem of optimal rebalancing of a dynamic replicating portfolio for the option, which is made of a stock and cash. Here we expand on several NuQLear (Numerical Q-Learning) topics with the QLBS model. First, we investigate the performance of Fitted Q Iteration for a RL (data-driven) solution to the model, and benchmark it versus a DP (model-based) solution, as well as versus the BSM model. Second, we develop an Inverse Reinforcement Learning (IRL) setting for the model, where we only observe prices and actions (re-hedges) taken by a trader, but not rewards. Third, we outline how the QLBS model can be used for pricing portfolios of options, rather than a single option in isolation, thus providing its own, data-driven and model independent solution to the (in)famous volatility smile problem of the Black-Scholes model.

QLBS: Q-Learner in the Black-Scholes Worlds

This paper presents a discrete-time option pricing model that is rooted in Reinforcement Learning (RL), and more specifically in the famous Q-Learning method of RL. We construct a risk-adjusted Markov Decision Process for a discrete-time version of the classical Black-Scholes-Merton (BSM) model, where the option price is an optimal Q-function. Pricing is done by learning to dynamically optimize risk-adjusted returns for an option replicating portfolio, as in the Markowitz portfolio theory. Using Q-Learning and related methods, once created in a parametric setting, the model is able to go model-free and learn to price and hedge an option directly from data generated from a dynamic replicating portfolio which is rebalanced at discrete times. If the world is according to BSM, our risk-averse Q-Learner converges, given enough training data, to the true BSM price and hedge ratio of the option in the continuous time limit, even if hedges applied at the stage of data generation are completely random (i.e. it can learn the BSM model itself, too!), because Q-Learning is an off-policy algorithm. If the world is different from a BSM world, the Q-Learner will find it out as well, because Q-Learning is a model-free algorithm. For finite time steps, the Q-Learner is able to efficiently calculate both the optimal hedge and optimal price for the option directly from trading data, and without an explicit model of the world. This suggests that RL may provide efficient data-driven and model-free methods for optimal pricing and hedging of options, once we depart from the academic continuous-time limit, and vice versa, option pricing methods developed in Mathematical Finance may be viewed as special cases of model-based Reinforcement Learning. Our model only needs basic linear algebra (plus Monte Carlo simulation, if we work with synthetic data).

Inverse Reinforcement Learning for Marketing

Learning customer preferences from an observed behaviour is an important topic in the marketing literature. Structural models typically model forward-looking customers or firms as utility-maximizing agents whose utility is estimated using methods of Stochastic Optimal Control. We suggest an alternative approach to study dynamic consumer demand, based on Inverse Reinforcement Learning (IRL). We develop a version of the Maximum Entropy IRL that leads to a highly tractable model formulation that amounts to low-dimensional convex optimization in the search for optimal model parameters. Using simulations of consumer demand, we show that observational noise for identical customers can be easily confused with an apparent consumer heterogeneity.