Private Vector Mean Estimation in the Shuffle Model: Optimal Rates Require Many Messages

We study the problem of private vector mean estimation in the shuffle model of privacy where $n$ users each have a unit vector $v^{(i)} \in\mathbb{R}^d$. We propose a new multi-message protocol that achieves the optimal error using $\tilde{\mathcal{O}}\left(\min(n\varepsilon^2,d)\right)$ messages per user. Moreover, we show that any (unbiased) protocol that achieves optimal error requires each user to send $\Omega(\min(n\varepsilon^2,d)/\log(n))$ messages, demonstrating the optimality of our message complexity up to logarithmic factors. Additionally, we study the single-message setting and design a protocol that achieves mean squared error $\mathcal{O}(dn^{d/(d+2)}\varepsilon^{-4/(d+2)})$. Moreover, we show that any single-message protocol must incur mean squared error $\Omega(dn^{d/(d+2)})$, showing that our protocol is optimal in the standard setting where $\varepsilon = \Theta(1)$. Finally, we study robustness to malicious users and show that malicious users can incur large additive error with a single shuffler.

Fast Optimal Locally Private Mean Estimation via Random Projections

We study the problem of locally private mean estimation of high-dimensional vectors in the Euclidean ball. Existing algorithms for this problem either incur sub-optimal error or have high communication and/or run-time complexity. We propose a new algorithmic framework, ProjUnit, for private mean estimation that yields algorithms that are computationally efficient, have low communication complexity, and incur optimal error up to a $1+o(1)$-factor. Our framework is deceptively simple: each randomizer projects its input to a random low-dimensional subspace, normalizes the result, and then runs an optimal algorithm such as PrivUnitG in the lower-dimensional space. In addition, we show that, by appropriately correlating the random projection matrices across devices, we can achieve fast server run-time. We mathematically analyze the error of the algorithm in terms of properties of the random projections, and study two instantiations. Lastly, our experiments for private mean estimation and private federated learning demonstrate that our algorithms empirically obtain nearly the same utility as optimal ones while having significantly lower communication and computational cost.

Online and Streaming Algorithms for Constrained $k$-Submodular Maximization

Constrained $k$-submodular maximization is a general framework that captures many discrete optimization problems such as ad allocation, influence maximization, personalized recommendation, and many others. In many of these applications, datasets are large or decisions need to be made in an online manner, which motivates the development of efficient streaming and online algorithms. In this work, we develop single-pass streaming and online algorithms for constrained $k$-submodular maximization with both monotone and general (possibly non-monotone) objectives subject to cardinality and knapsack constraints. Our algorithms achieve provable constant-factor approximation guarantees which improve upon the state of the art in almost all settings. Moreover, they are combinatorial and very efficient, and have optimal space and running time. We experimentally evaluate our algorithms on instances for ad allocation and other applications, where we observe that our algorithms are efficient and scalable, and construct solutions that are comparable in value to offline greedy algorithms.

Identification of Negative Transfers in Multitask Learning Using Surrogate Models

Multitask learning is widely used in practice to train a low-resource target task by augmenting it with multiple related source tasks. Yet, naively combining all the source tasks with a target task does not always improve the prediction performance for the target task due to negative transfers. Thus, a critical problem in multitask learning is identifying subsets of source tasks that would benefit the target task. This problem is computationally challenging since the number of subsets grows exponentially with the number of source tasks; efficient heuristics for subset selection does not always capture the relationship between task subsets and multitask learning performances. In this paper, we introduce an efficient procedure to address this problem via surrogate modeling. In surrogate modeling, we sample (random) subsets of source tasks and precompute their multitask learning performances; Then, we approximate the precomputed performances with a linear regression model that can also be used to predict the multitask performance of unseen task subsets. We show theoretically and empirically that fitting this model only requires sampling linearly many subsets in the number of source tasks. The fitted model provides a relevance score between each source task and the target task; We use the relevance scores to perform subset selection for multitask learning by thresholding. Through extensive experiments, we show that our approach predicts negative transfers from multiple source tasks to target tasks much more accurately than existing task affinity measures. Additionally, we demonstrate that for five weak supervision datasets, our approach consistently improves upon existing optimization methods for multi-task learning.

High Probability Convergence for Accelerated Stochastic Mirror Descent

In this work, we describe a generic approach to show convergence with high probability for stochastic convex optimization. In previous works, either the convergence is only in expectation or the bound depends on the diameter of the domain. Instead, we show high probability convergence with bounds depending on the initial distance to the optimal solution as opposed to the domain diameter. The algorithms use step sizes analogous to the standard settings and are universal to Lipschitz functions, smooth functions, and their linear combinations.

META-STORM: Generalized Fully-Adaptive Variance Reduced SGD for Unbounded Functions

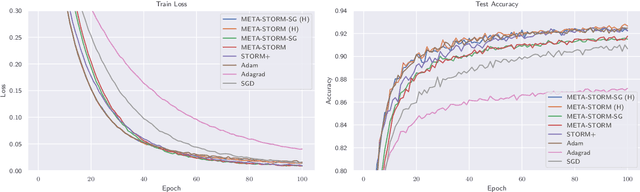
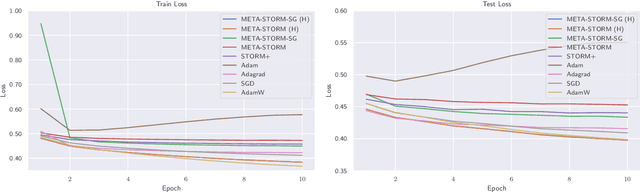
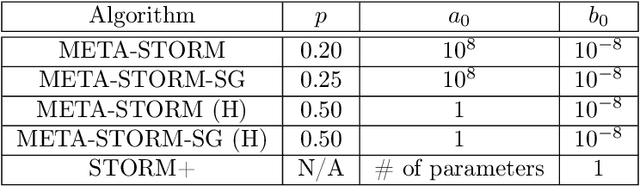
We study the application of variance reduction (VR) techniques to general non-convex stochastic optimization problems. In this setting, the recent work STORM [Cutkosky-Orabona '19] overcomes the drawback of having to compute gradients of "mega-batches" that earlier VR methods rely on. There, STORM utilizes recursive momentum to achieve the VR effect and is then later made fully adaptive in STORM+ [Levy et al., '21], where full-adaptivity removes the requirement for obtaining certain problem-specific parameters such as the smoothness of the objective and bounds on the variance and norm of the stochastic gradients in order to set the step size. However, STORM+ crucially relies on the assumption that the function values are bounded, excluding a large class of useful functions. In this work, we propose META-STORM, a generalized framework of STORM+ that removes this bounded function values assumption while still attaining the optimal convergence rate for non-convex optimization. META-STORM not only maintains full-adaptivity, removing the need to obtain problem specific parameters, but also improves the convergence rate's dependency on the problem parameters. Furthermore, META-STORM can utilize a large range of parameter settings that subsumes previous methods allowing for more flexibility in a wider range of settings. Finally, we demonstrate the effectiveness of META-STORM through experiments across common deep learning tasks. Our algorithm improves upon the previous work STORM+ and is competitive with widely used algorithms after the addition of per-coordinate update and exponential moving average heuristics.

On the Convergence of AdaGrad on $\R^{d}$: Beyond Convexity, Non-Asymptotic Rate and Acceleration

Existing analysis of AdaGrad and other adaptive methods for smooth convex optimization is typically for functions with bounded domain diameter. In unconstrained problems, previous works guarantee an asymptotic convergence rate without an explicit constant factor that holds true for the entire function class. Furthermore, in the stochastic setting, only a modified version of AdaGrad, different from the one commonly used in practice, in which the latest gradient is not used to update the stepsize, has been analyzed. Our paper aims at bridging these gaps and developing a deeper understanding of AdaGrad and its variants in the standard setting of smooth convex functions as well as the more general setting of quasar convex functions. First, we demonstrate new techniques to explicitly bound the convergence rate of the vanilla AdaGrad for unconstrained problems in both deterministic and stochastic settings. Second, we propose a variant of AdaGrad for which we can show the convergence of the last iterate, instead of the average iterate. Finally, we give new accelerated adaptive algorithms and their convergence guarantee in the deterministic setting with explicit dependency on the problem parameters, improving upon the asymptotic rate shown in previous works.

Adaptive Accelerated (Extra-)Gradient Methods with Variance Reduction

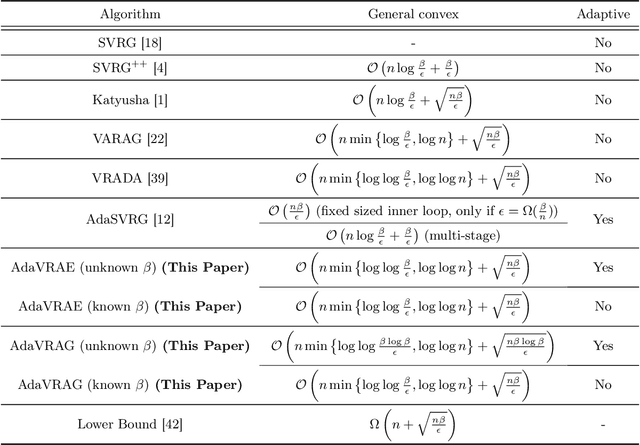
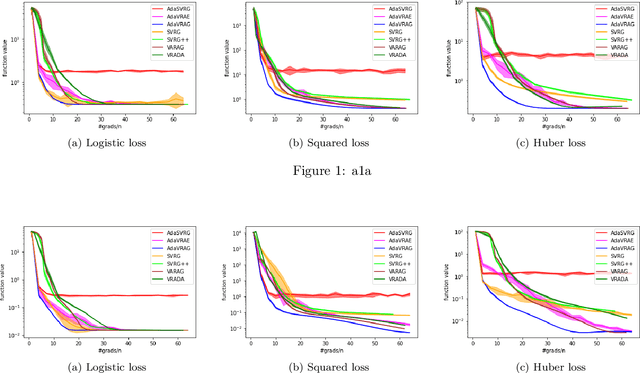
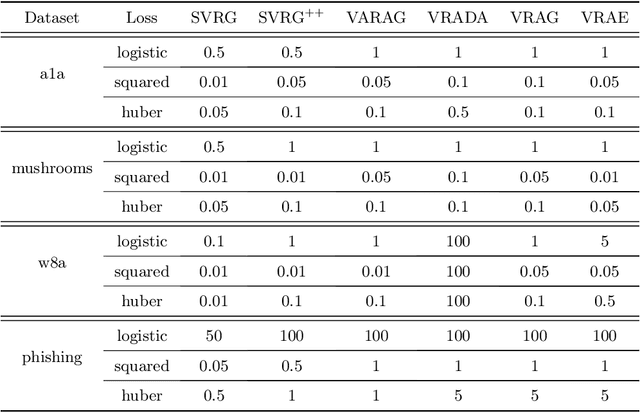
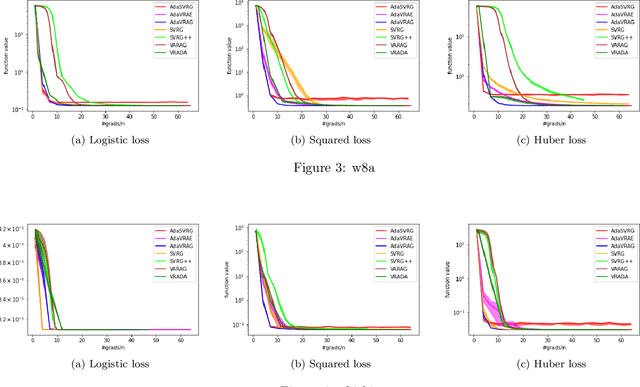
In this paper, we study the finite-sum convex optimization problem focusing on the general convex case. Recently, the study of variance reduced (VR) methods and their accelerated variants has made exciting progress. However, the step size used in the existing VR algorithms typically depends on the smoothness parameter, which is often unknown and requires tuning in practice. To address this problem, we propose two novel adaptive VR algorithms: Adaptive Variance Reduced Accelerated Extra-Gradient (AdaVRAE) and Adaptive Variance Reduced Accelerated Gradient (AdaVRAG). Our algorithms do not require knowledge of the smoothness parameter. AdaVRAE uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta}{\epsilon}}\right)$ gradient evaluations and AdaVRAG uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta\log\beta}{\epsilon}}\right)$ gradient evaluations to attain an $\mathcal{O}(\epsilon)$-suboptimal solution, where $n$ is the number of functions in the finite sum and $\beta$ is the smoothness parameter. This result matches the best-known convergence rate of non-adaptive VR methods and it improves upon the convergence of the state of the art adaptive VR method, AdaSVRG. We demonstrate the superior performance of our algorithms compared with previous methods in experiments on real-world datasets.

Locally Private $k$-Means Clustering with Constant Multiplicative Approximation and Near-Optimal Additive Error

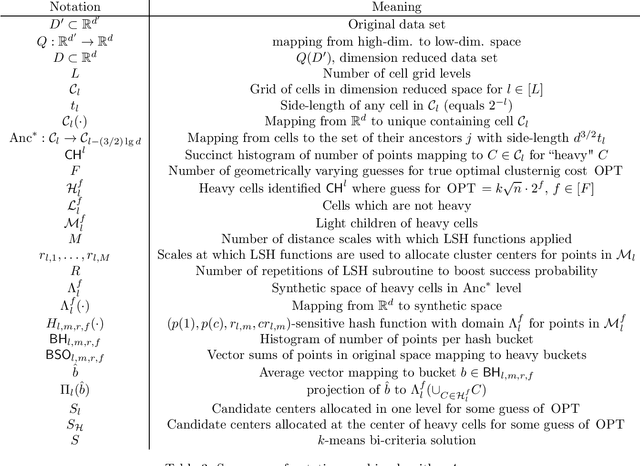
Given a data set of size $n$ in $d'$-dimensional Euclidean space, the $k$-means problem asks for a set of $k$ points (called centers) so that the sum of the $\ell_2^2$-distances between points of a given data set of size $n$ and the set of $k$ centers is minimized. Recent work on this problem in the locally private setting achieves constant multiplicative approximation with additive error $\tilde{O} (n^{1/2 + a} \cdot k \cdot \max \{\sqrt{d}, \sqrt{k} \})$ and proves a lower bound of $\Omega(\sqrt{n})$ on the additive error for any solution with a constant number of rounds. In this work we bridge the gap between the exponents of $n$ in the upper and lower bounds on the additive error with two new algorithms. Given any $\alpha>0$, our first algorithm achieves a multiplicative approximation guarantee which is at most a $(1+\alpha)$ factor greater than that of any non-private $k$-means clustering algorithm with $k^{\tilde{O}(1/\alpha^2)} \sqrt{d' n} \mbox{poly}\log n$ additive error. Given any $c>\sqrt{2}$, our second algorithm achieves $O(k^{1 + \tilde{O}(1/(2c^2-1))} \sqrt{d' n} \mbox{poly} \log n)$ additive error with constant multiplicative approximation. Both algorithms go beyond the $\Omega(n^{1/2 + a})$ factor that occurs in the additive error for arbitrarily small parameters $a$ in previous work, and the second algorithm in particular shows for the first time that it is possible to solve the locally private $k$-means problem in a constant number of rounds with constant factor multiplicative approximation and polynomial dependence on $k$ in the additive error arbitrarily close to linear.