Heuna Kim
The "something something" video database for learning and evaluating visual common sense
Jun 15, 2017
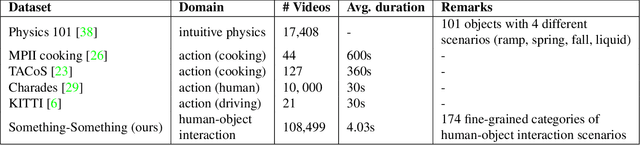

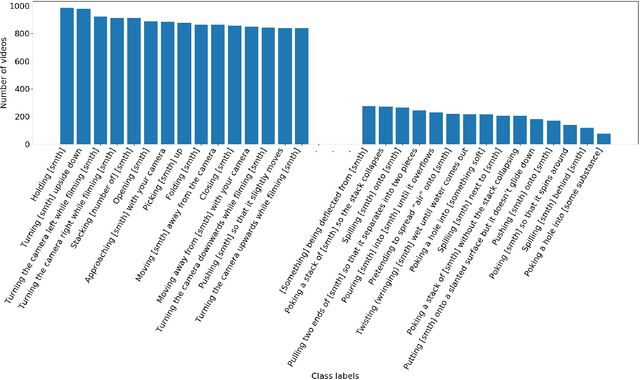
Abstract:Neural networks trained on datasets such as ImageNet have led to major advances in visual object classification. One obstacle that prevents networks from reasoning more deeply about complex scenes and situations, and from integrating visual knowledge with natural language, like humans do, is their lack of common sense knowledge about the physical world. Videos, unlike still images, contain a wealth of detailed information about the physical world. However, most labelled video datasets represent high-level concepts rather than detailed physical aspects about actions and scenes. In this work, we describe our ongoing collection of the "something-something" database of video prediction tasks whose solutions require a common sense understanding of the depicted situation. The database currently contains more than 100,000 videos across 174 classes, which are defined as caption-templates. We also describe the challenges in crowd-sourcing this data at scale.
The Shadows of a Cycle Cannot All Be Paths
Jul 09, 2015

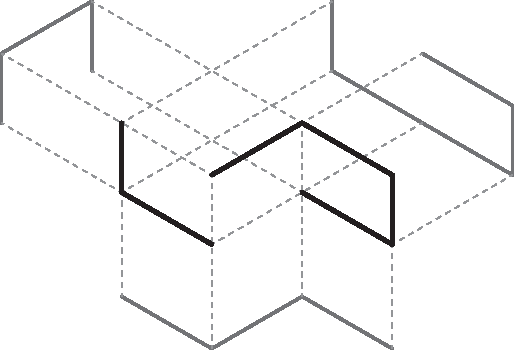
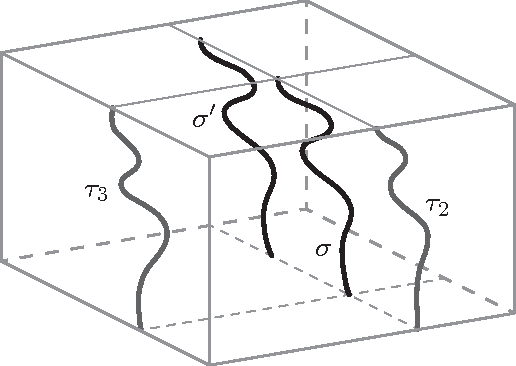
Abstract:A "shadow" of a subset $S$ of Euclidean space is an orthogonal projection of $S$ into one of the coordinate hyperplanes. In this paper we show that it is not possible for all three shadows of a cycle (i.e., a simple closed curve) in $\mathbb R^3$ to be paths (i.e., simple open curves). We also show two contrasting results: the three shadows of a path in $\mathbb R^3$ can all be cycles (although not all convex) and, for every $d\geq 1$, there exists a $d$-sphere embedded in $\mathbb R^{d+2}$ whose $d+2$ shadows have no holes (i.e., they deformation-retract onto a point).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge