The Shadows of a Cycle Cannot All Be Paths

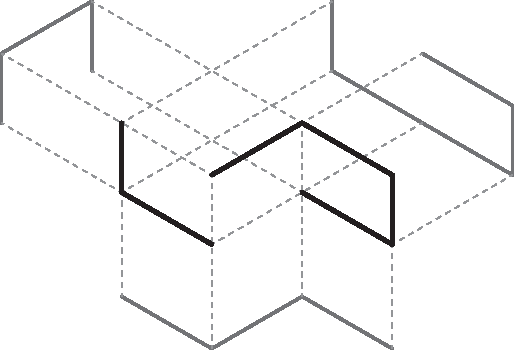
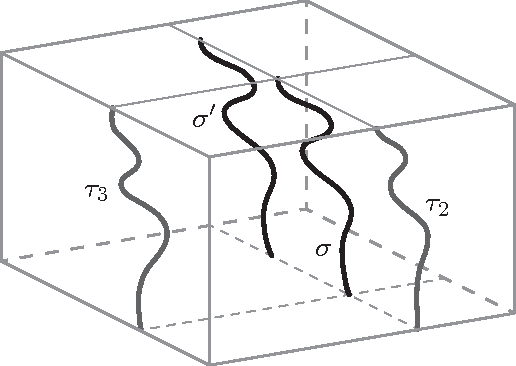
A "shadow" of a subset $S$ of Euclidean space is an orthogonal projection of $S$ into one of the coordinate hyperplanes. In this paper we show that it is not possible for all three shadows of a cycle (i.e., a simple closed curve) in $\mathbb R^3$ to be paths (i.e., simple open curves). We also show two contrasting results: the three shadows of a path in $\mathbb R^3$ can all be cycles (although not all convex) and, for every $d\geq 1$, there exists a $d$-sphere embedded in $\mathbb R^{d+2}$ whose $d+2$ shadows have no holes (i.e., they deformation-retract onto a point).

Similarity of Polygonal Curves in the Presence of Outliers

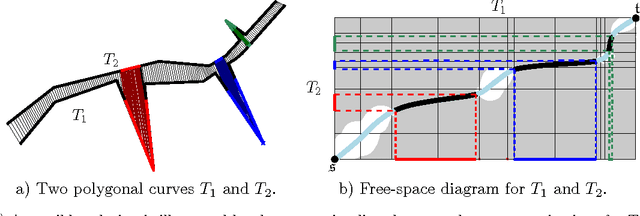
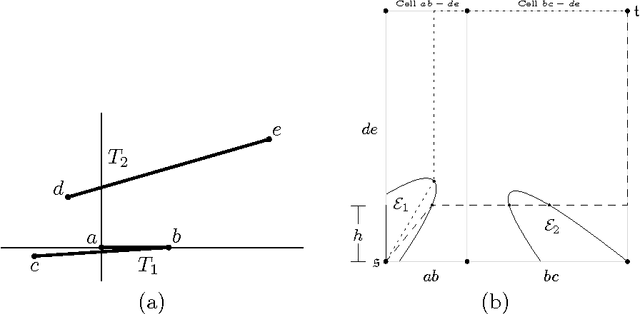
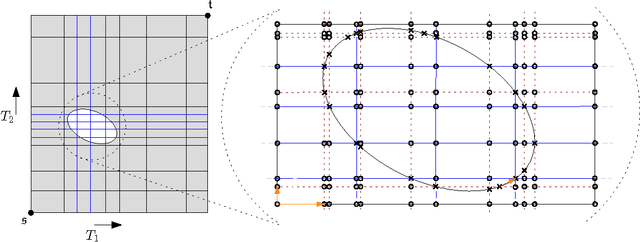
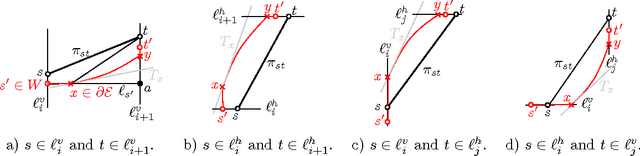
The Fr\'{e}chet distance is a well studied and commonly used measure to capture the similarity of polygonal curves. Unfortunately, it exhibits a high sensitivity to the presence of outliers. Since the presence of outliers is a frequently occurring phenomenon in practice, a robust variant of Fr\'{e}chet distance is required which absorbs outliers. We study such a variant here. In this modified variant, our objective is to minimize the length of subcurves of two polygonal curves that need to be ignored (MinEx problem), or alternately, maximize the length of subcurves that are preserved (MaxIn problem), to achieve a given Fr\'{e}chet distance. An exact solution to one problem would imply an exact solution to the other problem. However, we show that these problems are not solvable by radicals over $\mathbb{Q}$ and that the degree of the polynomial equations involved is unbounded in general. This motivates the search for approximate solutions. We present an algorithm, which approximates, for a given input parameter $\delta$, optimal solutions for the \MinEx\ and \MaxIn\ problems up to an additive approximation error $\delta$ times the length of the input curves. The resulting running time is upper bounded by $\mathcal{O} \left(\frac{n^3}{\delta} \log \left(\frac{n}{\delta} \right)\right)$, where $n$ is the complexity of the input polygonal curves.