One-Step Offline Distillation of Diffusion-based Models via Koopman Modeling

Diffusion-based generative models have demonstrated exceptional performance, yet their iterative sampling procedures remain computationally expensive. A prominent strategy to mitigate this cost is distillation, with offline distillation offering particular advantages in terms of efficiency, modularity, and flexibility. In this work, we identify two key observations that motivate a principled distillation framework: (1) while diffusion models have been viewed through the lens of dynamical systems theory, powerful and underexplored tools can be further leveraged; and (2) diffusion models inherently impose structured, semantically coherent trajectories in latent space. Building on these observations, we introduce the Koopman Distillation Model KDM, a novel offline distillation approach grounded in Koopman theory-a classical framework for representing nonlinear dynamics linearly in a transformed space. KDM encodes noisy inputs into an embedded space where a learned linear operator propagates them forward, followed by a decoder that reconstructs clean samples. This enables single-step generation while preserving semantic fidelity. We provide theoretical justification for our approach: (1) under mild assumptions, the learned diffusion dynamics admit a finite-dimensional Koopman representation; and (2) proximity in the Koopman latent space correlates with semantic similarity in the generated outputs, allowing for effective trajectory alignment. Empirically, KDM achieves state-of-the-art performance across standard offline distillation benchmarks, improving FID scores by up to 40% in a single generation step. All implementation details and code for the experimental setups are provided in our GitHub - https://github.com/azencot-group/KDM, or in our project page - https://sites.google.com/view/koopman-distillation-model.

A Multi-Task Learning Approach to Linear Multivariate Forecasting

Accurate forecasting of multivariate time series data is important in many engineering and scientific applications. Recent state-of-the-art works ignore the inter-relations between variates, using their model on each variate independently. This raises several research questions related to proper modeling of multivariate data. In this work, we propose to view multivariate forecasting as a multi-task learning problem, facilitating the analysis of forecasting by considering the angle between task gradients and their balance. To do so, we analyze linear models to characterize the behavior of tasks. Our analysis suggests that tasks can be defined by grouping similar variates together, which we achieve via a simple clustering that depends on correlation-based similarities. Moreover, to balance tasks, we scale gradients with respect to their prediction error. Then, each task is solved with a linear model within our MTLinear framework. We evaluate our approach on challenging benchmarks in comparison to strong baselines, and we show it obtains on-par or better results on multivariate forecasting problems. The implementation is available at: https://github.com/azencot-group/MTLinear

VNT-Net: Rotational Invariant Vector Neuron Transformers

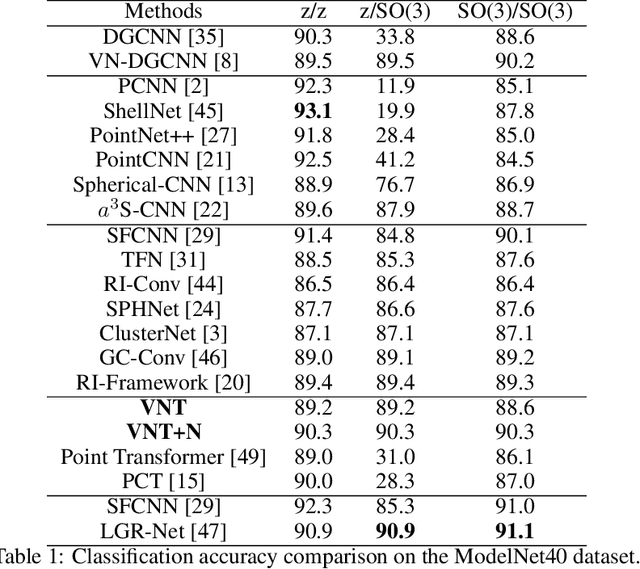
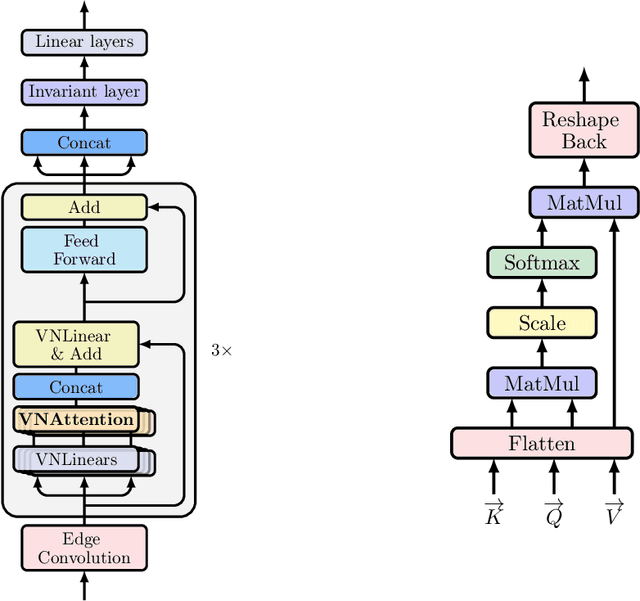
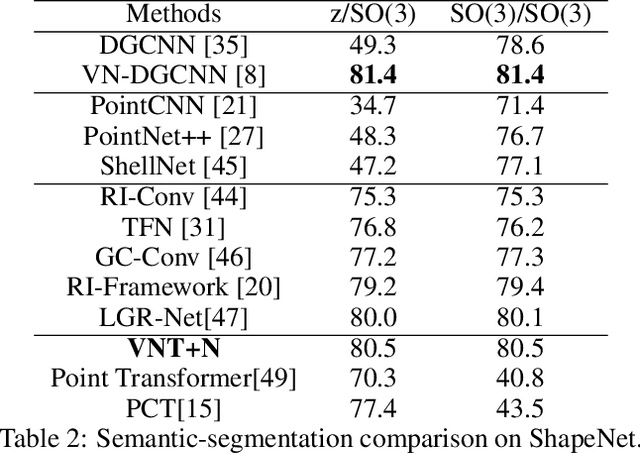
Learning 3D point sets with rotational invariance is an important and challenging problem in machine learning. Through rotational invariant architectures, 3D point cloud neural networks are relieved from requiring a canonical global pose and from exhaustive data augmentation with all possible rotations. In this work, we introduce a rotational invariant neural network by combining recently introduced vector neurons with self-attention layers to build a point cloud vector neuron transformer network (VNT-Net). Vector neurons are known for their simplicity and versatility in representing SO(3) actions and are thereby incorporated in common neural operations. Similarly, Transformer architectures have gained popularity and recently were shown successful for images by applying directly on sequences of image patches and achieving superior performance and convergence. In order to benefit from both worlds, we combine the two structures by mainly showing how to adapt the multi-headed attention layers to comply with vector neurons operations. Through this adaptation attention layers become SO(3) and the overall network becomes rotational invariant. Experiments demonstrate that our network efficiently handles 3D point cloud objects in arbitrary poses. We also show that our network achieves higher accuracy when compared to related state-of-the-art methods and requires less training due to a smaller number of hyperparameters in common classification and segmentation tasks.