Multi-Robot Task Allocation -- Complexity and Approximation

Multi-robot task allocation is one of the most fundamental classes of problems in robotics and is crucial for various real-world robotic applications such as search, rescue and area exploration. We consider the Single-Task robots and Multi-Robot tasks Instantaneous Assignment (ST-MR-IA) setting where each task requires at least a certain number of robots and each robot can work on at most one task and incurs an operational cost for each task. Our aim is to consider a natural computational problem of allocating robots to complete the maximum number of tasks subject to budget constraints. We consider budget constraints of three different kinds: (1) total budget, (2) task budget, and (3) robot budget. We provide a detailed complexity analysis including results on approximations as well as polynomial-time algorithms for the general setting and important restricted settings.

A characterization of proportionally representative committees

A well-known axiom for proportional representation is Proportionality of Solid Coalitions (PSC). We characterize committees satisfying PSC as possible outcomes of the Minimal Demand rule, which generalizes an approach pioneered by Michael Dummett.

From Matching with Diversity Constraints to Matching with Regional Quotas

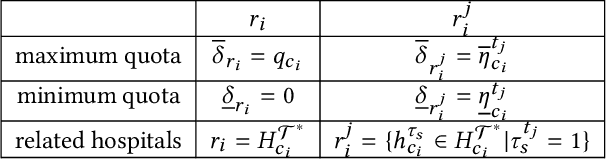
In the past few years, several new matching models have been proposed and studied that take into account complex distributional constraints. Relevant lines of work include (1) school choice with diversity constraints where students have (possibly overlapping) types and (2) hospital-doctor matching where various regional quotas are imposed. In this paper, we present a polynomial-time reduction to transform an instance of (1) to an instance of (2) and we show how the feasibility and stability of corresponding matchings are preserved under the reduction. Our reduction provides a formal connection between two important strands of work on matching with distributional constraints. We then apply the reduction in two ways. Firstly, we show that it is NP-complete to check whether a feasible and stable outcome for (1) exists. Due to our reduction, these NP-completeness results carry over to setting (2). In view of this, we help unify some of the results that have been presented in the literature. Secondly, if we have positive results for (2), then we have corresponding results for (1). One key conclusion of our results is that further developments on axiomatic and algorithmic aspects of hospital-doctor matching with regional quotas will result in corresponding results for school choice with diversity constraints.

Facility Location Problem with Capacity Constraints: Algorithmic and Mechanism Design Perspectives

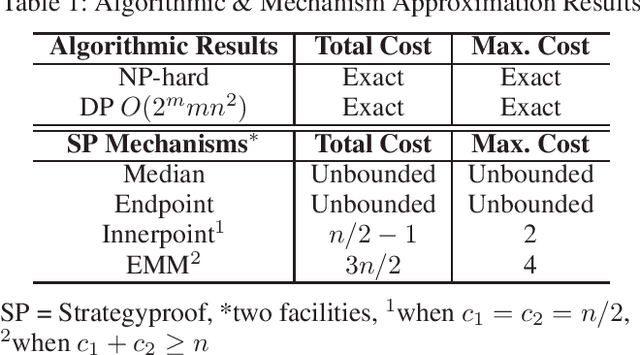
We consider the facility location problem in the one-dimensional setting where each facility can serve a limited number of agents from the algorithmic and mechanism design perspectives. From the algorithmic perspective, we prove that the corresponding optimization problem, where the goal is to locate facilities to minimize either the total cost to all agents or the maximum cost of any agent is NP-hard. However, we show that the problem is fixed-parameter tractable, and the optimal solution can be computed in polynomial time whenever the number of facilities is bounded, or when all facilities have identical capacities. We then consider the problem from a mechanism design perspective where the agents are strategic and need not reveal their true locations. We show that several natural mechanisms studied in the uncapacitated setting either lose strategyproofness or a bound on the solution quality for the total or maximum cost objective. We then propose new mechanisms that are strategyproof and achieve approximation guarantees that almost match the lower bounds.

Almost Group Envy-free Allocation of Indivisible Goods and Chores

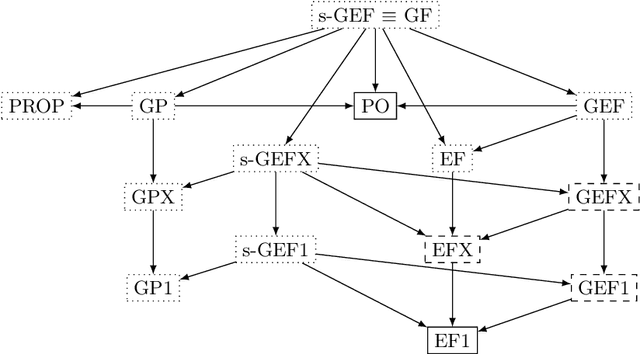
We consider a multi-agent resource allocation setting in which an agent's utility may decrease or increase when an item is allocated. We take the group envy-freeness concept that is well-established in the literature and present stronger and relaxed versions that are especially suitable for the allocation of indivisible items. Of particular interest is a concept called group envy-freeness up to one item (GEF1). We then present a clear taxonomy of the fairness concepts. We study which fairness concepts guarantee the existence of a fair allocation under which preference domain. For two natural classes of additive utilities, we design polynomial-time algorithms to compute a GEF1 allocation. We also prove that checking whether a given allocation satisfies GEF1 is coNP-complete when there are either only goods, only chores or both.

The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity

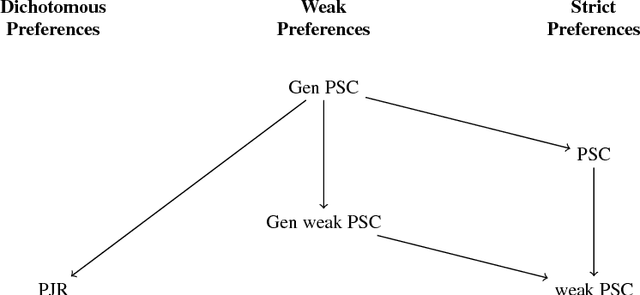
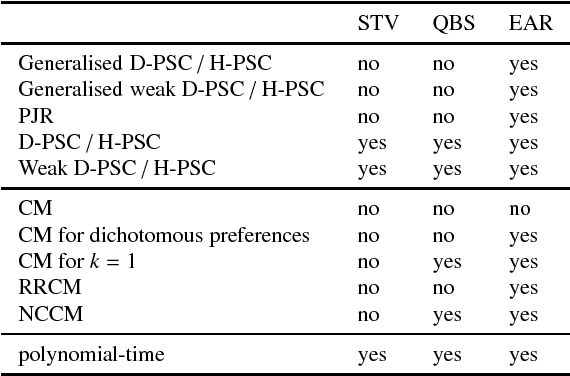
Proportional representation (PR) is often discussed in voting settings as a major desideratum. For the past century or so, it is common both in practice and in the academic literature to jump to single transferable vote (STV) as the solution for achieving PR. Some of the most prominent electoral reform movements around the globe are pushing for the adoption of STV. It has been termed a major open problem to design a voting rule that satisfies the same PR properties as STV and better monotonicity properties. In this paper, we first present a taxonomy of proportional representation axioms for general weak order preferences, some of which generalise and strengthen previously introduced concepts. We then present a rule called Expanding Approvals Rule (EAR) that satisfies properties stronger than the central PR axiom satisfied by STV, can handle indifferences in a convenient and computationally efficient manner, and also satisfies better candidate monotonicity properties. In view of this, our proposed rule seems to be a compelling solution for achieving proportional representation in voting settings.

Mechanism Design without Money for Common Goods

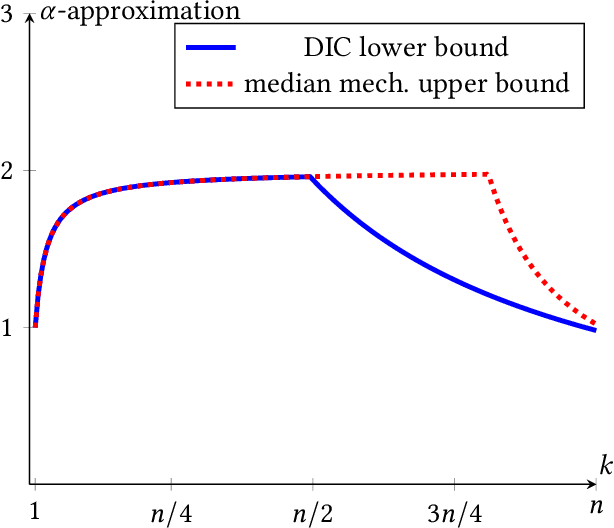
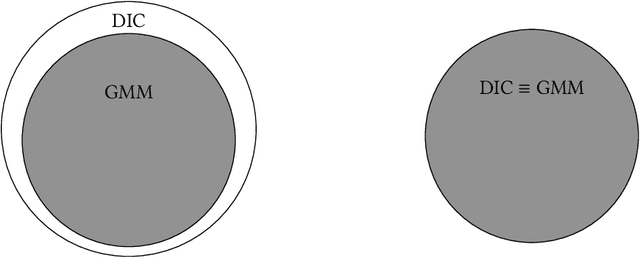
We initiate the study of mechanism design without money for common goods. Our model captures a variation of the well-known one-dimensional facility location problem if the facility is assumed to have a capacity constraint $k<n$ where $n$ is the population size. This new model introduces a richer game-theoretic context compared to the classical facility location, or public goods, problem. Our key result contributes a novel perspective relating to the "major open question" (Barbar\`a et al., 1998) posed by Border and Jordan (1983) by showing the equivalence of dominant strategy incentive compatible (DIC) mechanisms for common goods and the family of Generalized Median Mechanisms (GMMs). This equivalence does not hold in the public goods setting and, by situating GMMs in this broader game-theoretic context, is the first complete characterization of GMMs in terms of purely strategic properties. We then characterize lower bounds of the welfare approximation ratio across all DIC mechanisms and identify a DIC mechanism which attains this lower bound when $k<\lceil (n+1)/2\rceil$ and $k=n$. Finally, we analyze the approximation ratio when the property of DIC is weakened to ex post incentive compatibility.

A Rule for Committee Selection with Soft Diversity Constraints

Committee selection with diversity or distributional constraints is a ubiquitous problem. However, many of the formal approaches proposed so far have certain drawbacks including (1) computationally intractability in general, and (2) inability to suggest a solution for certain instances where the hard constraints cannot be met. We propose a practical and polynomial-time algorithm for diverse committee selection that draws on the idea of using soft bounds and satisfies natural axioms.

Computing and Testing Pareto Optimal Committees

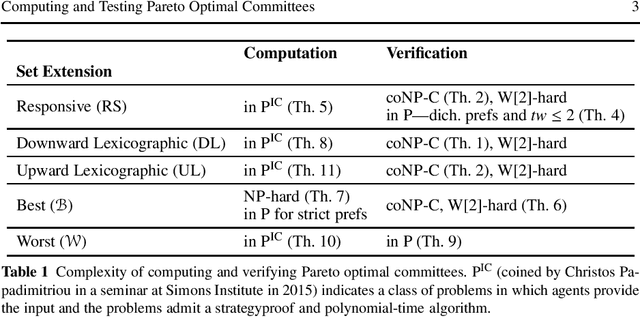
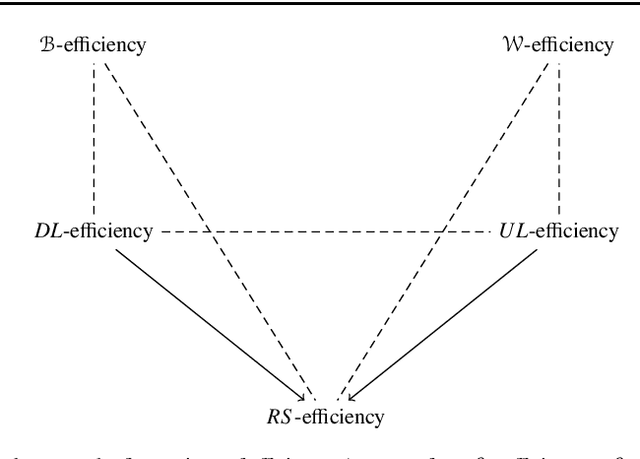
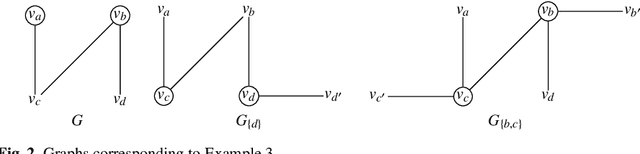
Selecting a set of alternatives based on the preferences of agents is an important problem in committee selection and beyond. Among the various criteria put forth for the desirability of a committee, Pareto optimality is a minimal and important requirement. As asking agents to specify their preferences over exponentially many subsets of alternatives is practically infeasible, we assume that each agent specifies a weak order on single alternatives, from which a preference relation over subsets is derived using some preference extension. We consider five prominent extensions (responsive, downward lexicographic, upward lexicographic, best, and worst). For each of them, we consider the corresponding Pareto optimality notion, and we study the complexity of computing and verifying Pareto optimal outcomes. We also consider strategic issues: for four of the set extensions, we present a linear-time, Pareto optimal and strategyproof algorithm that even works for weak preferences.

Sub-committee Approval Voting and Generalised Justified Representation Axioms

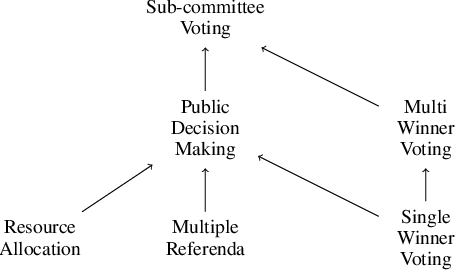
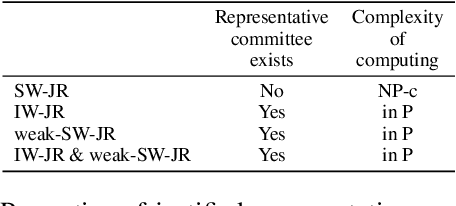
Social choice is replete with various settings including single-winner voting, multi-winner voting, probabilistic voting, multiple referenda, and public decision making. We study a general model of social choice called Sub-Committee Voting (SCV) that simultaneously generalizes these settings. We then focus on sub-committee voting with approvals and propose extensions of the justified representation axioms that have been considered for proportional representation in approval-based committee voting. We study the properties and relations of these axioms. For each of the axioms, we analyse whether a representative committee exists and also examine the complexity of computing and verifying such a committee.