Lithological Controls on the Permeability of Geologic Faults: Surrogate Modeling and Sensitivity Analysis

Fault zones exhibit complex and heterogeneous permeability structures influenced by stratigraphic, compositional, and structural factors, making them critical yet uncertain components in subsurface flow modeling. In this study, we investigate how lithological controls influence fault permeability using the PREDICT framework: a probabilistic workflow that couples stochastic fault geometry generation, physically constrained material placement, and flow-based upscaling. The flow-based upscaling step, however, is a very computationally expensive component of the workflow and presents a major bottleneck that makes global sensitivity analysis (GSA) intractable, as it requires millions of model evaluations. To overcome this challenge, we develop a neural network surrogate to emulate the flow-based upscaling step. This surrogate model dramatically reduces the computational cost while maintaining high accuracy, thereby making GSA feasible. The surrogate-model-enabled GSA reveals new insights into the effects of lithological controls on fault permeability. In addition to identifying dominant parameters and negligible ones, the analysis uncovers significant nonlinear interactions between parameters that cannot be captured by traditional local sensitivity methods.

Learning Nonautonomous Systems via Dynamic Mode Decomposition

We present a data-driven learning approach for unknown nonautonomous dynamical systems with time-dependent inputs based on dynamic mode decomposition (DMD). To circumvent the difficulty of approximating the time-dependent Koopman operators for nonautonomous systems, a modified system derived from local parameterization of the external time-dependent inputs is employed as an approximation to the original nonautonomous system. The modified system comprises a sequence of local parametric systems, which can be well approximated by a parametric surrogate model using our previously proposed framework for dimension reduction and interpolation in parameter space (DRIPS). The offline step of DRIPS relies on DMD to build a linear surrogate model, endowed with reduced-order bases (ROBs), for the observables mapped from training data. Then the offline step constructs a sequence of iterative parametric surrogate models from interpolations on suitable manifolds, where the target/test parameter points are specified by the local parameterization of the test external time-dependent inputs. We present a number of numerical examples to demonstrate the robustness of our method and compare its performance with deep neural networks in the same settings.

Machine Learning in Heterogeneous Porous Materials

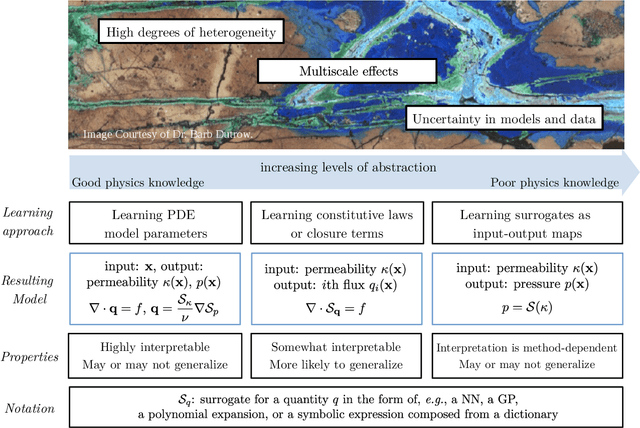
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.