Robust Model Predictive Control Design for Autonomous Vehicles with Perception-based Observers

This paper presents a robust model predictive control (MPC) framework that explicitly addresses the non-Gaussian noise inherent in deep learning-based perception modules used for state estimation. Recognizing that accurate uncertainty quantification of the perception module is essential for safe feedback control, our approach departs from the conventional assumption of zero-mean noise quantification of the perception error. Instead, it employs set-based state estimation with constrained zonotopes to capture biased, heavy-tailed uncertainties while maintaining bounded estimation errors. To improve computational efficiency, the robust MPC is reformulated as a linear program (LP), using a Minkowski-Lyapunov-based cost function with an added slack variable to prevent degenerate solutions. Closed-loop stability is ensured through Minkowski-Lyapunov inequalities and contractive zonotopic invariant sets. The largest stabilizing terminal set and its corresponding feedback gain are then derived via an ellipsoidal approximation of the zonotopes. The proposed framework is validated through both simulations and hardware experiments on an omnidirectional mobile robot along with a camera and a convolutional neural network-based perception module implemented within a ROS2 framework. The results demonstrate that the perception-aware MPC provides stable and accurate control performance under heavy-tailed noise conditions, significantly outperforming traditional Gaussian-noise-based designs in terms of both state estimation error bounding and overall control performance.

SAFE--MA--RRT: Multi-Agent Motion Planning with Data-Driven Safety Certificates

This paper proposes a fully data-driven motion-planning framework for homogeneous linear multi-agent systems that operate in shared, obstacle-filled workspaces without access to explicit system models. Each agent independently learns its closed-loop behavior from experimental data by solving convex semidefinite programs that generate locally invariant ellipsoids and corresponding state-feedback gains. These ellipsoids, centered along grid-based waypoints, certify the dynamic feasibility of short-range transitions and define safe regions of operation. A sampling-based planner constructs a tree of such waypoints, where transitions are allowed only when adjacent ellipsoids overlap, ensuring invariant-to-invariant transitions and continuous safety. All agents expand their trees simultaneously and are coordinated through a space-time reservation table that guarantees inter-agent safety by preventing simultaneous occupancy and head-on collisions. Each successful edge in the tree is equipped with its own local controller, enabling execution without re-solving optimization problems at runtime. The resulting trajectories are not only dynamically feasible but also provably safe with respect to both environmental constraints and inter-agent collisions. Simulation results demonstrate the effectiveness of the approach in synthesizing synchronized, safe trajectories for multiple agents under shared dynamics and constraints, using only data and convex optimization tools.

Data-Driven Motion Planning for Uncertain Nonlinear Systems

This paper proposes a data-driven motion-planning framework for nonlinear systems that constructs a sequence of overlapping invariant polytopes. Around each randomly sampled waypoint, the algorithm identifies a convex admissible region and solves data-driven linear-matrix-inequality problems to learn several ellipsoidal invariant sets together with their local state-feedback gains. The convex hull of these ellipsoids, still invariant under a piece-wise-affine controller obtained by interpolating the gains, is then approximated by a polytope. Safe transitions between nodes are ensured by verifying the intersection of consecutive convex-hull polytopes and introducing an intermediate node for a smooth transition. Control gains are interpolated in real time via simplex-based interpolation, keeping the state inside the invariant polytopes throughout the motion. Unlike traditional approaches that rely on system dynamics models, our method requires only data to compute safe regions and design state-feedback controllers. The approach is validated through simulations, demonstrating the effectiveness of the proposed method in achieving safe, dynamically feasible paths for complex nonlinear systems.

Risk-Aware Safe Reinforcement Learning for Control of Stochastic Linear Systems

This paper presents a risk-aware safe reinforcement learning (RL) control design for stochastic discrete-time linear systems. Rather than using a safety certifier to myopically intervene with the RL controller, a risk-informed safe controller is also learned besides the RL controller, and the RL and safe controllers are combined together. Several advantages come along with this approach: 1) High-confidence safety can be certified without relying on a high-fidelity system model and using limited data available, 2) Myopic interventions and convergence to an undesired equilibrium can be avoided by deciding on the contribution of two stabilizing controllers, and 3) highly efficient and computationally tractable solutions can be provided by optimizing over a scalar decision variable and linear programming polyhedral sets. To learn safe controllers with a large invariant set, piecewise affine controllers are learned instead of linear controllers. To this end, the closed-loop system is first represented using collected data, a decision variable, and noise. The effect of the decision variable on the variance of the safe violation of the closed-loop system is formalized. The decision variable is then designed such that the probability of safety violation for the learned closed-loop system is minimized. It is shown that this control-oriented approach reduces the data requirements and can also reduce the variance of safety violations. Finally, to integrate the safe and RL controllers, a new data-driven interpolation technique is introduced. This method aims to maintain the RL agent's optimal implementation while ensuring its safety within environments characterized by noise. The study concludes with a simulation example that serves to validate the theoretical results.

Direct Data Driven Control Using Noisy Measurements

This paper presents a novel direct data-driven control framework for solving the linear quadratic regulator (LQR) under disturbances and noisy state measurements. The system dynamics are assumed unknown, and the LQR solution is learned using only a single trajectory of noisy input-output data while bypassing system identification. Our approach guarantees mean-square stability (MSS) and optimal performance by leveraging convex optimization techniques that incorporate noise statistics directly into the controller synthesis. First, we establish a theoretical result showing that the MSS of an uncertain data-driven system implies the MSS of the true closed-loop system. Building on this, we develop a robust stability condition using linear matrix inequalities (LMIs) that yields a stabilizing controller gain from noisy measurements. Finally, we formulate a data-driven LQR problem as a semidefinite program (SDP) that computes an optimal gain, minimizing the steady-state covariance. Extensive simulations on benchmark systems -- including a rotary inverted pendulum and an active suspension system -- demonstrate the superior robustness and accuracy of our method compared to existing data-driven LQR approaches. The proposed framework offers a practical and theoretically grounded solution for controller design in noise-corrupted environments where system identification is infeasible.

Assured Learning-enabled Autonomy: A Metacognitive Reinforcement Learning Framework

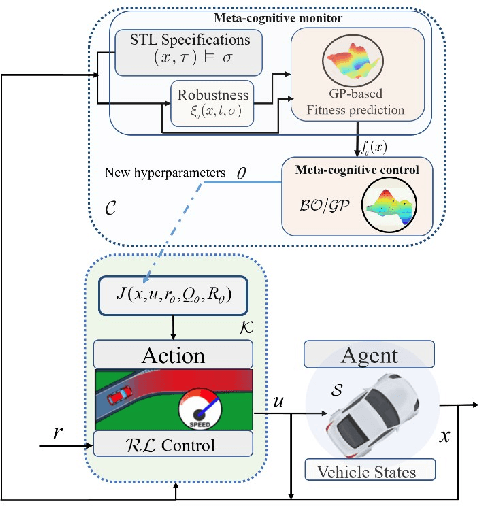
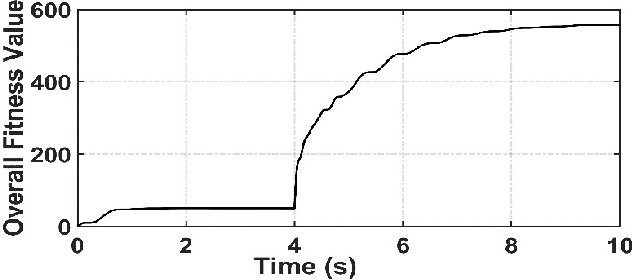
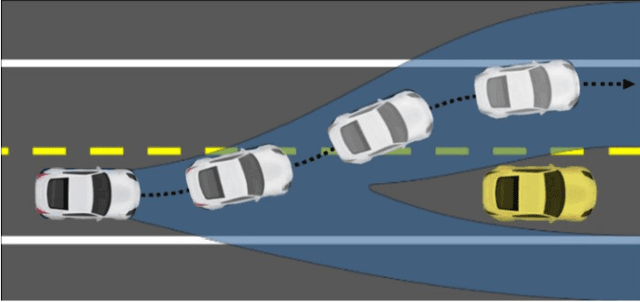
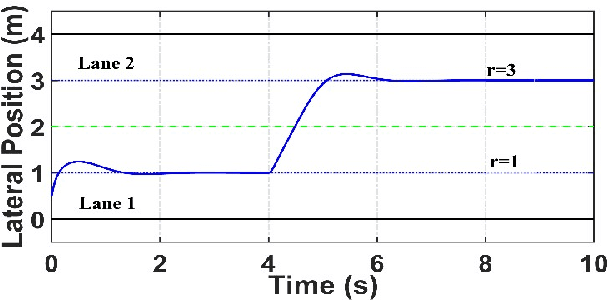
Reinforcement learning (RL) agents with pre-specified reward functions cannot provide guaranteed safety across variety of circumstances that an uncertain system might encounter. To guarantee performance while assuring satisfaction of safety constraints across variety of circumstances, an assured autonomous control framework is presented in this paper by empowering RL algorithms with metacognitive learning capabilities. More specifically, adapting the reward function parameters of the RL agent is performed in a metacognitive decision-making layer to assure the feasibility of RL agent. That is, to assure that the learned policy by the RL agent satisfies safety constraints specified by signal temporal logic while achieving as much performance as possible. The metacognitive layer monitors any possible future safety violation under the actions of the RL agent and employs a higher-layer Bayesian RL algorithm to proactively adapt the reward function for the lower-layer RL agent. To minimize the higher-layer Bayesian RL intervention, a fitness function is leveraged by the metacognitive layer as a metric to evaluate success of the lower-layer RL agent in satisfaction of safety and liveness specifications, and the higher-layer Bayesian RL intervenes only if there is a risk of lower-layer RL failure. Finally, a simulation example is provided to validate the effectiveness of the proposed approach.

Observer-based Adaptive Optimal Output Containment Control problem of Linear Heterogeneous Multi-agent Systems with Relative Output Measurements

This paper develops an optimal relative output-feedback based solution to the containment control problem of linear heterogeneous multi-agent systems. A distributed optimal control protocol is presented for the followers to not only assure that their outputs fall into the convex hull of the leaders' output (i.e., the desired or safe region), but also optimizes their transient performance. The proposed optimal control solution is composed of a feedback part, depending of the followers' state, and a feed-forward part, depending on the convex hull of the leaders' state. To comply with most real-world applications, the feedback and feed-forward states are assumed to be unavailable and are estimated using two distributed observers. That is, since the followers cannot directly sense their absolute states, a distributed observer is designed that uses only relative output measurements with respect to their neighbors (measured for example by using range sensors in robotic) and the information which is broadcasted by their neighbors to estimate their states. Moreover, another adaptive distributed observer is designed that uses exchange of information between followers over a communication network to estimate the convex hull of the leaders' state. The proposed observer relaxes the restrictive requirement of knowing the complete knowledge of the leaders' dynamics by all followers. An off-policy reinforcement learning algorithm on an actor-critic structure is next developed to solve the optimal containment control problem online, using relative output measurements and without requirement of knowing the leaders' dynamics by all followers. Finally, the theoretical results are verified by numerical simulations.