Uncertainty Quantification for Transport in Porous media using Parameterized Physics Informed neural Networks

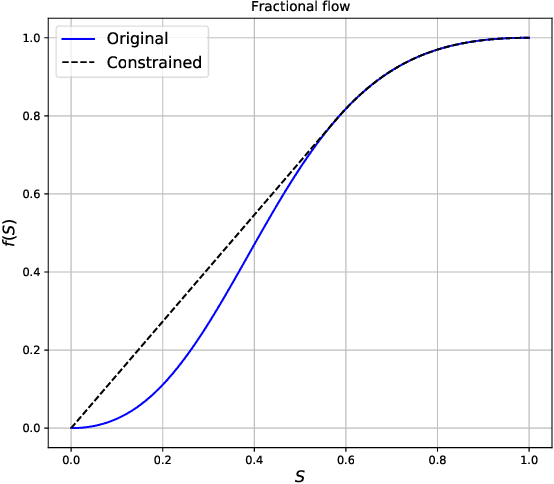
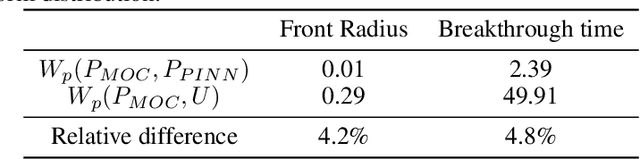
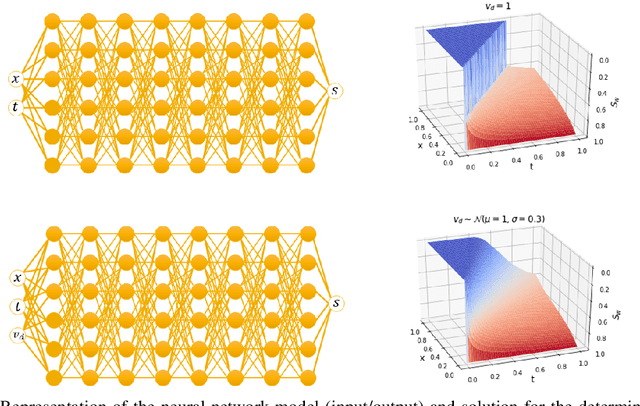
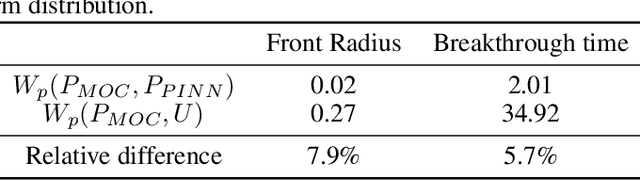
We present a Parametrization of the Physics Informed Neural Network (P-PINN) approach to tackle the problem of uncertainty quantification in reservoir engineering problems. We demonstrate the approach with the immiscible two phase flow displacement (Buckley-Leverett problem) in heterogeneous porous medium. The reservoir properties (porosity, permeability) are treated as random variables. The distribution of these properties can affect dynamic properties such as the fluids saturation, front propagation speed or breakthrough time. We explore and use to our advantage the ability of networks to interpolate complex high dimensional functions. We observe that the additional dimensions resulting from a stochastic treatment of the partial differential equations tend to produce smoother solutions on quantities of interest (distributions parameters) which is shown to improve the performance of PINNS. We show that provided a proper parameterization of the uncertainty space, PINN can produce solutions that match closely both the ensemble realizations and the stochastic moments. We demonstrate applications for both homogeneous and heterogeneous fields of properties. We are able to solve problems that can be challenging for classical methods. This approach gives rise to trained models that are both more robust to variations in the input space and can compete in performance with traditional stochastic sampling methods.

Machine Learning in Heterogeneous Porous Materials

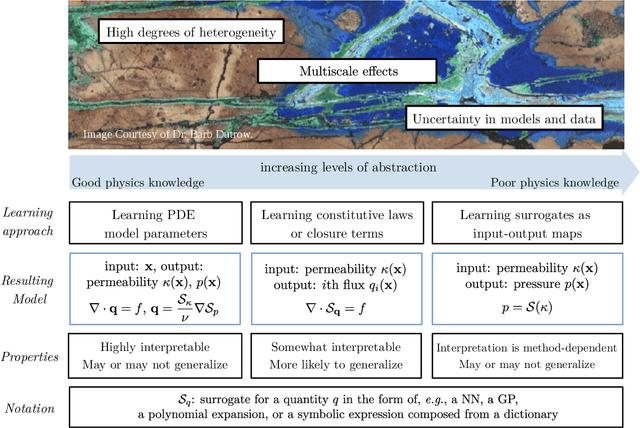
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Physics Informed Deep Learning for Transport in Porous Media. Buckley Leverett Problem

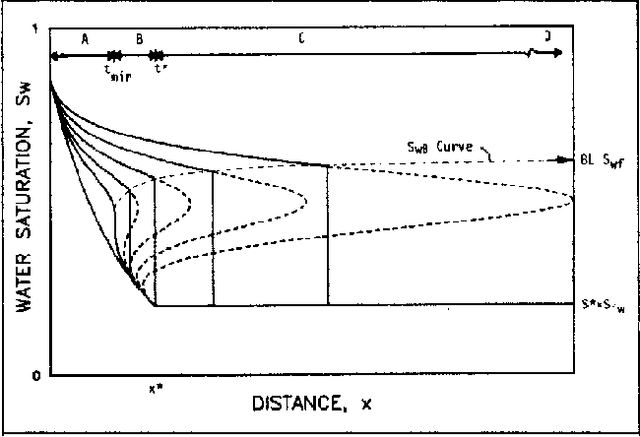
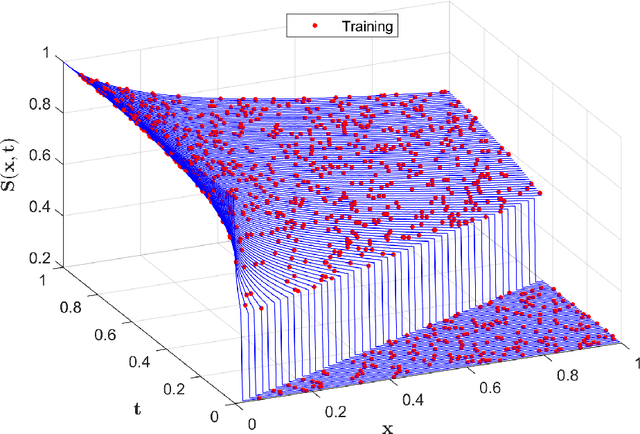
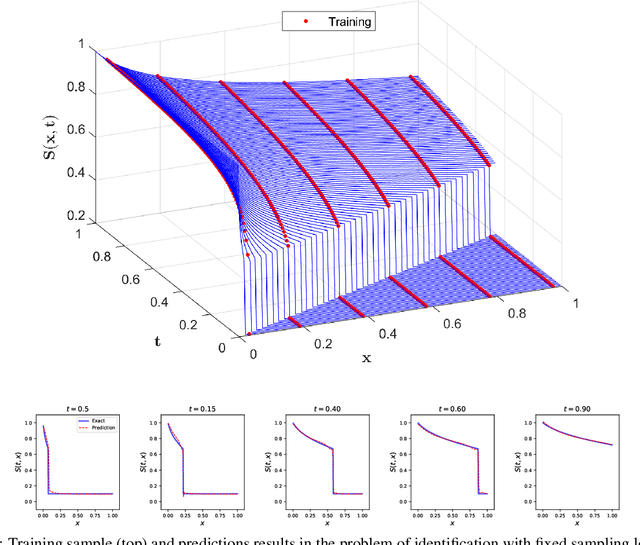
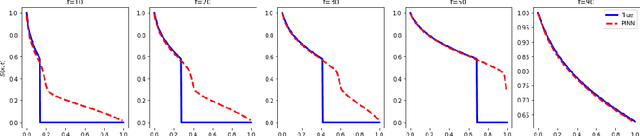
We present a new hybrid physics-based machine-learning approach to reservoir modeling. The methodology relies on a series of deep adversarial neural network architecture with physics-based regularization. The network is used to simulate the dynamic behavior of physical quantities (i.e. saturation) subject to a set of governing laws (e.g. mass conservation) and corresponding boundary and initial conditions. A residual equation is formed from the governing partial-differential equation and used as part of the training. Derivatives of the estimated physical quantities are computed using automatic differentiation algorithms. This allows the model to avoid overfitting, by reducing the variance and permits extrapolation beyond the range of the training data including uncertainty implicitely derived from the distribution output of the generative adversarial networks. The approach is used to simulate a 2 phase immiscible transport problem (Buckley Leverett). From a very limited dataset, the model learns the parameters of the governing equation and is able to provide an accurate physical solution, both in terms of shock and rarefaction. We demonstrate how this method can be applied in the context of a forward simulation for continuous problems. The use of these models for the inverse problem is also presented, where the model simultaneously learns the physical laws and determines key uncertainty subsurface parameters. The proposed methodology is a simple and elegant way to instill physical knowledge to machine-learning algorithms. This alleviates the two most significant shortcomings of machine-learning algorithms: the requirement for large datasets and the reliability of extrapolation. The principles presented in this paper can be generalized in innumerable ways in the future and should lead to a new class of algorithms to solve both forward and inverse physical problems.