Mechanistic Insights into Grokking from the Embedding Layer

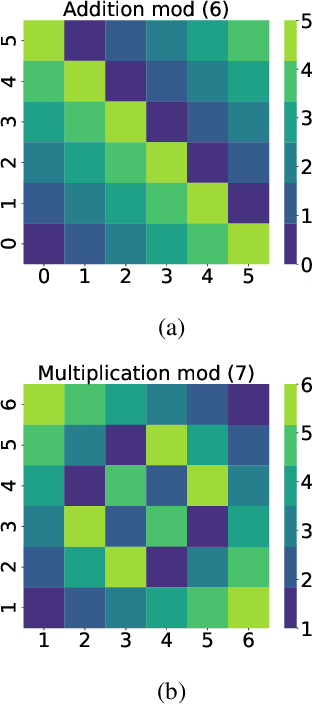
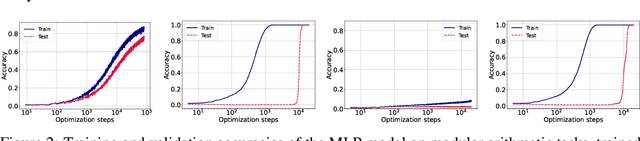
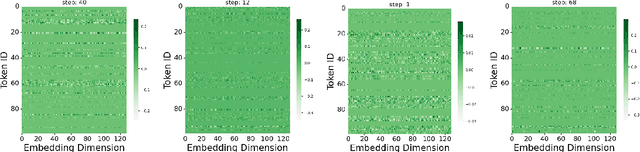
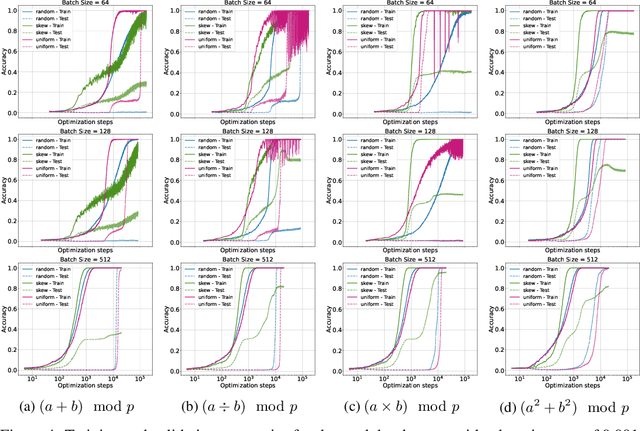
Grokking, a delayed generalization in neural networks after perfect training performance, has been observed in Transformers and MLPs, but the components driving it remain underexplored. We show that embeddings are central to grokking: introducing them into MLPs induces delayed generalization in modular arithmetic tasks, whereas MLPs without embeddings can generalize immediately. Our analysis identifies two key mechanisms: (1) Embedding update dynamics, where rare tokens stagnate due to sparse gradient updates and weight decay, and (2) Bilinear coupling, where the interaction between embeddings and downstream weights introduces saddle points and increases sensitivity to initialization. To confirm these mechanisms, we investigate frequency-aware sampling, which balances token updates by minimizing gradient variance, and embedding-specific learning rates, derived from the asymmetric curvature of the bilinear loss landscape. We prove that an adaptive learning rate ratio, \(\frac{\eta_E}{\eta_W} \propto \frac{\sigma_{\max}(E)}{\sigma_{\max}(W)} \cdot \frac{f_W}{f_E}\), mitigates bilinear coupling effects, accelerating convergence. Our methods not only improve grokking dynamics but also extend to broader challenges in Transformer optimization, where bilinear interactions hinder efficient training.

Number Representations in LLMs: A Computational Parallel to Human Perception

Humans are believed to perceive numbers on a logarithmic mental number line, where smaller values are represented with greater resolution than larger ones. This cognitive bias, supported by neuroscience and behavioral studies, suggests that numerical magnitudes are processed in a sublinear fashion rather than on a uniform linear scale. Inspired by this hypothesis, we investigate whether large language models (LLMs) exhibit a similar logarithmic-like structure in their internal numerical representations. By analyzing how numerical values are encoded across different layers of LLMs, we apply dimensionality reduction techniques such as PCA and PLS followed by geometric regression to uncover latent structures in the learned embeddings. Our findings reveal that the model's numerical representations exhibit sublinear spacing, with distances between values aligning with a logarithmic scale. This suggests that LLMs, much like humans, may encode numbers in a compressed, non-uniform manner.