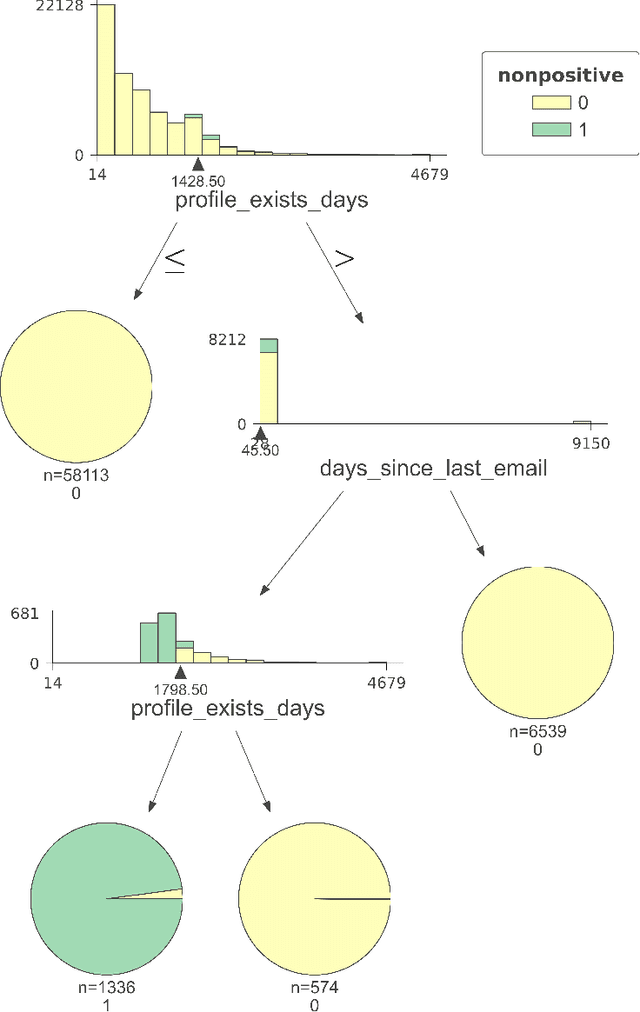
MURAL: An Unsupervised Random Forest-Based Embedding for Electronic Health Record Data

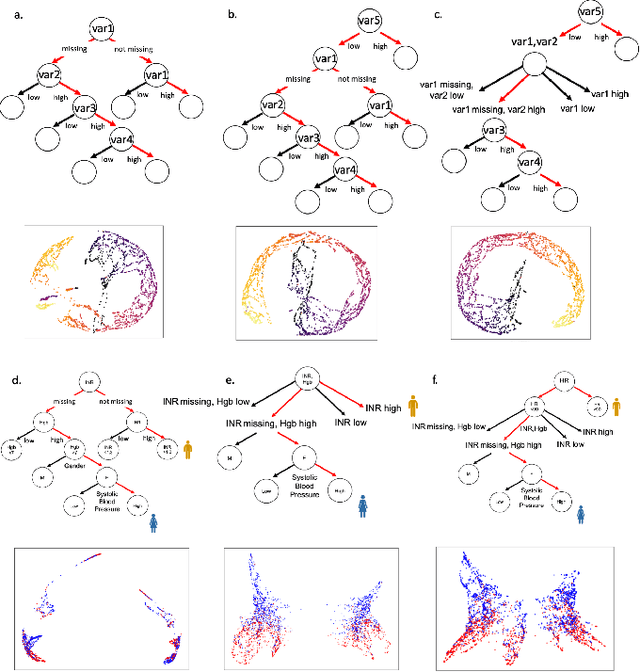
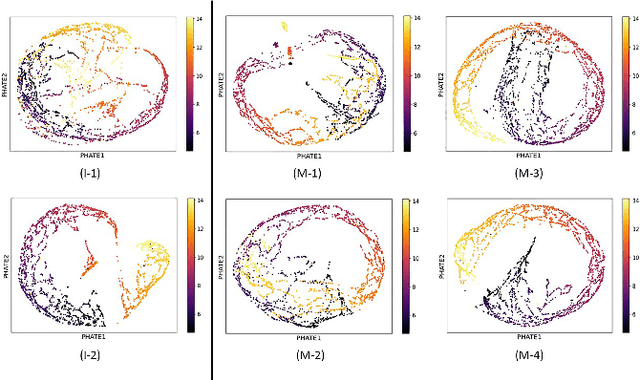
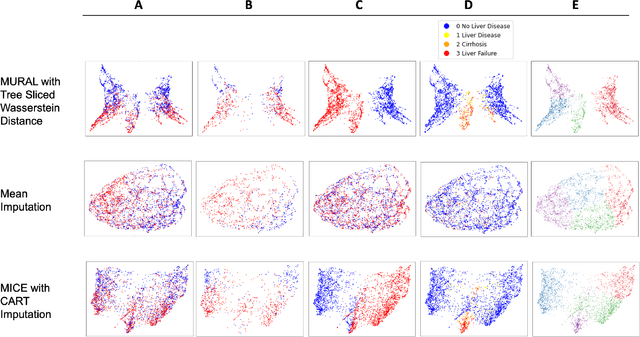
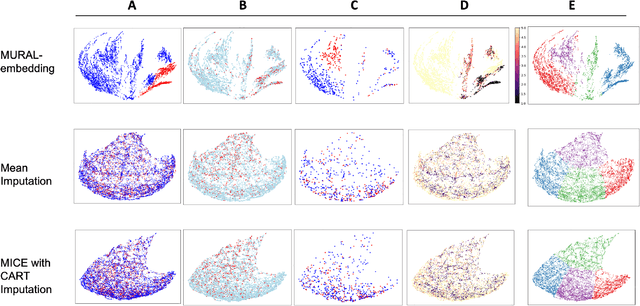
A major challenge in embedding or visualizing clinical patient data is the heterogeneity of variable types including continuous lab values, categorical diagnostic codes, as well as missing or incomplete data. In particular, in EHR data, some variables are {\em missing not at random (MNAR)} but deliberately not collected and thus are a source of information. For example, lab tests may be deemed necessary for some patients on the basis of suspected diagnosis, but not for others. Here we present the MURAL forest -- an unsupervised random forest for representing data with disparate variable types (e.g., categorical, continuous, MNAR). MURAL forests consist of a set of decision trees where node-splitting variables are chosen at random, such that the marginal entropy of all other variables is minimized by the split. This allows us to also split on MNAR variables and discrete variables in a way that is consistent with the continuous variables. The end goal is to learn the MURAL embedding of patients using average tree distances between those patients. These distances can be fed to nonlinear dimensionality reduction method like PHATE to derive visualizable embeddings. While such methods are ubiquitous in continuous-valued datasets (like single cell RNA-sequencing) they have not been used extensively in mixed variable data. We showcase the use of our method on one artificial and two clinical datasets. We show that using our approach, we can visualize and classify data more accurately than competing approaches. Finally, we show that MURAL can also be used to compare cohorts of patients via the recently proposed tree-sliced Wasserstein distances.

Positivity Validation Detection and Explainability via Zero Fraction Multi-Hypothesis Testing and Asymmetrically Pruned Decision Trees

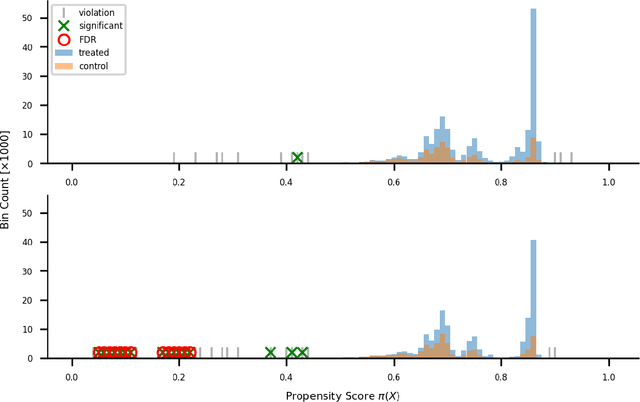
Positivity is one of the three conditions for causal inference from observational data. The standard way to validate positivity is to analyze the distribution of propensity. However, to democratize the ability to do causal inference by non-experts, it is required to design an algorithm to (i) test positivity and (ii) explain where in the covariate space positivity is lacking. The latter could be used to either suggest the limitation of further causal analysis and/or encourage experimentation where positivity is violated. The contribution of this paper is first present the problem of automatic positivity analysis and secondly to propose an algorithm based on a two steps process. The first step, models the propensity condition on the covariates and then analyze the latter distribution using multiple hypothesis testing to create positivity violation labels. The second step uses asymmetrically pruned decision trees for explainability. The latter is further converted into readable text a non-expert can understand. We demonstrate our method on a proprietary data-set of a large software enterprise.

Towards a Taxonomy of Graph Learning Datasets

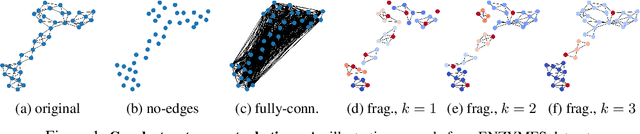
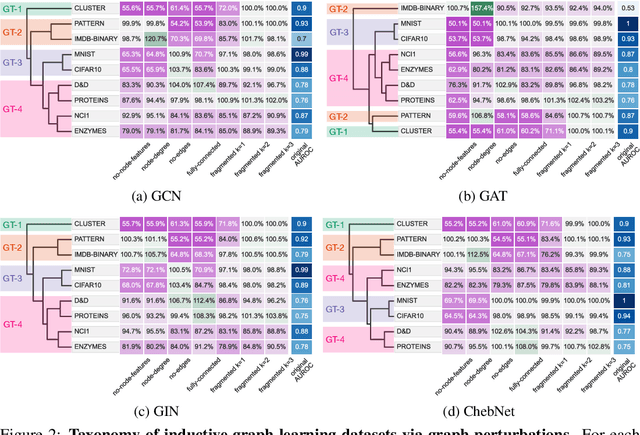
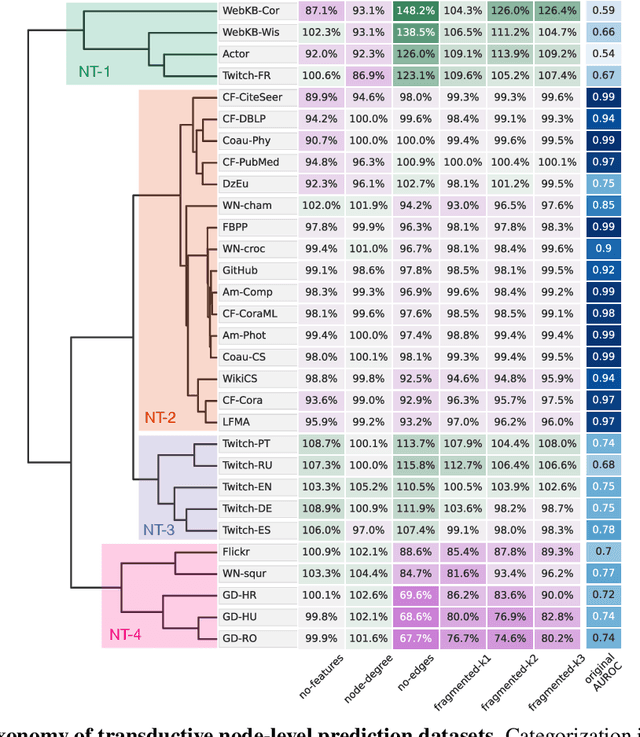
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.

Hierarchical graph neural nets can capture long-range interactions

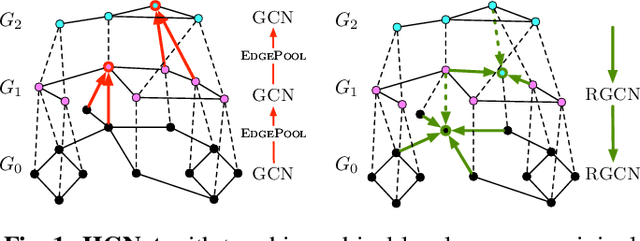
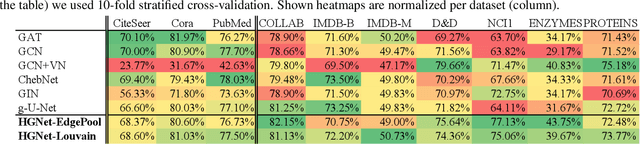
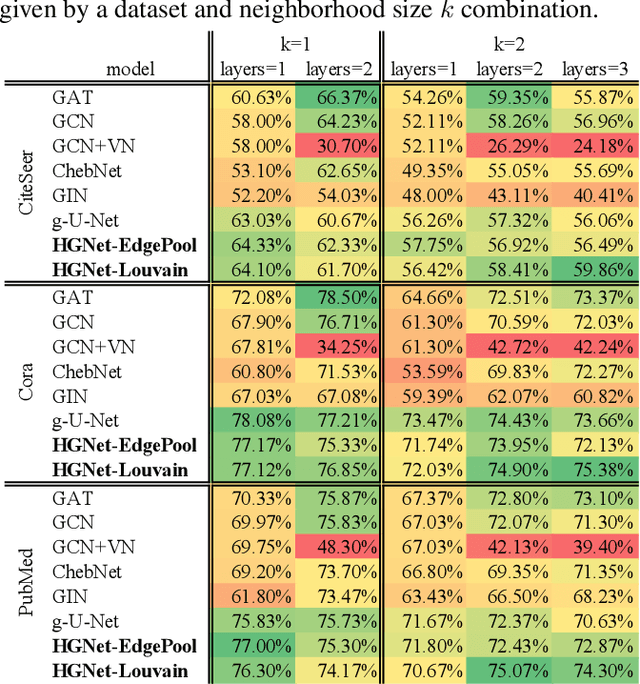
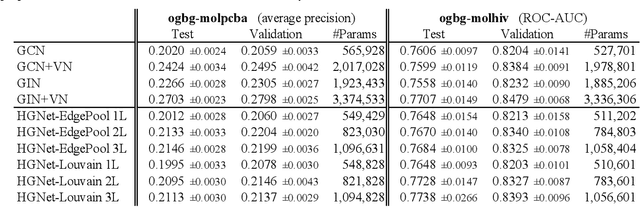
Graph neural networks (GNNs) based on message passing between neighboring nodes are known to be insufficient for capturing long-range interactions in graphs. In this project we study hierarchical message passing models that leverage a multi-resolution representation of a given graph. This facilitates learning of features that span large receptive fields without loss of local information, an aspect not studied in preceding work on hierarchical GNNs. We introduce Hierarchical Graph Net (HGNet), which for any two connected nodes guarantees existence of message-passing paths of at most logarithmic length w.r.t. the input graph size. Yet, under mild assumptions, its internal hierarchy maintains asymptotic size equivalent to that of the input graph. We observe that our HGNet outperforms conventional stacking of GCN layers particularly in molecular property prediction benchmarks. Finally, we propose two benchmarking tasks designed to elucidate capability of GNNs to leverage long-range interactions in graphs.

Embedding Signals on Knowledge Graphs with Unbalanced Diffusion Earth Mover's Distance

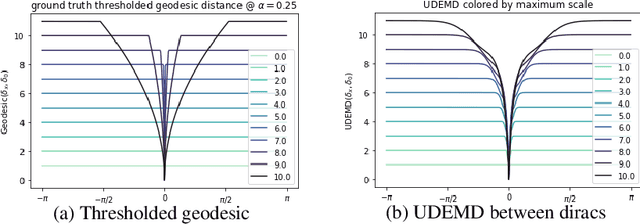
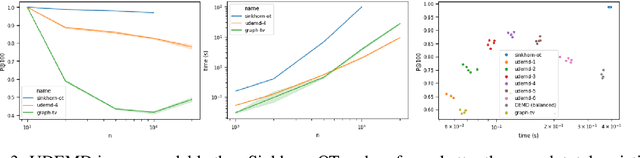
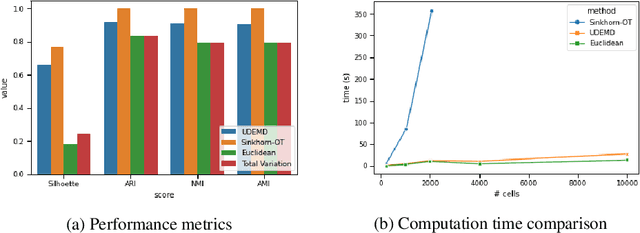
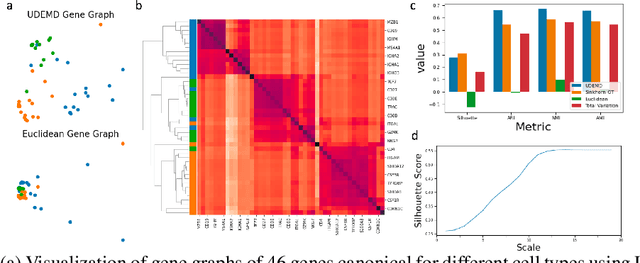
In modern relational machine learning it is common to encounter large graphs that arise via interactions or similarities between observations in many domains. Further, in many cases the target entities for analysis are actually signals on such graphs. We propose to compare and organize such datasets of graph signals by using an earth mover's distance (EMD) with a geodesic cost over the underlying graph. Typically, EMD is computed by optimizing over the cost of transporting one probability distribution to another over an underlying metric space. However, this is inefficient when computing the EMD between many signals. Here, we propose an unbalanced graph earth mover's distance that efficiently embeds the unbalanced EMD on an underlying graph into an $L^1$ space, whose metric we call unbalanced diffusion earth mover's distance (UDEMD). This leads us to an efficient nearest neighbors kernel over many signals defined on a large graph. Next, we show how this gives distances between graph signals that are robust to noise. Finally, we apply this to organizing patients based on clinical notes who are modelled as signals on the SNOMED-CT medical knowledge graph, embedding lymphoblast cells modeled as signals on a gene graph, and organizing genes modeled as signals over a large peripheral blood mononuclear (PBMC) cell graph. In each case, we show that UDEMD-based embeddings find accurate distances that are highly efficient compared to other methods.

Parametric Scattering Networks

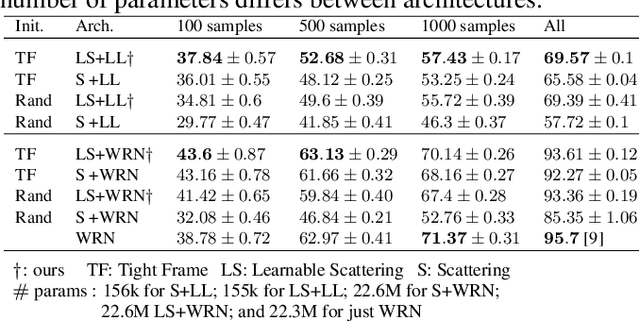
The wavelet scattering transform creates geometric invariants and deformation stability from an initial structured signal. In multiple signal domains it has been shown to yield more discriminative representations compared to other non-learned representations, and to outperform learned representations in certain tasks, particularly on limited labeled data and highly structured signals. The wavelet filters used in the scattering transform are typically selected to create a tight frame via a parameterized mother wavelet. Focusing on Morlet wavelets, we propose to instead adapt the scales, orientations, and slants of the filters to produce problem-specific parametrizations of the scattering transform. We show that our learned versions of the scattering transform yield significant performance gains over the standard scattering transform in the small sample classification settings, and our empirical results suggest that tight frames may not always be necessary for scattering transforms to extract effective representations.

Diffusion Earth Mover's Distance and Distribution Embeddings

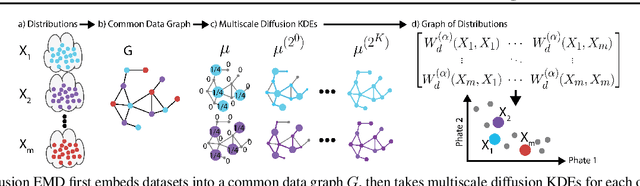
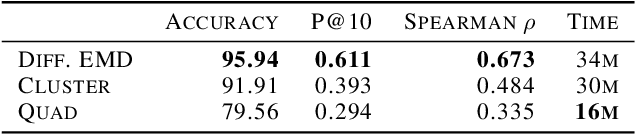
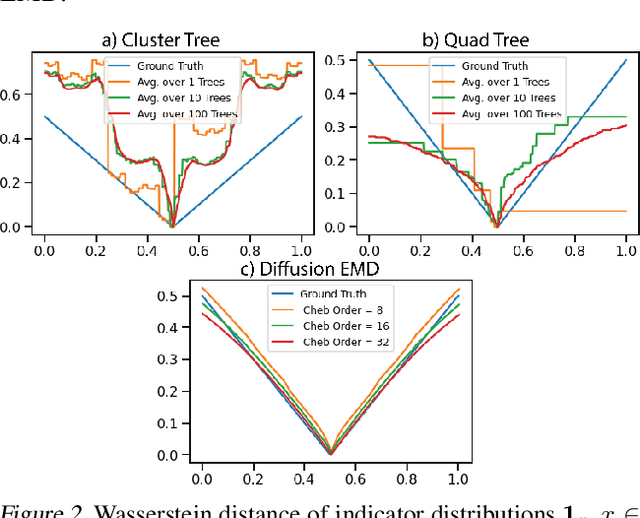
We propose a new fast method of measuring distances between large numbers of related high dimensional datasets called the Diffusion Earth Mover's Distance (EMD). We model the datasets as distributions supported on common data graph that is derived from the affinity matrix computed on the combined data. In such cases where the graph is a discretization of an underlying Riemannian closed manifold, we prove that Diffusion EMD is topologically equivalent to the standard EMD with a geodesic ground distance. Diffusion EMD can be computed in $\tilde{O}(n)$ time and is more accurate than similarly fast algorithms such as tree-based EMDs. We also show Diffusion EMD is fully differentiable, making it amenable to future uses in gradient-descent frameworks such as deep neural networks. Finally, we demonstrate an application of Diffusion EMD to single cell data collected from 210 COVID-19 patient samples at Yale New Haven Hospital. Here, Diffusion EMD can derive distances between patients on the manifold of cells at least two orders of magnitude faster than equally accurate methods. This distance matrix between patients can be embedded into a higher level patient manifold which uncovers structure and heterogeneity in patients. More generally, Diffusion EMD is applicable to all datasets that are massively collected in parallel in many medical and biological systems.

Multimodal data visualization, denoising and clustering with integrated diffusion

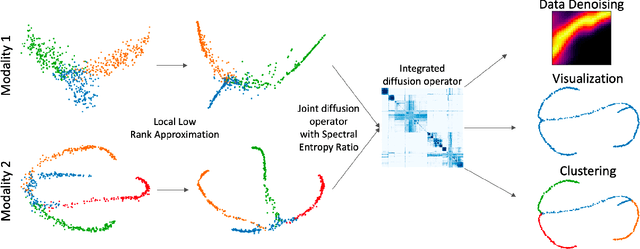
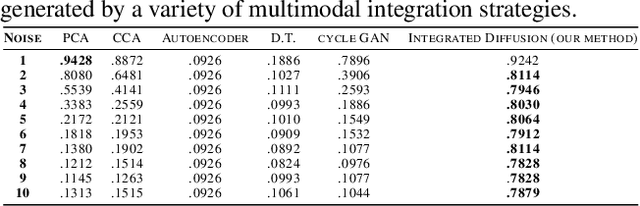
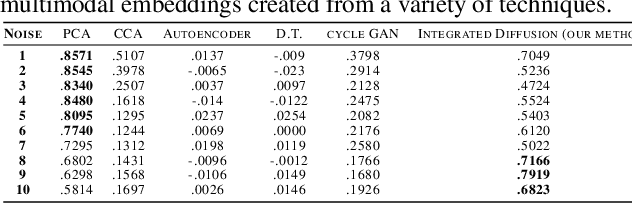
We propose a method called integrated diffusion for combining multimodal datasets, or data gathered via several different measurements on the same system, to create a joint data diffusion operator. As real world data suffers from both local and global noise, we introduce mechanisms to optimally calculate a diffusion operator that reflects the combined information from both modalities. We show the utility of this joint operator in data denoising, visualization and clustering, performing better than other methods to integrate and analyze multimodal data. We apply our method to multi-omic data generated from blood cells, measuring both gene expression and chromatin accessibility. Our approach better visualizes the geometry of the joint data, captures known cross-modality associations and identifies known cellular populations. More generally, integrated diffusion is broadly applicable to multimodal datasets generated in many medical and biological systems.

Visualizing High-Dimensional Trajectories on the Loss-Landscape of ANNs

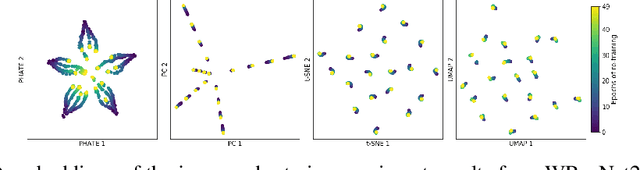
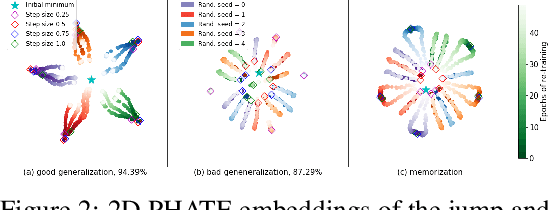
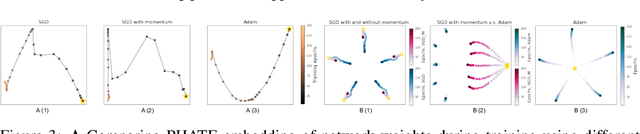
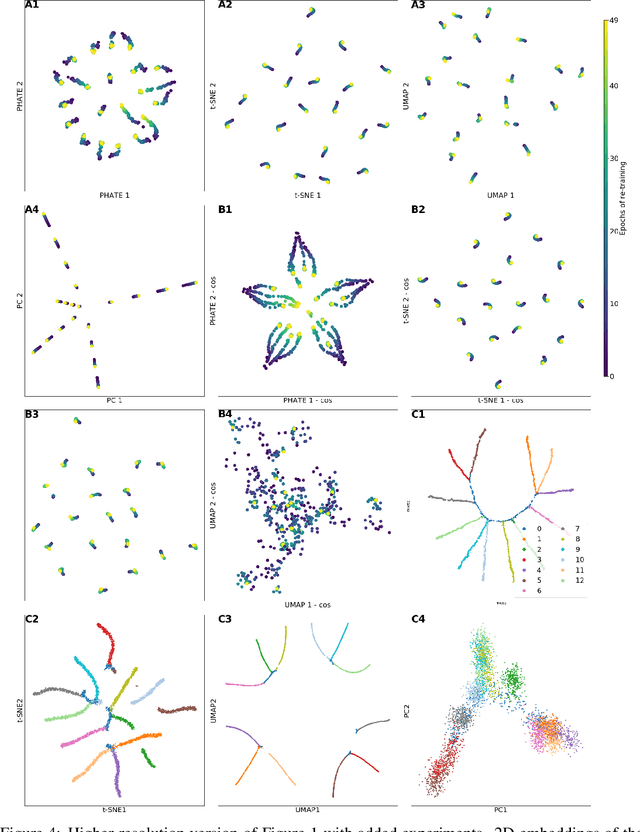
Training artificial neural networks requires the optimization of highly non-convex loss functions. Throughout the years, the scientific community has developed an extensive set of tools and architectures that render this optimization task tractable and a general intuition has been developed for choosing hyper parameters that help the models reach minima that generalize well to unseen data. However, for the most part, the difference in trainability in between architectures, tasks and even the gap in network generalization abilities still remain unexplained. Visualization tools have played a key role in uncovering key geometric characteristics of the loss-landscape of ANNs and how they impact trainability and generalization capabilities. However, most visualizations methods proposed so far have been relatively limited in their capabilities since they are of linear nature and only capture features in a limited number of dimensions. We propose the use of the modern dimensionality reduction method PHATE which represents the SOTA in terms of capturing both global and local structures of high-dimensional data. We apply this method to visualize the loss landscape during and after training. Our visualizations reveal differences in training trajectories and generalization capabilities when used to make comparisons between optimization methods, initializations, architectures, and datasets. Given this success we anticipate this method to be used in making informed choices about these aspects of neural networks.

Geometric Scattering Attention Networks

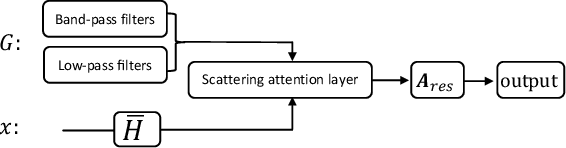
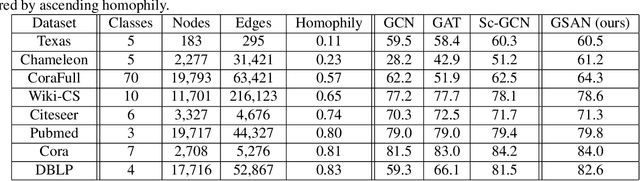
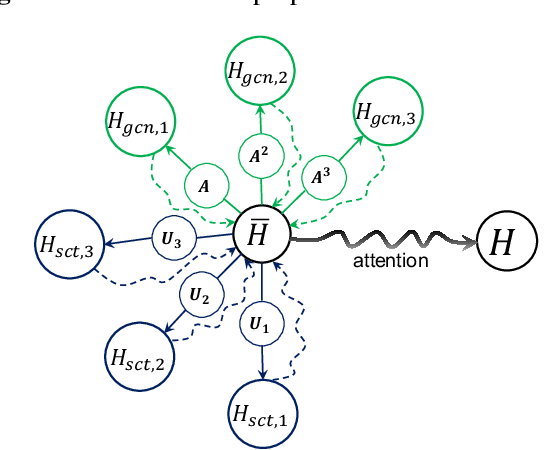
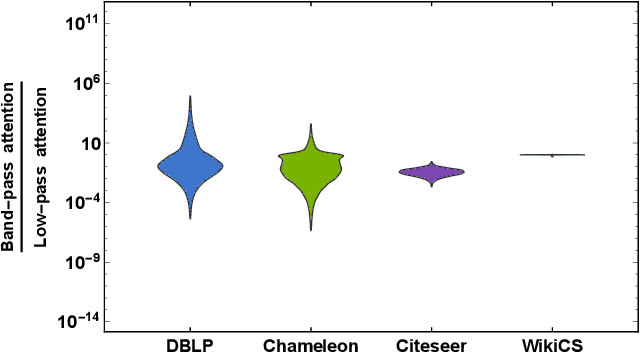
Geometric scattering has recently gained recognition in graph representation learning, and recent work has shown that integrating scattering features in graph convolution networks (GCNs) can alleviate the typical oversmoothing of features in node representation learning. However, scattering methods often rely on handcrafted design, requiring careful selection of frequency bands via a cascade of wavelet transforms, as well as an effective weight sharing scheme to combine together low- and band-pass information. Here, we introduce a new attention-based architecture to produce adaptive task-driven node representations by implicitly learning node-wise weights for combining multiple scattering and GCN channels in the network. We show the resulting geometric scattering attention network (GSAN) outperforms previous networks in semi-supervised node classification, while also enabling a spectral study of extracted information by examining node-wise attention weights.