Guang Cheng
Purdue
Variance Reduction on Adaptive Stochastic Mirror Descent
Dec 26, 2020
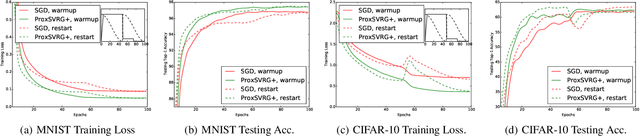
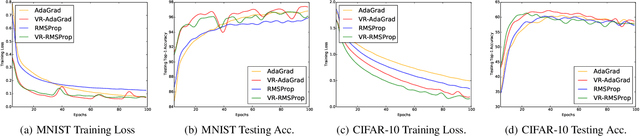
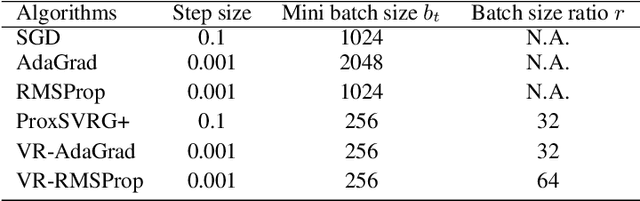
Abstract:We study the idea of variance reduction applied to adaptive stochastic mirror descent algorithms in nonsmooth nonconvex finite-sum optimization problems. We propose a simple yet generalized adaptive mirror descent algorithm with variance reduction named SVRAMD and provide its convergence analysis in different settings. We prove that variance reduction reduces the gradient complexity of most adaptive mirror descent algorithms and boost their convergence. In particular, our general theory implies variance reduction can be applied to algorithms using time-varying step sizes and self-adaptive algorithms such as AdaGrad and RMSProp. Moreover, our convergence rates recover the best existing rates of non-adaptive algorithms. We check the validity of our claims using experiments in deep learning.
Union-net: A deep neural network model adapted to small data sets
Dec 24, 2020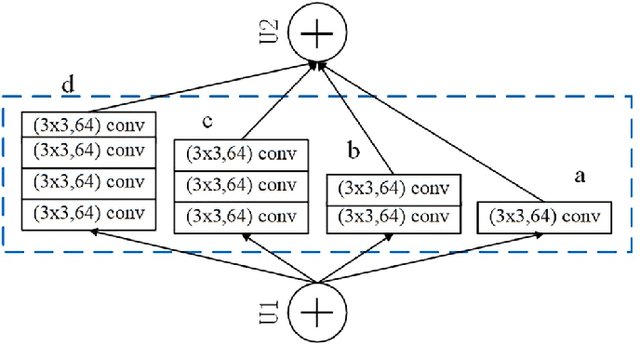
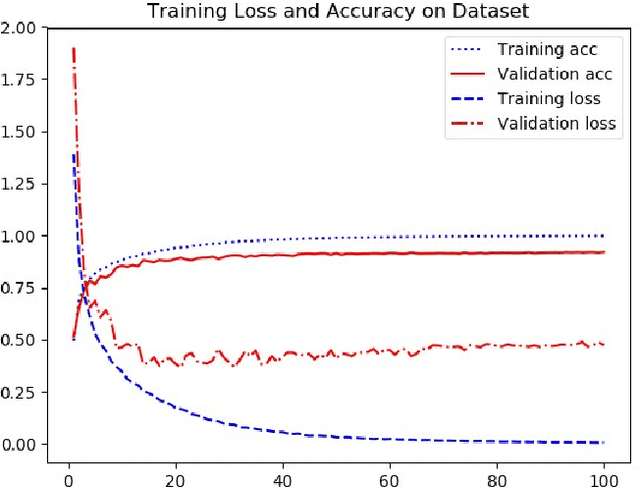
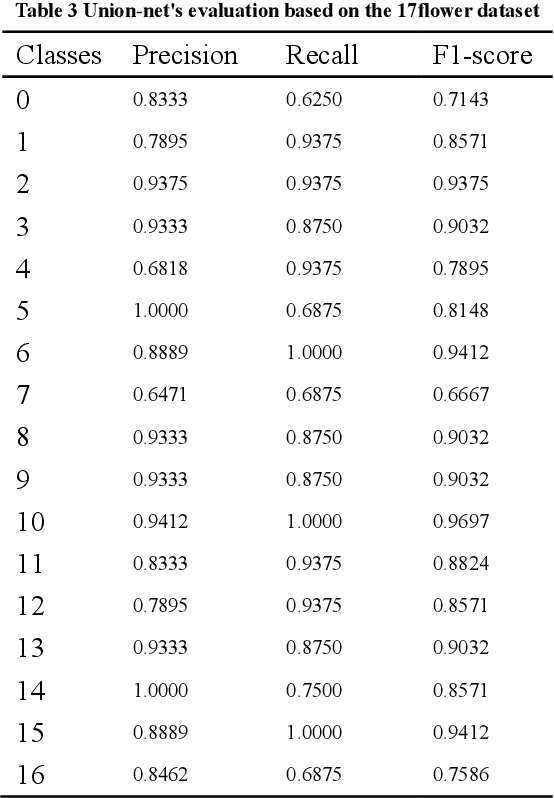
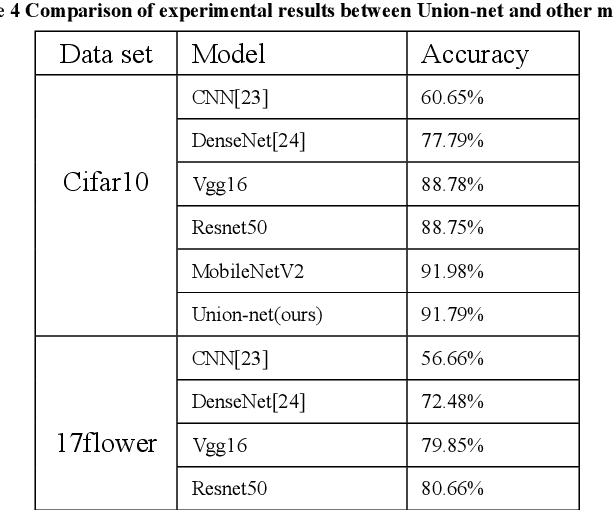
Abstract:In real applications, generally small data sets can be obtained. At present, most of the practical applications of machine learning use classic models based on big data to solve the problem of small data sets. However, the deep neural network model has complex structure, huge model parameters, and training requires more advanced equipment, which brings certain difficulties to the application. Therefore, this paper proposes the concept of union convolution, designing a light deep network model union-net with a shallow network structure and adapting to small data sets. This model combines convolutional network units with different combinations of the same input to form a union module. Each union module is equivalent to a convolutional layer. The serial input and output between the 3 modules constitute a "3-layer" neural network. The output of each union module is fused and added as the input of the last convolutional layer to form a complex network with a 4-layer network structure. It solves the problem that the deep network model network is too deep and the transmission path is too long, which causes the loss of the underlying information transmission. Because the model has fewer model parameters and fewer channels, it can better adapt to small data sets. It solves the problem that the deep network model is prone to overfitting in training small data sets. Use the public data sets cifar10 and 17flowers to conduct multi-classification experiments. Experiments show that the Union-net model can perform well in classification of large data sets and small data sets. It has high practical value in daily application scenarios. The model code is published at https://github.com/yeaso/union-net
Adversarially Robust Estimate and Risk Analysis in Linear Regression
Dec 18, 2020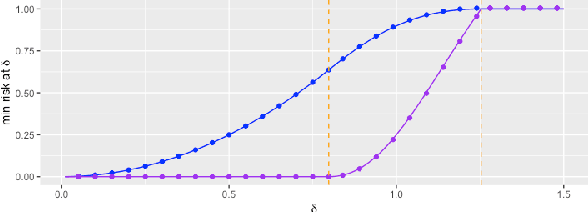

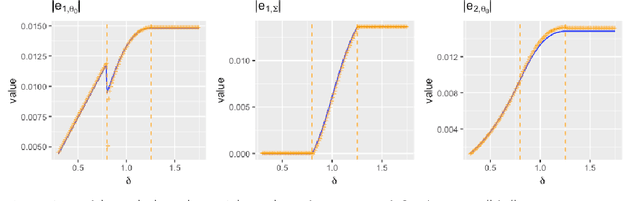
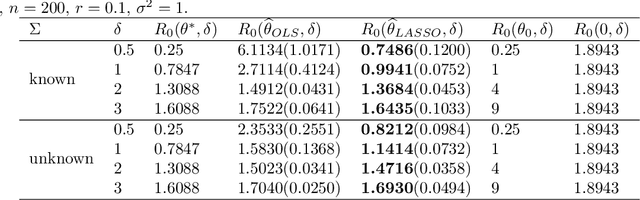
Abstract:Adversarially robust learning aims to design algorithms that are robust to small adversarial perturbations on input variables. Beyond the existing studies on the predictive performance to adversarial samples, our goal is to understand statistical properties of adversarially robust estimates and analyze adversarial risk in the setup of linear regression models. By discovering the statistical minimax rate of convergence of adversarially robust estimators, we emphasize the importance of incorporating model information, e.g., sparsity, in adversarially robust learning. Further, we reveal an explicit connection of adversarial and standard estimates, and propose a straightforward two-stage adversarial learning framework, which facilitates to utilize model structure information to improve adversarial robustness. In theory, the consistency of the adversarially robust estimator is proven and its Bahadur representation is also developed for the statistical inference purpose. The proposed estimator converges in a sharp rate under either low-dimensional or sparse scenario. Moreover, our theory confirms two phenomena in adversarially robust learning: adversarial robustness hurts generalization, and unlabeled data help improve the generalization. In the end, we conduct numerical simulations to verify our theory.
Online Forgetting Process for Linear Regression Models
Dec 03, 2020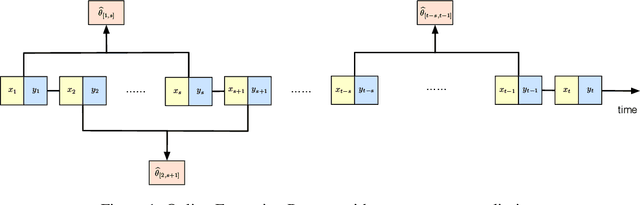
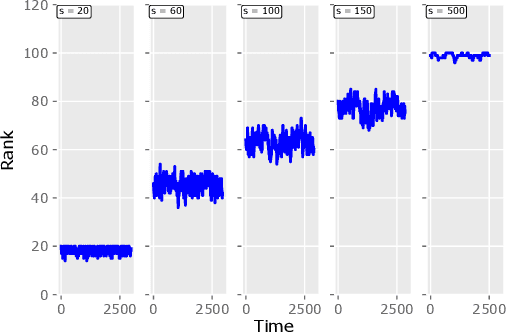
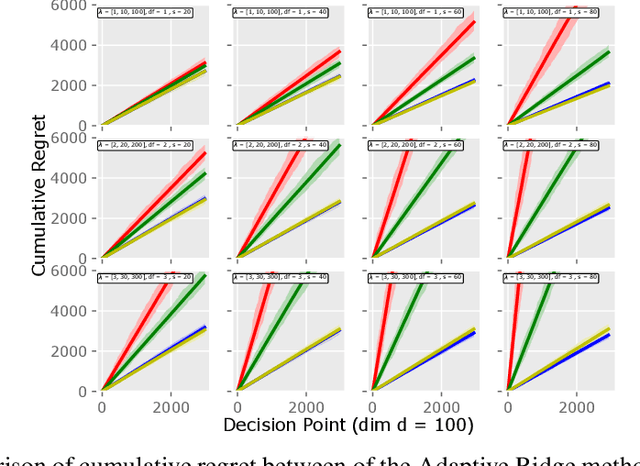
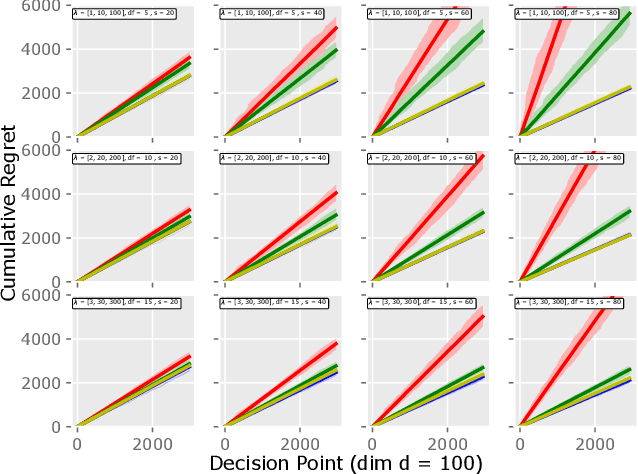
Abstract:Motivated by the EU's "Right To Be Forgotten" regulation, we initiate a study of statistical data deletion problems where users' data are accessible only for a limited period of time. This setting is formulated as an online supervised learning task with \textit{constant memory limit}. We propose a deletion-aware algorithm \texttt{FIFD-OLS} for the low dimensional case, and witness a catastrophic rank swinging phenomenon due to the data deletion operation, which leads to statistical inefficiency. As a remedy, we propose the \texttt{FIFD-Adaptive Ridge} algorithm with a novel online regularization scheme, that effectively offsets the uncertainty from deletion. In theory, we provide the cumulative regret upper bound for both online forgetting algorithms. In the experiment, we showed \texttt{FIFD-Adaptive Ridge} outperforms the ridge regression algorithm with fixed regularization level, and hopefully sheds some light on more complex statistical models.
Efficient Variational Inference for Sparse Deep Learning with Theoretical Guarantee
Nov 15, 2020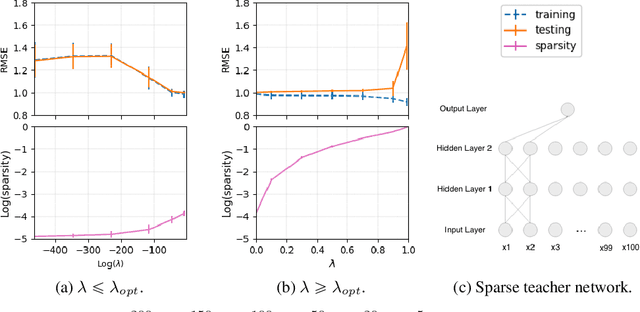
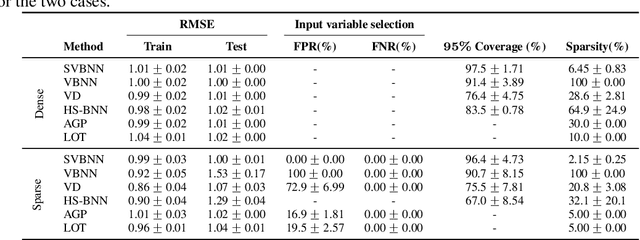
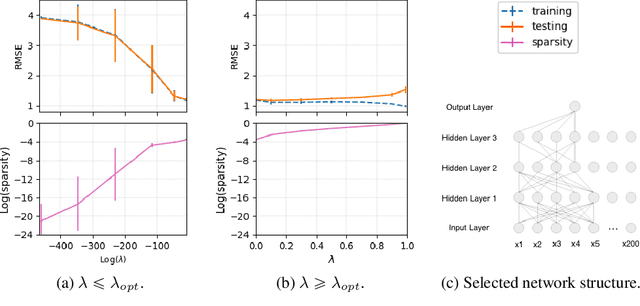
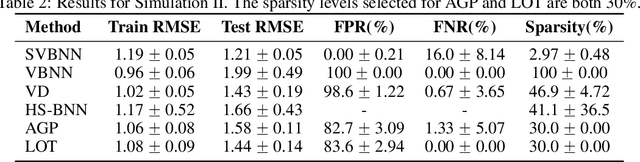
Abstract:Sparse deep learning aims to address the challenge of huge storage consumption by deep neural networks, and to recover the sparse structure of target functions. Although tremendous empirical successes have been achieved, most sparse deep learning algorithms are lacking of theoretical support. On the other hand, another line of works have proposed theoretical frameworks that are computationally infeasible. In this paper, we train sparse deep neural networks with a fully Bayesian treatment under spike-and-slab priors, and develop a set of computationally efficient variational inferences via continuous relaxation of Bernoulli distribution. The variational posterior contraction rate is provided, which justifies the consistency of the proposed variational Bayes method. Notably, our empirical results demonstrate that this variational procedure provides uncertainty quantification in terms of Bayesian predictive distribution and is also capable to accomplish consistent variable selection by training a sparse multi-layer neural network.
Nearly Optimal Variational Inference for High Dimensional Regression with Shrinkage Priors
Oct 24, 2020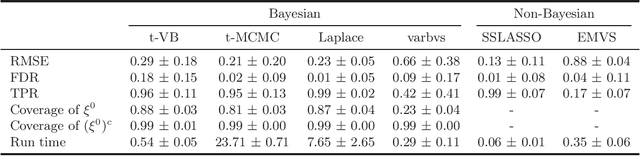
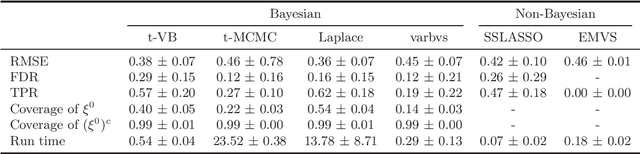
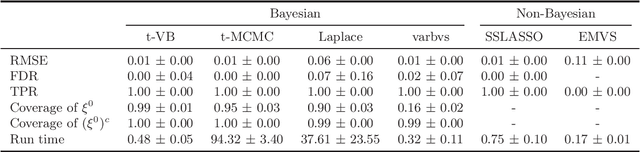
Abstract:We propose a variational Bayesian (VB) procedure for high-dimensional linear model inferences with heavy tail shrinkage priors, such as student-t prior. Theoretically, we establish the consistency of the proposed VB method and prove that under the proper choice of prior specifications, the contraction rate of the VB posterior is nearly optimal. It justifies the validity of VB inference as an alternative of Markov Chain Monte Carlo (MCMC) sampling. Meanwhile, comparing to conventional MCMC methods, the VB procedure achieves much higher computational efficiency, which greatly alleviates the computing burden for modern machine learning applications such as massive data analysis. Through numerical studies, we demonstrate that the proposed VB method leads to shorter computing time, higher estimation accuracy, and lower variable selection error than competitive sparse Bayesian methods.
On the Generalization Properties of Adversarial Training
Aug 15, 2020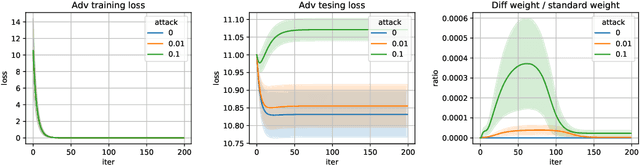

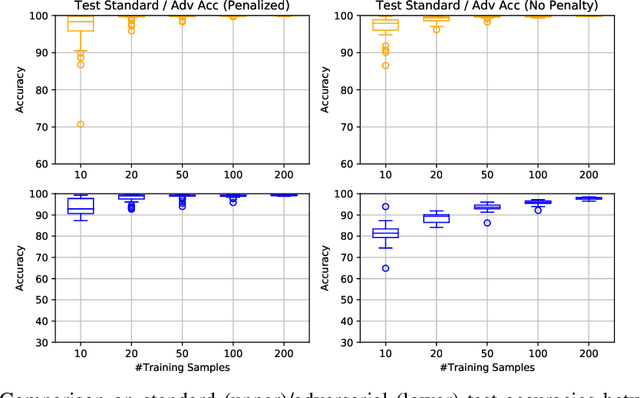
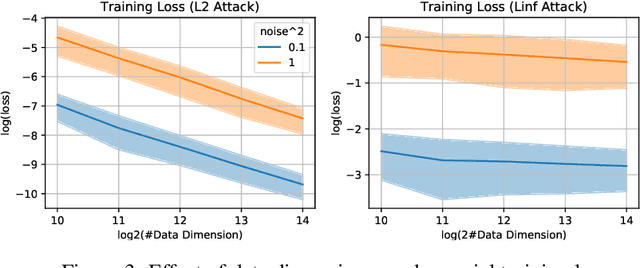
Abstract:Modern machine learning and deep learning models are shown to be vulnerable when testing data are slightly perturbed. Theoretical studies of adversarial training algorithms mostly focus on their adversarial training losses or local convergence properties. In contrast, this paper studies the generalization performance of a generic adversarial training algorithm. Specifically, we consider linear regression models and two-layer neural networks (with lazy training) using squared loss under both low-dimensional and high-dimensional regimes. In the former regime, the adversarial risk of the trained models will converge to the minimal adversarial risk. In the latter regime, we discover that data interpolation prevents the adversarial robust estimator from being consistent (i.e. converge in probability). Therefore, inspired by successes of the least absolute shrinkage and selection operator (LASSO), we incorporate the L1 penalty in the high dimensional adversarial learning, and show that it leads to consistent adversarial robust estimation in both theory and numerical trials.
Regularization Matters: A Nonparametric Perspective on Overparametrized Neural Network
Jul 06, 2020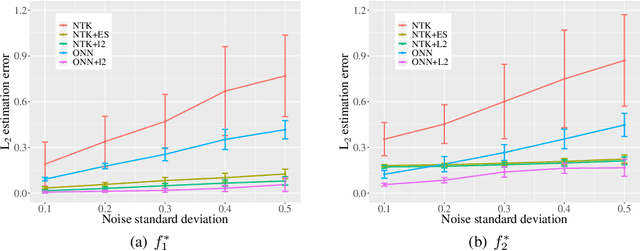
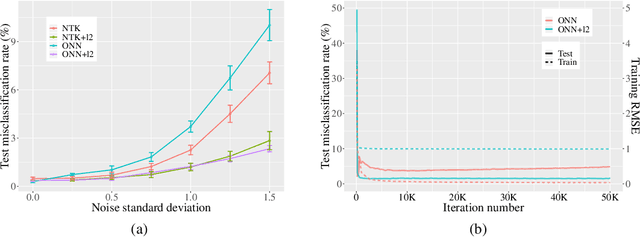
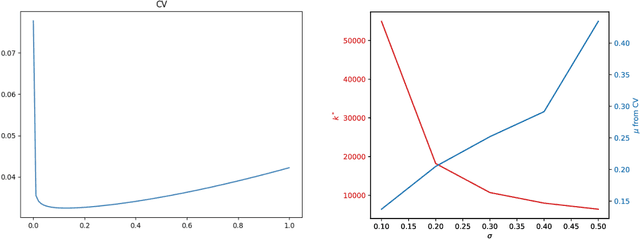
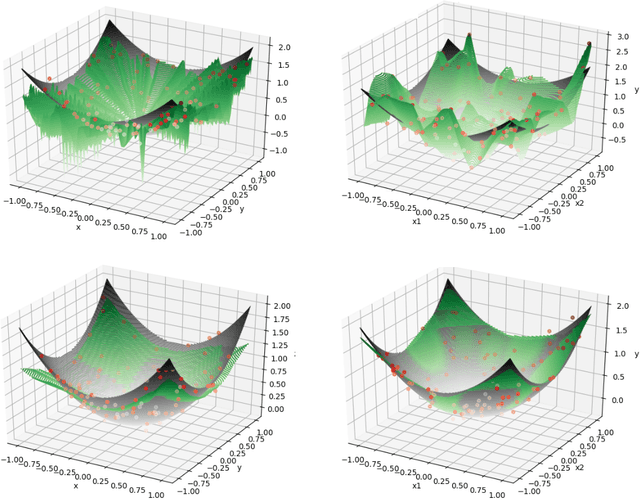
Abstract:Overparametrized neural networks trained by gradient descent (GD) can provably overfit any training data. However, the generalization guarantee may not hold for noisy data. From a nonparametric perspective, this paper studies how well overparametrized neural networks can recover the true target function in the presence of random noises. We establish a lower bound on the $L_2$ estimation error with respect to the GD iteration, which is away from zero without a delicate choice of early stopping. In turn, through a comprehensive analysis of $\ell_2$-regularized GD trajectories, we prove that for overparametrized one-hidden-layer ReLU neural network with the $\ell_2$ regularization: (1) the output is close to that of the kernel ridge regression with the corresponding neural tangent kernel; (2) minimax {optimal} rate of $L_2$ estimation error is achieved. Numerical experiments confirm our theory and further demonstrate that the $\ell_2$ regularization approach improves the training robustness and works for a wider range of neural networks.
Online Regularization for High-Dimensional Dynamic Pricing Algorithms
Jul 05, 2020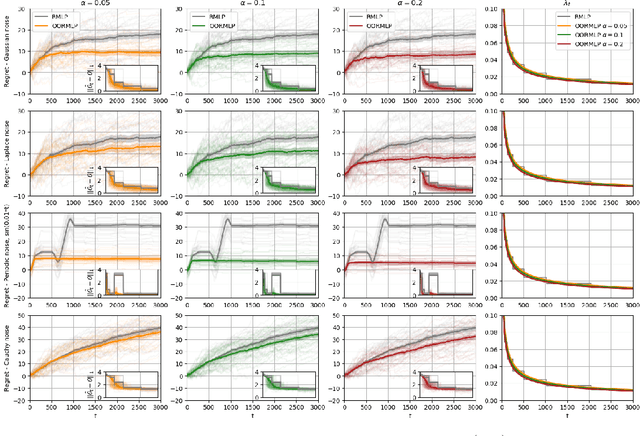
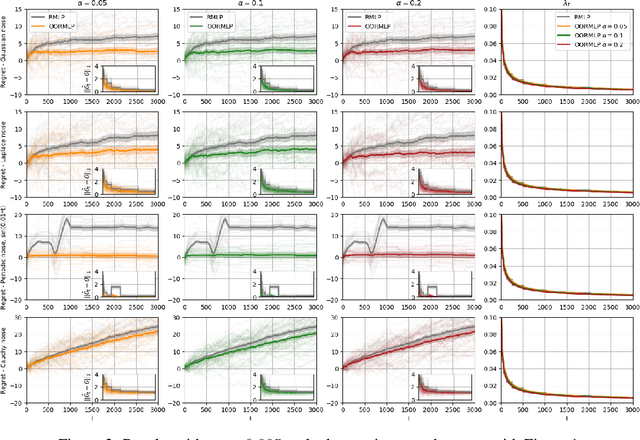
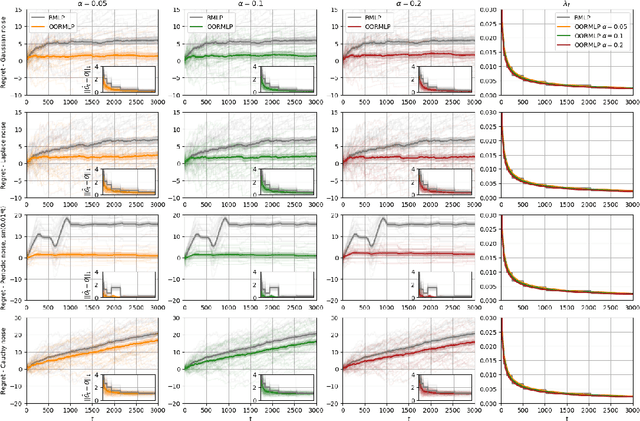
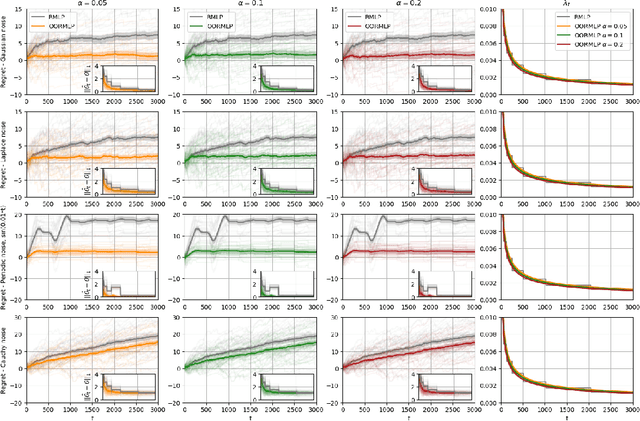
Abstract:We propose a novel \textit{online regularization} scheme for revenue-maximization in high-dimensional dynamic pricing algorithms. The online regularization scheme equips the proposed optimistic online regularized maximum likelihood pricing (\texttt{OORMLP}) algorithm with three major advantages: encode market noise knowledge into pricing process optimism; empower online statistical learning with always-validity over all decision points; envelop prediction error process with time-uniform non-asymptotic oracle inequalities. This type of non-asymptotic inference results allows us to design safer and more robust dynamic pricing algorithms in practice. In theory, the proposed \texttt{OORMLP} algorithm exploits the sparsity structure of high-dimensional models and obtains a logarithmic regret in a decision horizon. These theoretical advances are made possible by proposing an optimistic online LASSO procedure that resolves dynamic pricing problems at the \textit{process} level, based on a novel use of non-asymptotic martingale concentration. In experiments, we evaluate \texttt{OORMLP} in different synthetic pricing problem settings and observe that \texttt{OORMLP} performs better than \texttt{RMLP} proposed in \cite{javanmard2019dynamic}.
Directional Pruning of Deep Neural Networks
Jun 16, 2020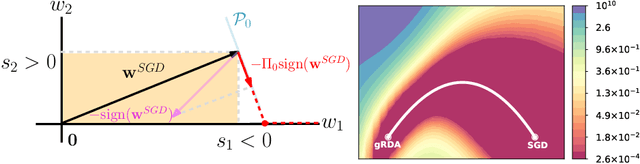
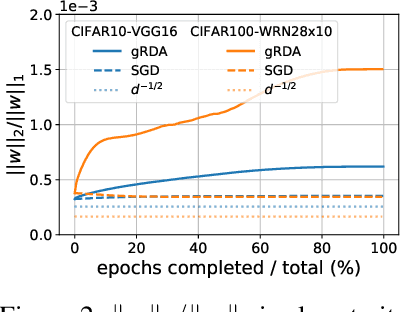
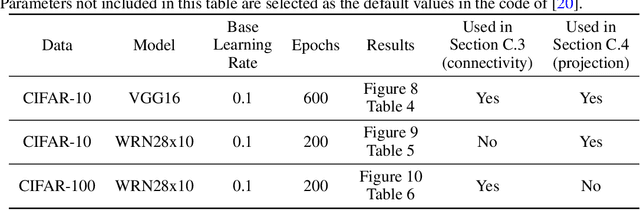
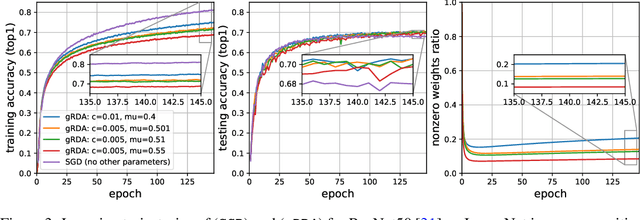
Abstract:In the light of the fact that the stochastic gradient descent (SGD) often finds a flat minimum valley in the training loss, we propose a novel directional pruning method which searches for a sparse minimizer in that flat region. The proposed pruning method is automatic in the sense that neither retraining nor expert knowledge is required. To overcome the computational formidability of estimating the flat directions, we propose to use a carefully tuned $\ell_1$ proximal gradient algorithm which can provably achieve the directional pruning with a small learning rate after sufficient training. The empirical results show that our algorithm performs competitively in highly sparse regime (92\% sparsity) among many existing automatic pruning methods on the ResNet50 with the ImageNet, while using only a slightly higher wall time and memory footprint than the SGD. Using the VGG16 and the wide ResNet 28x10 on the CIFAR-10 and CIFAR-100, we demonstrate that our algorithm reaches the same minima valley as the SGD, and the minima found by our algorithm and the SGD do not deviate in directions that impact the training loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge