Distributed Bootstrap for Simultaneous Inference Under High Dimensionality

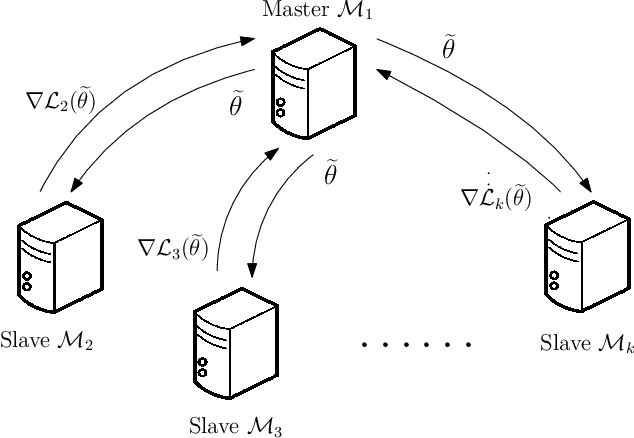
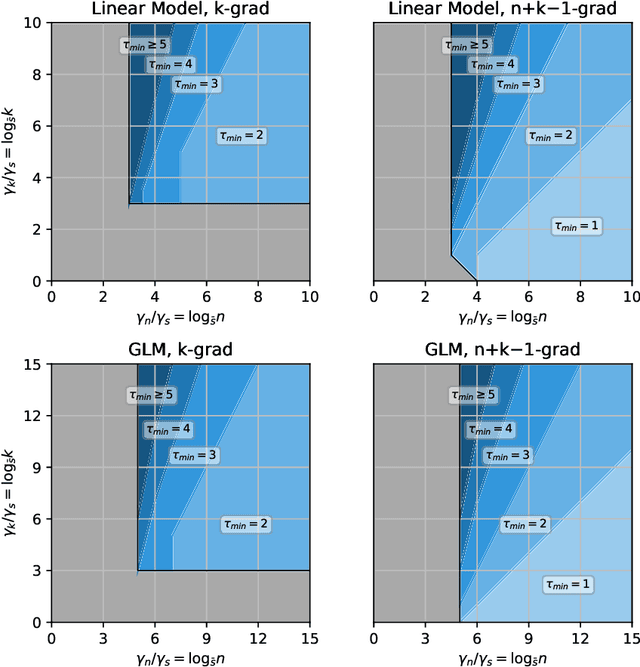
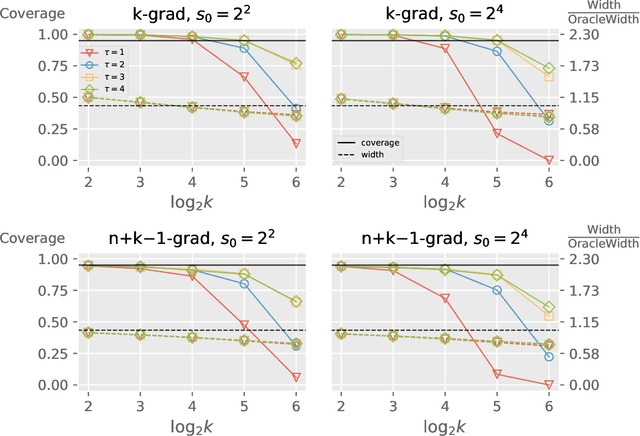
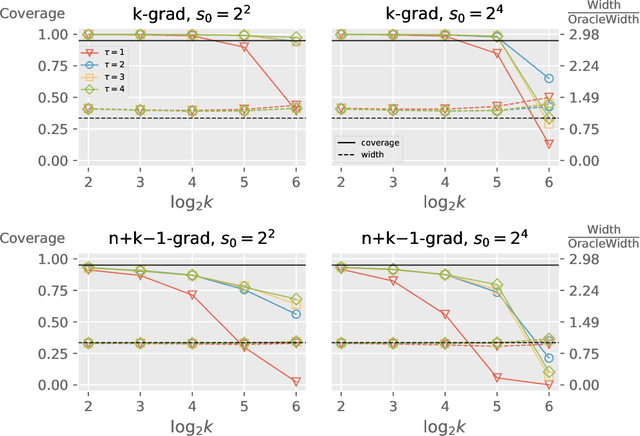
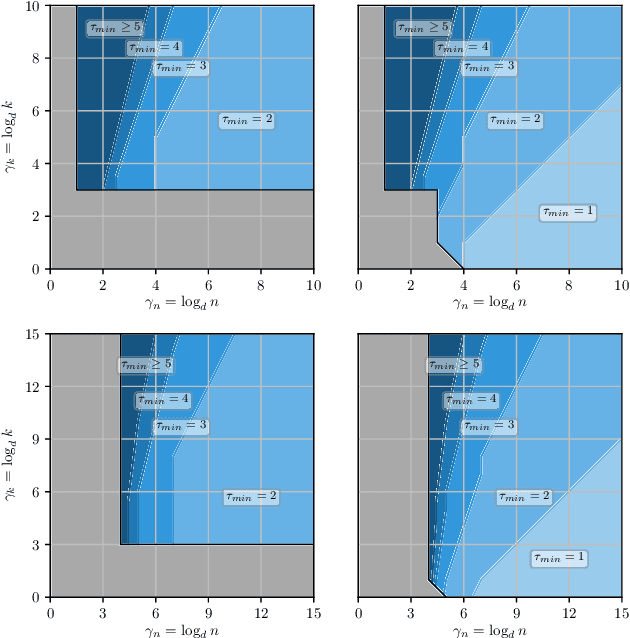
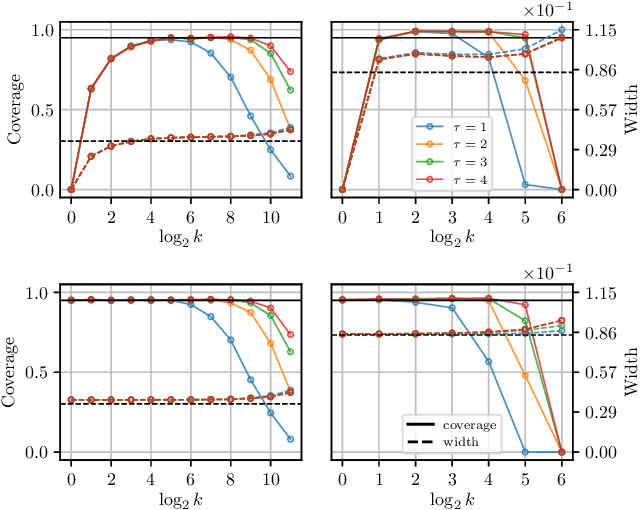
We propose a distributed bootstrap method for simultaneous inference on high-dimensional massive data that are stored and processed with many machines. The method produces a $\ell_\infty$-norm confidence region based on a communication-efficient de-biased lasso, and we propose an efficient cross-validation approach to tune the method at every iteration. We theoretically prove a lower bound on the number of communication rounds $\tau_{\min}$ that warrants the statistical accuracy and efficiency. Furthermore, $\tau_{\min}$ only increases logarithmically with the number of workers and intrinsic dimensionality, while nearly invariant to the nominal dimensionality. We test our theory by extensive simulation studies, and a variable screening task on a semi-synthetic dataset based on the US Airline On-time Performance dataset. The code to reproduce the numerical results is available at GitHub: https://github.com/skchao74/Distributed-bootstrap.

Directional Pruning of Deep Neural Networks

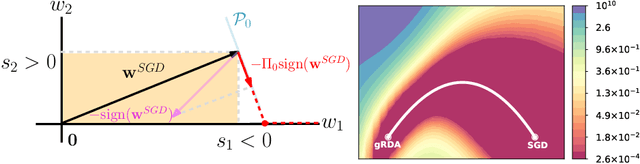
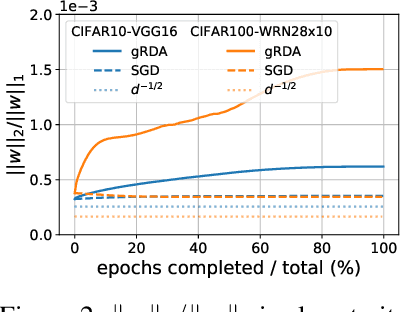
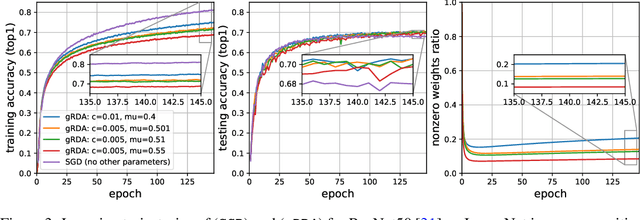
In the light of the fact that the stochastic gradient descent (SGD) often finds a flat minimum valley in the training loss, we propose a novel directional pruning method which searches for a sparse minimizer in that flat region. The proposed pruning method is automatic in the sense that neither retraining nor expert knowledge is required. To overcome the computational formidability of estimating the flat directions, we propose to use a carefully tuned $\ell_1$ proximal gradient algorithm which can provably achieve the directional pruning with a small learning rate after sufficient training. The empirical results show that our algorithm performs competitively in highly sparse regime (92\% sparsity) among many existing automatic pruning methods on the ResNet50 with the ImageNet, while using only a slightly higher wall time and memory footprint than the SGD. Using the VGG16 and the wide ResNet 28x10 on the CIFAR-10 and CIFAR-100, we demonstrate that our algorithm reaches the same minima valley as the SGD, and the minima found by our algorithm and the SGD do not deviate in directions that impact the training loss.

Simultaneous Inference for Massive Data: Distributed Bootstrap

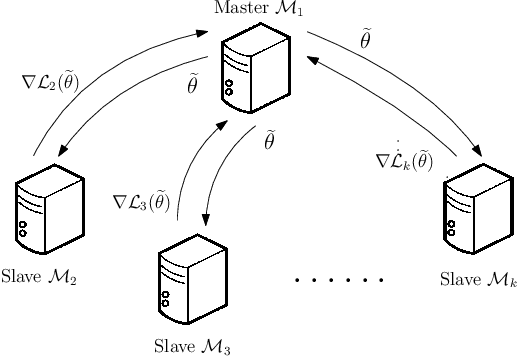
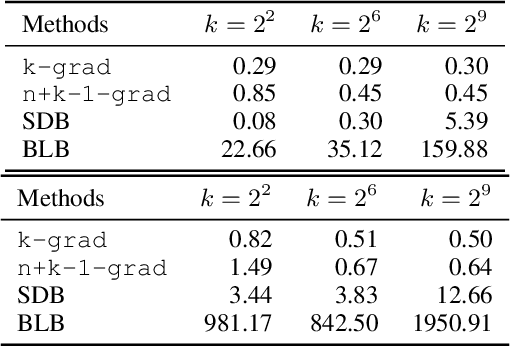
In this paper, we propose a bootstrap method applied to massive data processed distributedly in a large number of machines. This new method is computationally efficient in that we bootstrap on the master machine without over-resampling, typically required by existing methods \cite{kleiner2014scalable,sengupta2016subsampled}, while provably achieving optimal statistical efficiency with minimal communication. Our method does not require repeatedly re-fitting the model but only applies multiplier bootstrap in the master machine on the gradients received from the worker machines. Simulations validate our theory.

A generalization of regularized dual averaging and its dynamics

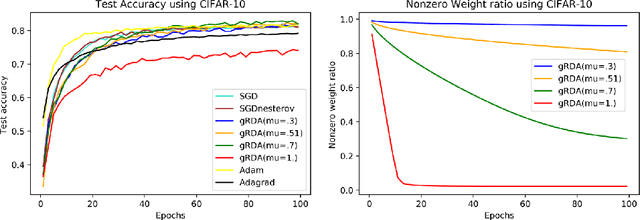
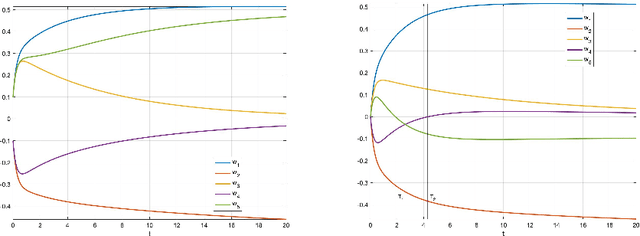
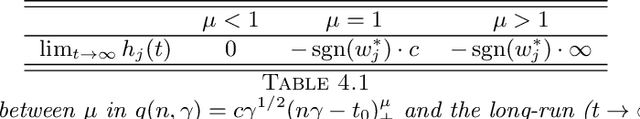
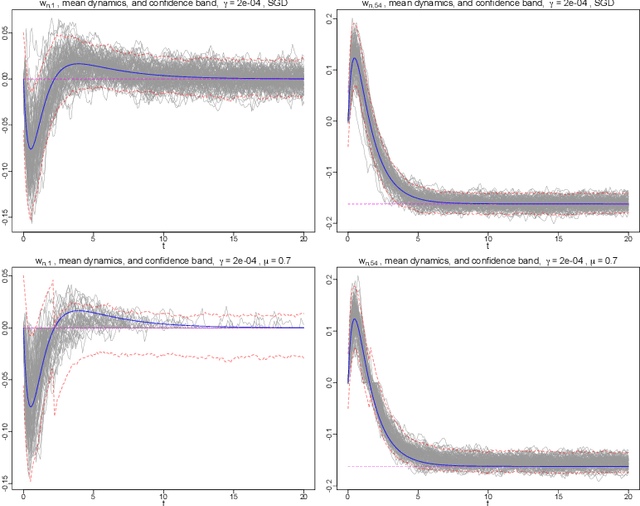
Excessive computational cost for learning large data and streaming data can be alleviated by using stochastic algorithms, such as stochastic gradient descent and its variants. Recent advances improve stochastic algorithms on convergence speed, adaptivity and structural awareness. However, distributional aspects of these new algorithms are poorly understood, especially for structured parameters. To develop statistical inference in this case, we propose a class of generalized regularized dual averaging (gRDA) algorithms with constant step size, which improves RDA (Xiao, 2010; Flammarion and Bach, 2017). Weak convergence of gRDA trajectories are studied, and as a consequence, for the first time in the literature, the asymptotic distributions for online l1 penalized problems become available. These general results apply to both convex and non-convex differentiable loss functions, and in particular, recover the existing regret bound for convex losses (Nemirovski et al., 2009). As important applications, statistical inferential theory on online sparse linear regression and online sparse principal component analysis are developed, and are supported by extensive numerical analysis. Interestingly, when gRDA is properly tuned, support recovery and central limiting distribution (with mean zero) hold simultaneously in the online setting, which is in contrast with the biased central limiting distribution of batch Lasso (Knight and Fu, 2000). Technical devices, including weak convergence of stochastic mirror descent, are developed as by-products with independent interest. Preliminary empirical analysis of modern image data shows that learning very sparse deep neural networks by gRDA does not necessarily sacrifice testing accuracy.