MissDiff: Training Diffusion Models on Tabular Data with Missing Values

The diffusion model has shown remarkable performance in modeling data distributions and synthesizing data. However, the vanilla diffusion model requires complete or fully observed data for training. Incomplete data is a common issue in various real-world applications, including healthcare and finance, particularly when dealing with tabular datasets. This work presents a unified and principled diffusion-based framework for learning from data with missing values under various missing mechanisms. We first observe that the widely adopted "impute-then-generate" pipeline may lead to a biased learning objective. Then we propose to mask the regression loss of Denoising Score Matching in the training phase. We prove the proposed method is consistent in learning the score of data distributions, and the proposed training objective serves as an upper bound for the negative likelihood in certain cases. The proposed framework is evaluated on multiple tabular datasets using realistic and efficacious metrics and is demonstrated to outperform state-of-the-art diffusion model on tabular data with "impute-then-generate" pipeline by a large margin.

Utility Theory of Synthetic Data Generation

Evaluating the utility of synthetic data is critical for measuring the effectiveness and efficiency of synthetic algorithms. Existing results focus on empirical evaluations of the utility of synthetic data, whereas the theoretical understanding of how utility is affected by synthetic data algorithms remains largely unexplored. This paper establishes utility theory from a statistical perspective, aiming to quantitatively assess the utility of synthetic algorithms based on a general metric. The metric is defined as the absolute difference in generalization between models trained on synthetic and original datasets. We establish analytical bounds for this utility metric to investigate critical conditions for the metric to converge. An intriguing result is that the synthetic feature distribution is not necessarily identical to the original one for the convergence of the utility metric as long as the model specification in downstream learning tasks is correct. Another important utility metric is model comparison based on synthetic data. Specifically, we establish sufficient conditions for synthetic data algorithms so that the ranking of generalization performances of models trained on the synthetic data is consistent with that from the original data. Finally, we conduct extensive experiments using non-parametric models and deep neural networks to validate our theoretical findings.

Tight Non-asymptotic Inference via Sub-Gaussian Intrinsic Moment Norm

In non-asymptotic statistical inferences, variance-type parameters of sub-Gaussian distributions play a crucial role. However, direct estimation of these parameters based on the empirical moment generating function (MGF) is infeasible. To this end, we recommend using a sub-Gaussian intrinsic moment norm [Buldygin and Kozachenko (2000), Theorem 1.3] through maximizing a series of normalized moments. Importantly, the recommended norm can not only recover the exponential moment bounds for the corresponding MGFs, but also lead to tighter Hoeffding's sub-Gaussian concentration inequalities. In practice, {\color{black} we propose an intuitive way of checking sub-Gaussian data with a finite sample size by the sub-Gaussian plot}. Intrinsic moment norm can be robustly estimated via a simple plug-in approach. Our theoretical results are applied to non-asymptotic analysis, including the multi-armed bandit.

Statistical Theory of Differentially Private Marginal-based Data Synthesis Algorithms

Marginal-based methods achieve promising performance in the synthetic data competition hosted by the National Institute of Standards and Technology (NIST). To deal with high-dimensional data, the distribution of synthetic data is represented by a probabilistic graphical model (e.g., a Bayesian network), while the raw data distribution is approximated by a collection of low-dimensional marginals. Differential privacy (DP) is guaranteed by introducing random noise to each low-dimensional marginal distribution. Despite its promising performance in practice, the statistical properties of marginal-based methods are rarely studied in the literature. In this paper, we study DP data synthesis algorithms based on Bayesian networks (BN) from a statistical perspective. We establish a rigorous accuracy guarantee for BN-based algorithms, where the errors are measured by the total variation (TV) distance or the $L^2$ distance. Related to downstream machine learning tasks, an upper bound for the utility error of the DP synthetic data is also derived. To complete the picture, we establish a lower bound for TV accuracy that holds for every $\epsilon$-DP synthetic data generator.

Double Matching Under Complementary Preferences

In this paper, we propose a new algorithm for addressing the problem of matching markets with complementary preferences, where agents' preferences are unknown a priori and must be learned from data. The presence of complementary preferences can lead to instability in the matching process, making this problem challenging to solve. To overcome this challenge, we formulate the problem as a bandit learning framework and propose the Multi-agent Multi-type Thompson Sampling (MMTS) algorithm. The algorithm combines the strengths of Thompson Sampling for exploration with a double matching technique to achieve a stable matching outcome. Our theoretical analysis demonstrates the effectiveness of MMTS as it is able to achieve stability at every matching step, satisfies the incentive-compatibility property, and has a sublinear Bayesian regret over time. Our approach provides a useful method for addressing complementary preferences in real-world scenarios.

Ranking Differential Privacy

Rankings are widely collected in various real-life scenarios, leading to the leakage of personal information such as users' preferences on videos or news. To protect rankings, existing works mainly develop privacy protection on a single ranking within a set of ranking or pairwise comparisons of a ranking under the $\epsilon$-differential privacy. This paper proposes a novel notion called $\epsilon$-ranking differential privacy for protecting ranks. We establish the connection between the Mallows model (Mallows, 1957) and the proposed $\epsilon$-ranking differential privacy. This allows us to develop a multistage ranking algorithm to generate synthetic rankings while satisfying the developed $\epsilon$-ranking differential privacy. Theoretical results regarding the utility of synthetic rankings in the downstream tasks, including the inference attack and the personalized ranking tasks, are established. For the inference attack, we quantify how $\epsilon$ affects the estimation of the true ranking based on synthetic rankings. For the personalized ranking task, we consider varying privacy preferences among users and quantify how their privacy preferences affect the consistency in estimating the optimal ranking function. Extensive numerical experiments are carried out to verify the theoretical results and demonstrate the effectiveness of the proposed synthetic ranking algorithm.

On the Utility Recovery Incapability of Neural Net-based Differential Private Tabular Training Data Synthesizer under Privacy Deregulation

Devising procedures for auditing generative model privacy-utility tradeoff is an important yet unresolved problem in practice. Existing works concentrates on investigating the privacy constraint side effect in terms of utility degradation of the train on synthetic, test on real paradigm of synthetic data training. We push such understanding on privacy-utility tradeoff to next level by observing the privacy deregulation side effect on synthetic training data utility. Surprisingly, we discover the Utility Recovery Incapability of DP-CTGAN and PATE-CTGAN under privacy deregulation, raising concerns on their practical applications. The main message is Privacy Deregulation does NOT always imply Utility Recovery.

Improving Adversarial Robustness by Contrastive Guided Diffusion Process

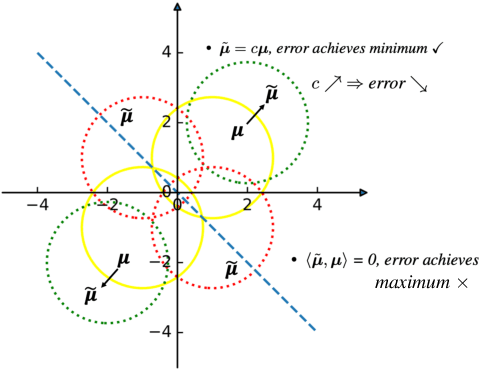
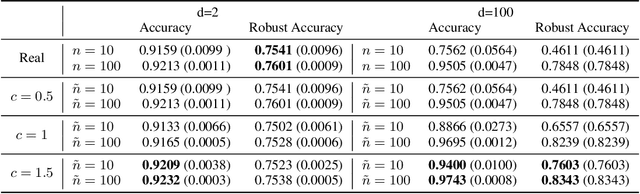
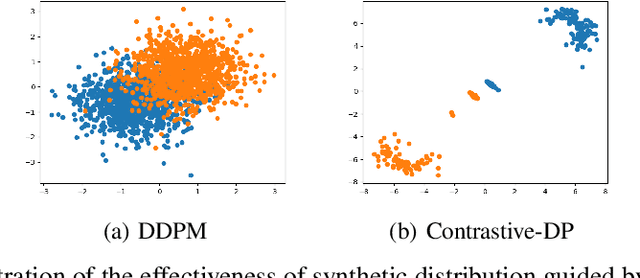
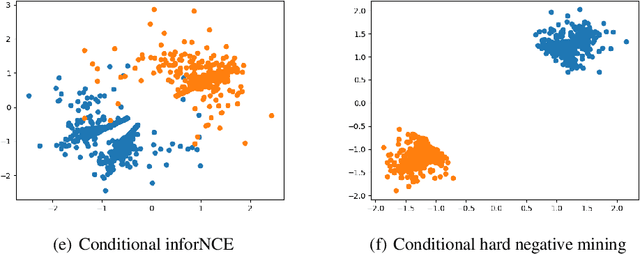
Synthetic data generation has become an emerging tool to help improve the adversarial robustness in classification tasks since robust learning requires a significantly larger amount of training samples compared with standard classification tasks. Among various deep generative models, the diffusion model has been shown to produce high-quality synthetic images and has achieved good performance in improving the adversarial robustness. However, diffusion-type methods are typically slow in data generation as compared with other generative models. Although different acceleration techniques have been proposed recently, it is also of great importance to study how to improve the sample efficiency of generated data for the downstream task. In this paper, we first analyze the optimality condition of synthetic distribution for achieving non-trivial robust accuracy. We show that enhancing the distinguishability among the generated data is critical for improving adversarial robustness. Thus, we propose the Contrastive-Guided Diffusion Process (Contrastive-DP), which adopts the contrastive loss to guide the diffusion model in data generation. We verify our theoretical results using simulations and demonstrate the good performance of Contrastive-DP on image datasets.

Differentially Private Bootstrap: New Privacy Analysis and Inference Strategies

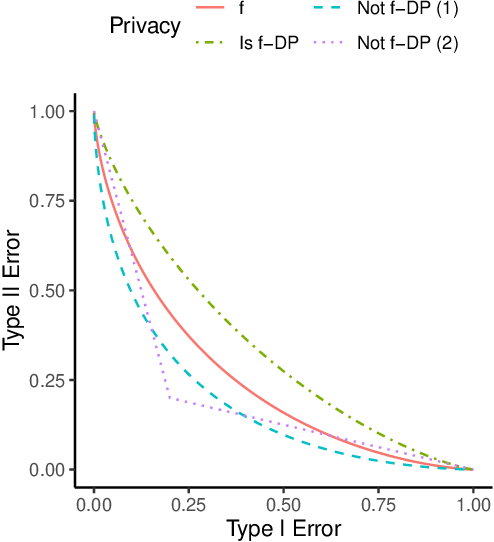
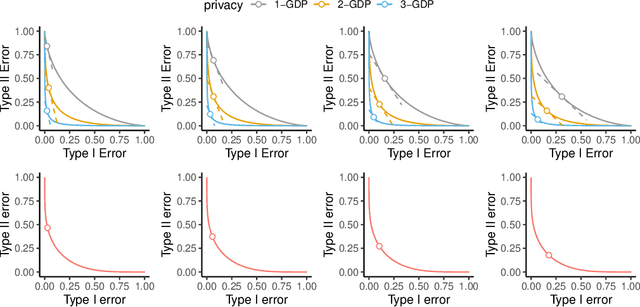
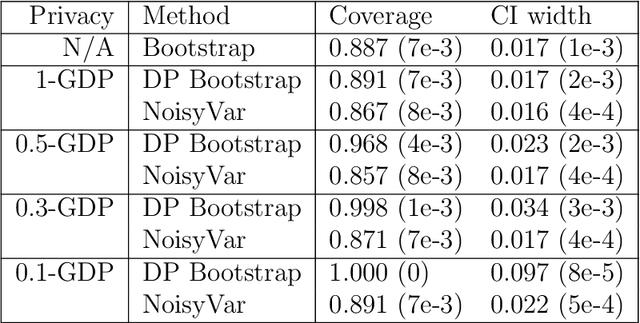
Differential private (DP) mechanisms protect individual-level information by introducing randomness into the statistical analysis procedure. While there are now many DP tools for various statistical problems, there is still a lack of general techniques to understand the sampling distribution of a DP estimator, which is crucial for uncertainty quantification in statistical inference. We analyze a DP bootstrap procedure that releases multiple private bootstrap estimates to infer the sampling distribution and construct confidence intervals. Our privacy analysis includes new results on the privacy cost of a single DP bootstrap estimate applicable to incorporate arbitrary DP mechanisms and identifies some misuses of the bootstrap in the existing literature. We show that the release of $B$ DP bootstrap estimates from mechanisms satisfying $(\mu/\sqrt{(2-2/\mathrm{e})B})$-Gaussian DP asymptotically satisfies $\mu$-Gaussian DP as $B$ goes to infinity. We also develop a statistical procedure based on the DP bootstrap estimates to correctly infer the sampling distribution using techniques related to the deconvolution of probability measures, an approach which is novel in analyzing DP procedures. From our density estimate, we construct confidence intervals and compare them to existing methods through simulations and real-world experiments using the 2016 Canada Census Public Use Microdata. The coverage of our private confidence intervals achieves the nominal confidence level, while other methods fail to meet this guarantee.

Fair Bayes-Optimal Classifiers Under Predictive Parity

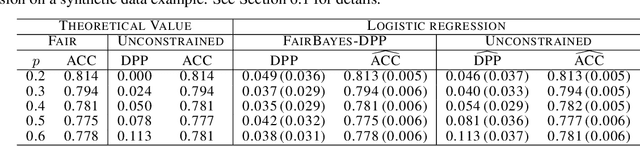
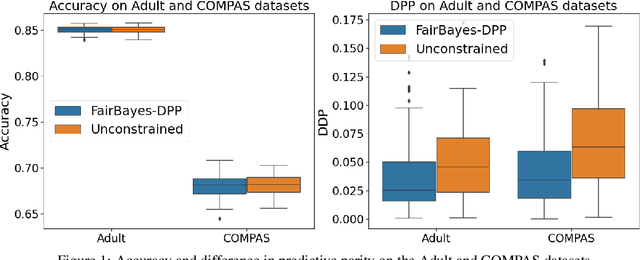
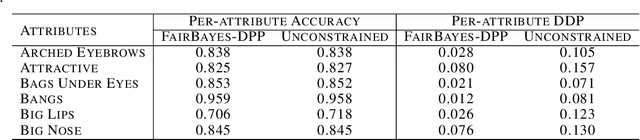
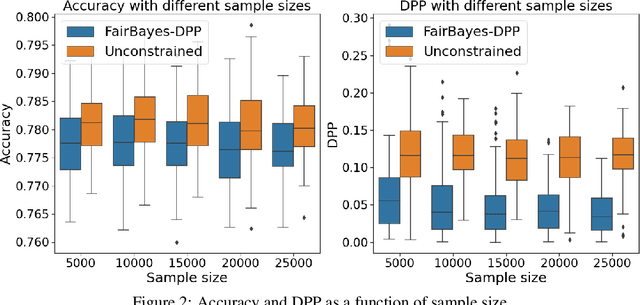
Increasing concerns about disparate effects of AI have motivated a great deal of work on fair machine learning. Existing works mainly focus on independence- and separation-based measures (e.g., demographic parity, equality of opportunity, equalized odds), while sufficiency-based measures such as predictive parity are much less studied. This paper considers predictive parity, which requires equalizing the probability of success given a positive prediction among different protected groups. We prove that, if the overall performances of different groups vary only moderately, all fair Bayes-optimal classifiers under predictive parity are group-wise thresholding rules. Perhaps surprisingly, this may not hold if group performance levels vary widely; in this case we find that predictive parity among protected groups may lead to within-group unfairness. We then propose an algorithm we call FairBayes-DPP, aiming to ensure predictive parity when our condition is satisfied. FairBayes-DPP is an adaptive thresholding algorithm that aims to achieve predictive parity, while also seeking to maximize test accuracy. We provide supporting experiments conducted on synthetic and empirical data.