Differentially Private Covariate Balancing Causal Inference

Differential privacy is the leading mathematical framework for privacy protection, providing a probabilistic guarantee that safeguards individuals' private information when publishing statistics from a dataset. This guarantee is achieved by applying a randomized algorithm to the original data, which introduces unique challenges in data analysis by distorting inherent patterns. In particular, causal inference using observational data in privacy-sensitive contexts is challenging because it requires covariate balance between treatment groups, yet checking the true covariates is prohibited to prevent leakage of sensitive information. In this article, we present a differentially private two-stage covariate balancing weighting estimator to infer causal effects from observational data. Our algorithm produces both point and interval estimators with statistical guarantees, such as consistency and rate optimality, under a given privacy budget.

Differentially Private Topological Data Analysis

This paper is the first to attempt differentially private (DP) topological data analysis (TDA), producing near-optimal private persistence diagrams. We analyze the sensitivity of persistence diagrams in terms of the bottleneck distance, and we show that the commonly used \v{C}ech complex has sensitivity that does not decrease as the sample size $n$ increases. This makes it challenging for the persistence diagrams of \v{C}ech complexes to be privatized. As an alternative, we show that the persistence diagram obtained by the $L^1$-distance to measure (DTM) has sensitivity $O(1/n)$. Based on the sensitivity analysis, we propose using the exponential mechanism whose utility function is defined in terms of the bottleneck distance of the $L^1$-DTM persistence diagrams. We also derive upper and lower bounds of the accuracy of our privacy mechanism; the obtained bounds indicate that the privacy error of our mechanism is near-optimal. We demonstrate the performance of our privatized persistence diagrams through simulations as well as on a real dataset tracking human movement.

Differentially Private Bootstrap: New Privacy Analysis and Inference Strategies

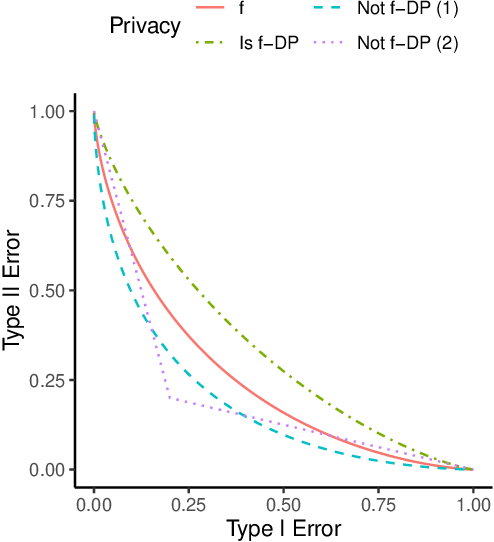
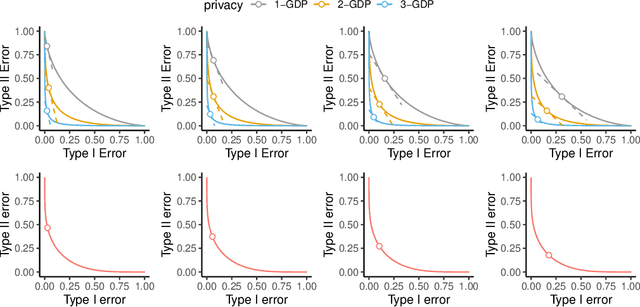
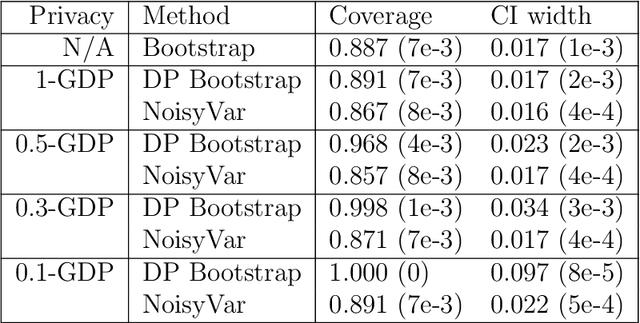
Differential private (DP) mechanisms protect individual-level information by introducing randomness into the statistical analysis procedure. While there are now many DP tools for various statistical problems, there is still a lack of general techniques to understand the sampling distribution of a DP estimator, which is crucial for uncertainty quantification in statistical inference. We analyze a DP bootstrap procedure that releases multiple private bootstrap estimates to infer the sampling distribution and construct confidence intervals. Our privacy analysis includes new results on the privacy cost of a single DP bootstrap estimate applicable to incorporate arbitrary DP mechanisms and identifies some misuses of the bootstrap in the existing literature. We show that the release of $B$ DP bootstrap estimates from mechanisms satisfying $(\mu/\sqrt{(2-2/\mathrm{e})B})$-Gaussian DP asymptotically satisfies $\mu$-Gaussian DP as $B$ goes to infinity. We also develop a statistical procedure based on the DP bootstrap estimates to correctly infer the sampling distribution using techniques related to the deconvolution of probability measures, an approach which is novel in analyzing DP procedures. From our density estimate, we construct confidence intervals and compare them to existing methods through simulations and real-world experiments using the 2016 Canada Census Public Use Microdata. The coverage of our private confidence intervals achieves the nominal confidence level, while other methods fail to meet this guarantee.

KNG: The K-Norm Gradient Mechanism

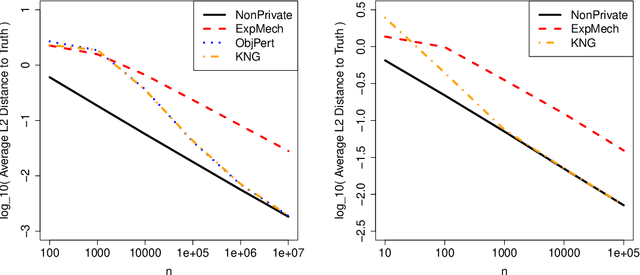
This paper presents a new mechanism for producing sanitized statistical summaries that achieve \emph{differential privacy}, called the \emph{K-Norm Gradient} Mechanism, or KNG. This new approach maintains the strong flexibility of the exponential mechanism, while achieving the powerful utility performance of objective perturbation. KNG starts with an inherent objective function (often an empirical risk), and promotes summaries that are close to minimizing the objective by weighting according to how far the gradient of the objective function is from zero. Working with the gradient instead of the original objective function allows for additional flexibility as one can penalize using different norms. We show that, unlike the exponential mechanism, the noise added by KNG is asymptotically negligible compared to the statistical error for many problems. In addition to theoretical guarantees on privacy and utility, we confirm the utility of KNG empirically in the settings of linear and quantile regression through simulations.

Benefits and Pitfalls of the Exponential Mechanism with Applications to Hilbert Spaces and Functional PCA

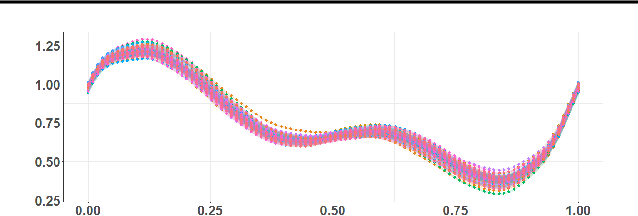
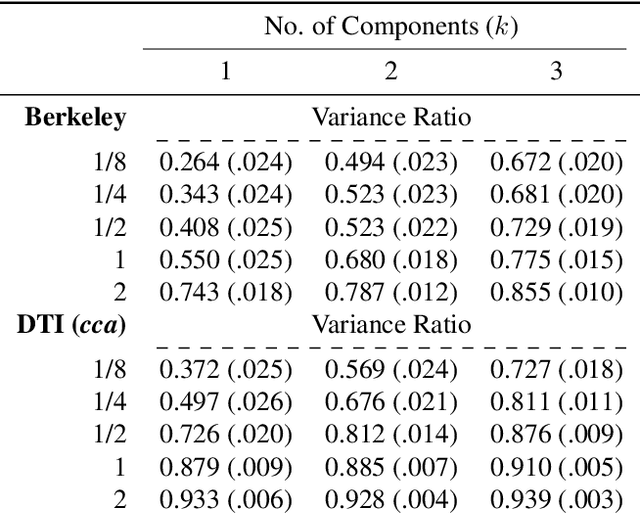
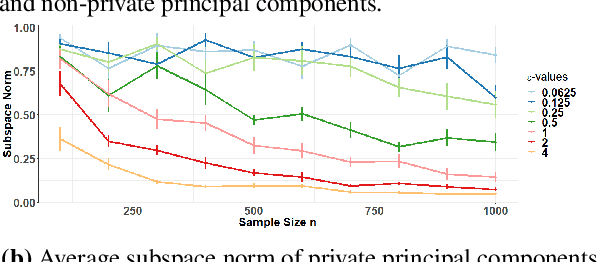
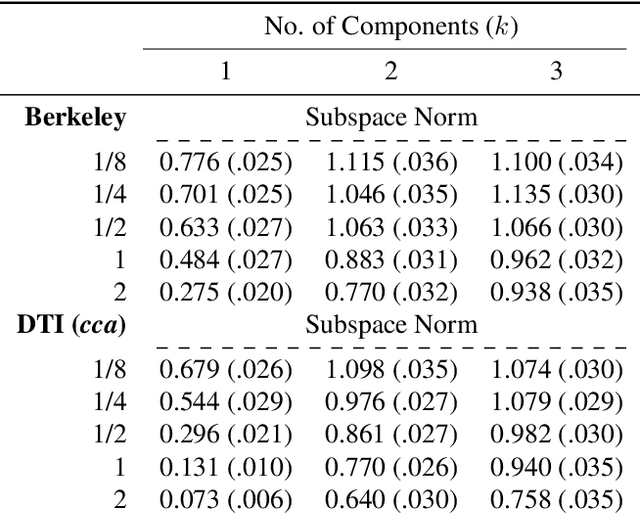
The exponential mechanism is a fundamental tool of Differential Privacy (DP) due to its strong privacy guarantees and flexibility. We study its extension to settings with summaries based on infinite dimensional outputs such as with functional data analysis, shape analysis, and nonparametric statistics. We show that one can design the mechanism with respect to a specific base measure over the output space, such as a Guassian process. We provide a positive result that establishes a Central Limit Theorem for the exponential mechanism quite broadly. We also provide an apparent negative result, showing that the magnitude of the noise introduced for privacy is asymptotically non-negligible relative to the statistical estimation error. We develop an \ep-DP mechanism for functional principal component analysis, applicable in separable Hilbert spaces. We demonstrate its performance via simulations and applications to two datasets.