Kolmogorov-Arnold Representation for Symplectic Learning: Advancing Hamiltonian Neural Networks

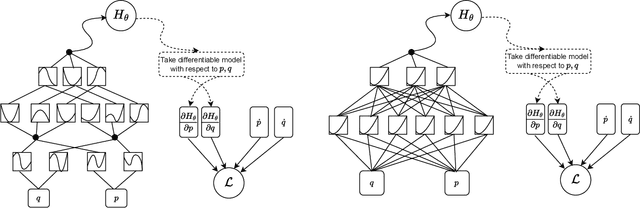
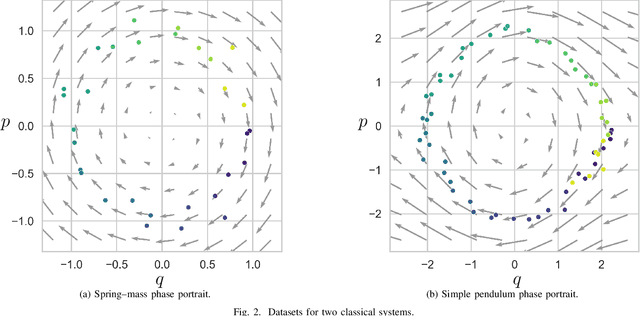
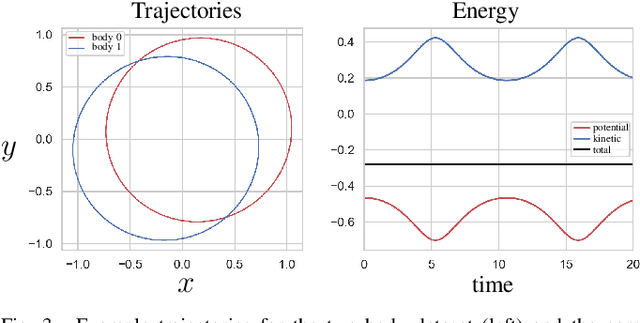
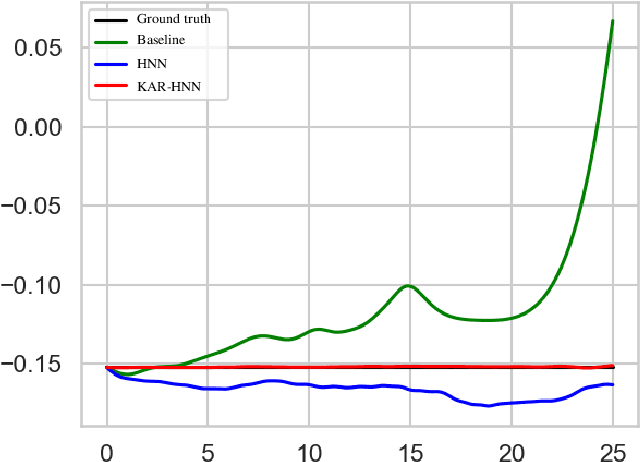
We propose a Kolmogorov-Arnold Representation-based Hamiltonian Neural Network (KAR-HNN) that replaces the Multilayer Perceptrons (MLPs) with univariate transformations. While Hamiltonian Neural Networks (HNNs) ensure energy conservation by learning Hamiltonian functions directly from data, existing implementations, often relying on MLPs, cause hypersensitivity to the hyperparameters while exploring complex energy landscapes. Our approach exploits the localized function approximations to better capture high-frequency and multi-scale dynamics, reducing energy drift and improving long-term predictive stability. The networks preserve the symplectic form of Hamiltonian systems, and thus maintain interpretability and physical consistency. After assessing KAR-HNN on four benchmark problems including spring-mass, simple pendulum, two- and three-body problem, we foresee its effectiveness for accurate and stable modeling of realistic physical processes often at high dimensions and with few known parameters.

An Iterative Framework for Generative Backmapping of Coarse Grained Proteins

The techniques of data-driven backmapping from coarse-grained (CG) to fine-grained (FG) representation often struggle with accuracy, unstable training, and physical realism, especially when applied to complex systems such as proteins. In this work, we introduce a novel iterative framework by using conditional Variational Autoencoders and graph-based neural networks, specifically designed to tackle the challenges associated with such large-scale biomolecules. Our method enables stepwise refinement from CG beads to full atomistic details. We outline the theory of iterative generative backmapping and demonstrate via numerical experiments the advantages of multistep schemes by applying them to proteins of vastly different structures with very coarse representations. This multistep approach not only improves the accuracy of reconstructions but also makes the training process more computationally efficient for proteins with ultra-CG representations.