Kolmogorov-Arnold Representation for Symplectic Learning: Advancing Hamiltonian Neural Networks

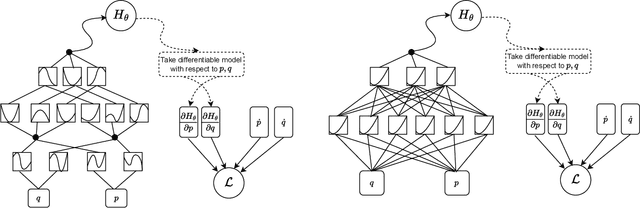
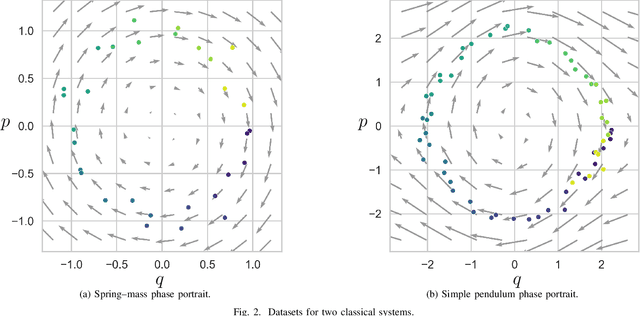
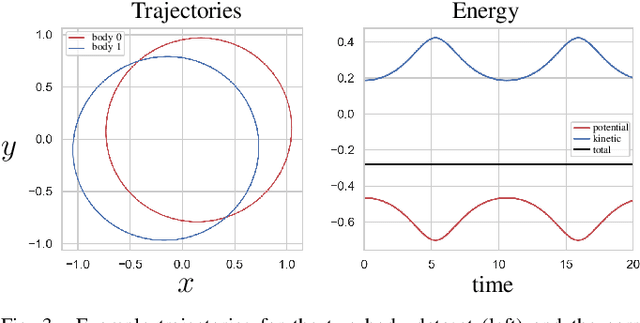
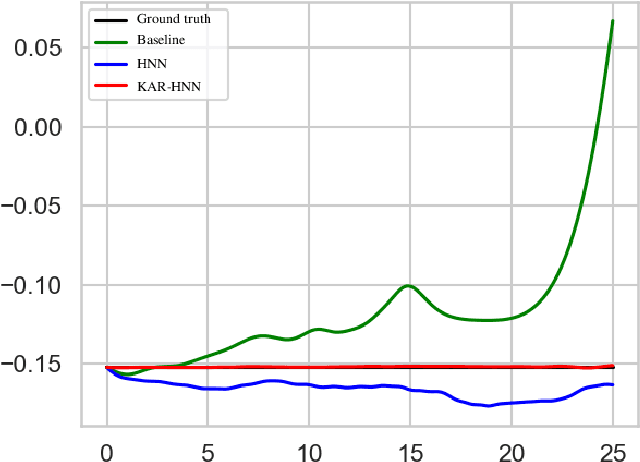
We propose a Kolmogorov-Arnold Representation-based Hamiltonian Neural Network (KAR-HNN) that replaces the Multilayer Perceptrons (MLPs) with univariate transformations. While Hamiltonian Neural Networks (HNNs) ensure energy conservation by learning Hamiltonian functions directly from data, existing implementations, often relying on MLPs, cause hypersensitivity to the hyperparameters while exploring complex energy landscapes. Our approach exploits the localized function approximations to better capture high-frequency and multi-scale dynamics, reducing energy drift and improving long-term predictive stability. The networks preserve the symplectic form of Hamiltonian systems, and thus maintain interpretability and physical consistency. After assessing KAR-HNN on four benchmark problems including spring-mass, simple pendulum, two- and three-body problem, we foresee its effectiveness for accurate and stable modeling of realistic physical processes often at high dimensions and with few known parameters.