Decentralized Sensor Fusion With Distributed Particle Filters

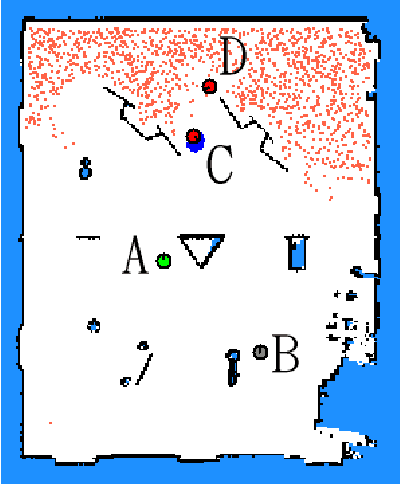
This paper presents a scalable Bayesian technique for decentralized state estimation from multiple platforms in dynamic environments. As has long been recognized, centralized architectures impose severe scaling limitations for distributed systems due to the enormous communication overheads. We propose a strictly decentralized approach in which only nearby platforms exchange information. They do so through an interactive communication protocol aimed at maximizing information flow. Our approach is evaluated in the context of a distributed surveillance scenario that arises in a robotic system for playing the game of laser tag. Our results, both from simulation and using physical robots, illustrate an unprecedented scaling capability to large teams of vehicles.

Policy-contingent abstraction for robust robot control

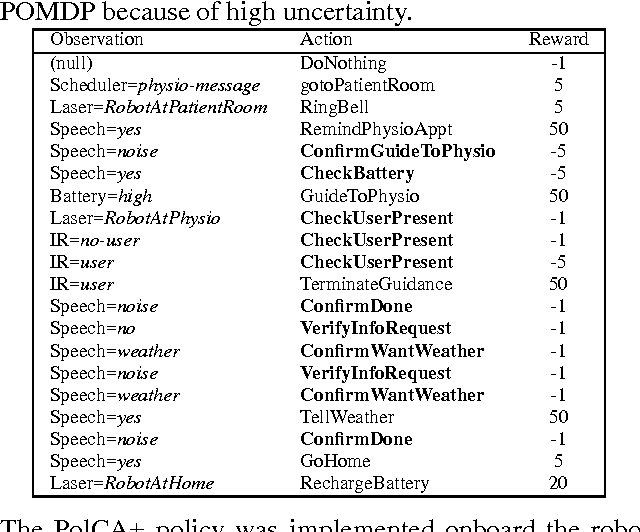
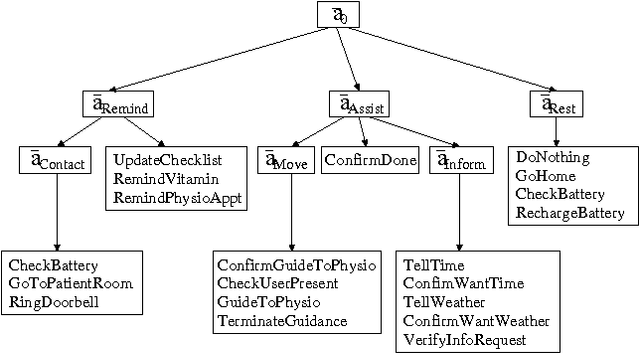
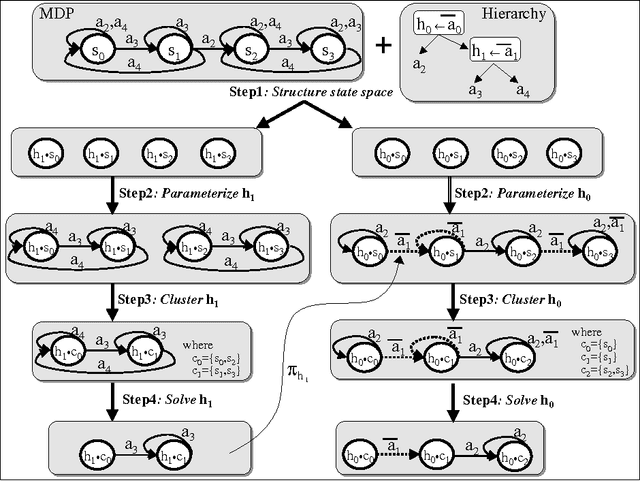
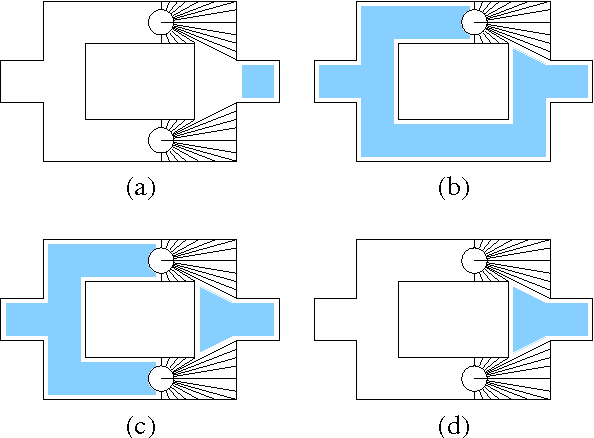
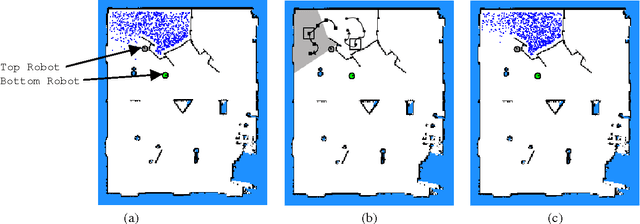
This paper presents a scalable control algorithm that enables a deployed mobile robot system to make high-level decisions under full consideration of its probabilistic belief. Our approach is based on insights from the rich literature of hierarchical controllers and hierarchical MDPs. The resulting controller has been successfully deployed in a nursing facility near Pittsburgh, PA. To the best of our knowledge, this work is a unique instance of applying POMDPs to high-level robotic control problems.

First-Order Mixed Integer Linear Programming

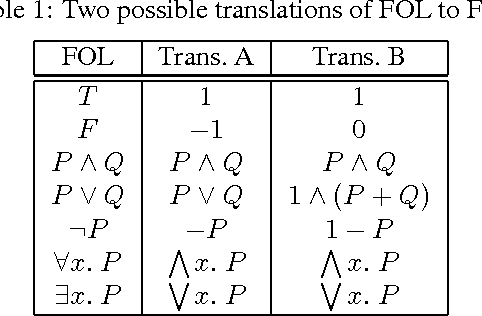
Mixed integer linear programming (MILP) is a powerful representation often used to formulate decision-making problems under uncertainty. However, it lacks a natural mechanism to reason about objects, classes of objects, and relations. First-order logic (FOL), on the other hand, excels at reasoning about classes of objects, but lacks a rich representation of uncertainty. While representing propositional logic in MILP has been extensively explored, no theory exists yet for fully combining FOL with MILP. We propose a new representation, called first-order programming or FOP, which subsumes both FOL and MILP. We establish formal methods for reasoning about first order programs, including a sound and complete lifted inference procedure for integer first order programs. Since FOP can offer exponential savings in representation and proof size compared to FOL, and since representations and proofs are never significantly longer in FOP than in FOL, we anticipate that inference in FOP will be more tractable than inference in FOL for corresponding problems.

A Bayesian Matrix Factorization Model for Relational Data

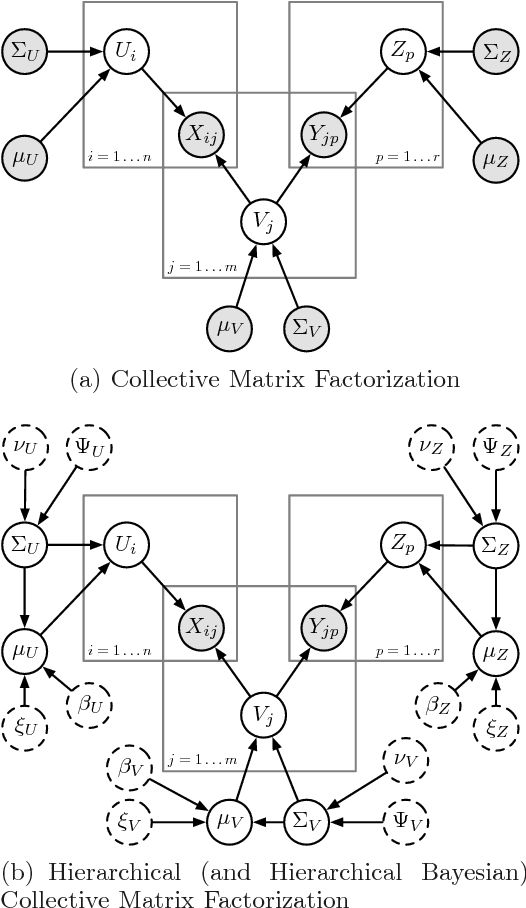
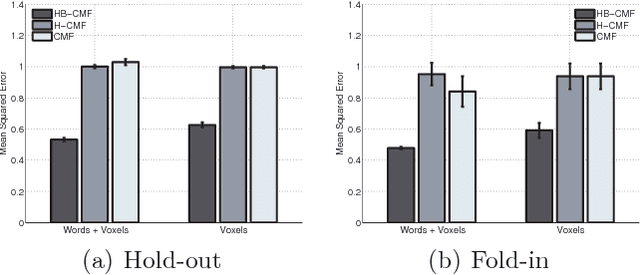
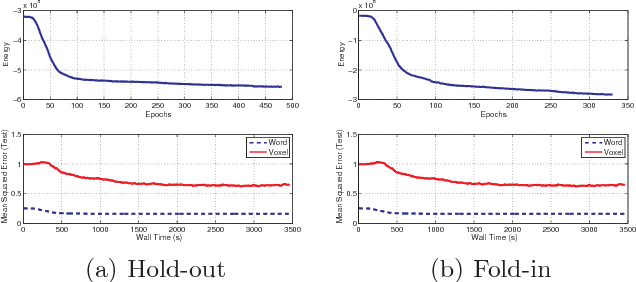
Relational learning can be used to augment one data source with other correlated sources of information, to improve predictive accuracy. We frame a large class of relational learning problems as matrix factorization problems, and propose a hierarchical Bayesian model. Training our Bayesian model using random-walk Metropolis-Hastings is impractically slow, and so we develop a block Metropolis-Hastings sampler which uses the gradient and Hessian of the likelihood to dynamically tune the proposal. We demonstrate that a predictive model of brain response to stimuli can be improved by augmenting it with side information about the stimuli.