A Path to Universal Neural Cellular Automata

Cellular automata have long been celebrated for their ability to generate complex behaviors from simple, local rules, with well-known discrete models like Conway's Game of Life proven capable of universal computation. Recent advancements have extended cellular automata into continuous domains, raising the question of whether these systems retain the capacity for universal computation. In parallel, neural cellular automata have emerged as a powerful paradigm where rules are learned via gradient descent rather than manually designed. This work explores the potential of neural cellular automata to develop a continuous Universal Cellular Automaton through training by gradient descent. We introduce a cellular automaton model, objective functions and training strategies to guide neural cellular automata toward universal computation in a continuous setting. Our experiments demonstrate the successful training of fundamental computational primitives - such as matrix multiplication and transposition - culminating in the emulation of a neural network solving the MNIST digit classification task directly within the cellular automata state. These results represent a foundational step toward realizing analog general-purpose computers, with implications for understanding universal computation in continuous dynamics and advancing the automated discovery of complex cellular automata behaviors via machine learning.

Deep-Unrolling Multidimensional Harmonic Retrieval Algorithms on Neuromorphic Hardware

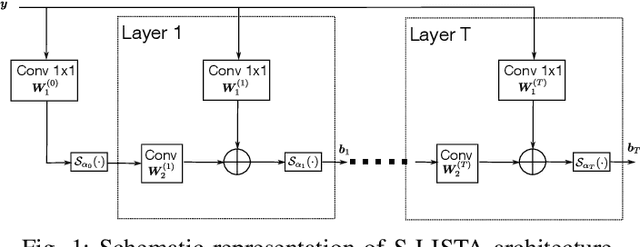
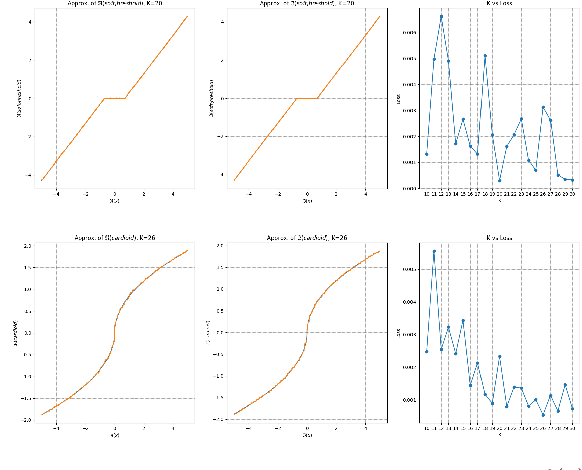
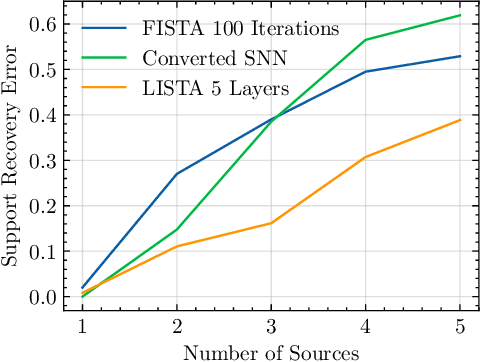
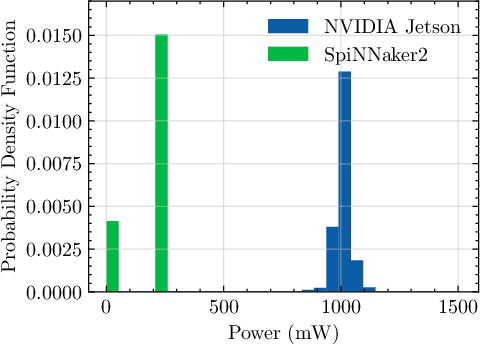
This paper explores the potential of conversion-based neuromorphic algorithms for highly accurate and energy-efficient single-snapshot multidimensional harmonic retrieval (MHR). By casting the MHR problem as a sparse recovery problem, we devise the currently proposed, deep-unrolling-based Structured Learned Iterative Shrinkage and Thresholding (S-LISTA) algorithm to solve it efficiently using complex-valued convolutional neural networks with complex-valued activations, which are trained using a supervised regression objective. Afterward, a novel method for converting the complex-valued convolutional layers and activations into spiking neural networks (SNNs) is developed. At the heart of this method lies the recently proposed Few Spikes (FS) conversion, which is extended by modifying the neuron model's parameters and internal dynamics to account for the inherent coupling between real and imaginary parts in complex-valued computations. Finally, the converted SNNs are mapped onto the SpiNNaker2 neuromorphic board, and a comparison in terms of estimation accuracy and power efficiency between the original CNNs deployed on an NVIDIA Jetson Xavier and the SNNs is being conducted. The measurement results show that the converted SNNs achieve almost five-fold power efficiency at moderate performance loss compared to the original CNNs.

Extreme sparsity gives rise to functional specialization

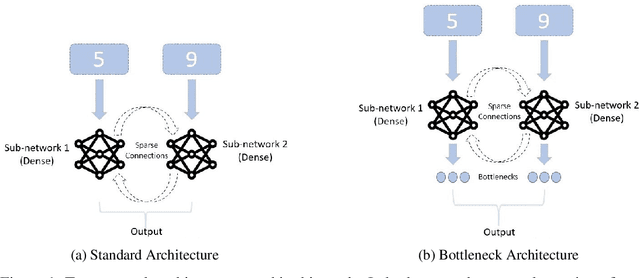
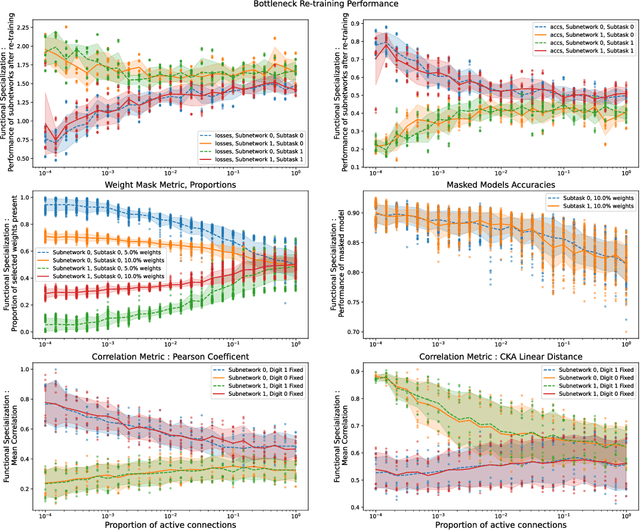
Modularity of neural networks -- both biological and artificial -- can be thought of either structurally or functionally, and the relationship between these is an open question. We show that enforcing structural modularity via sparse connectivity between two dense sub-networks which need to communicate to solve the task leads to functional specialization of the sub-networks, but only at extreme levels of sparsity. With even a moderate number of interconnections, the sub-networks become functionally entangled. Defining functional specialization is in itself a challenging problem without a universally agreed solution. To address this, we designed three different measures of specialization (based on weight masks, retraining and correlation) and found them to qualitatively agree. Our results have implications in both neuroscience and machine learning. For neuroscience, it shows that we cannot conclude that there is functional modularity simply by observing moderate levels of structural modularity: knowing the brain's connectome is not sufficient for understanding how it breaks down into functional modules. For machine learning, using structure to promote functional modularity -- which may be important for robustness and generalization -- may require extremely narrow bottlenecks between modules.