Certified Neural Approximations of Nonlinear Dynamics

Neural networks hold great potential to act as approximate models of nonlinear dynamical systems, with the resulting neural approximations enabling verification and control of such systems. However, in safety-critical contexts, the use of neural approximations requires formal bounds on their closeness to the underlying system. To address this fundamental challenge, we propose a novel, adaptive, and parallelizable verification method based on certified first-order models. Our approach provides formal error bounds on the neural approximations of dynamical systems, allowing them to be safely employed as surrogates by interpreting the error bound as bounded disturbances acting on the approximated dynamics. We demonstrate the effectiveness and scalability of our method on a range of established benchmarks from the literature, showing that it outperforms the state-of-the-art. Furthermore, we highlight the flexibility of our framework by applying it to two novel scenarios not previously explored in this context: neural network compression and an autoencoder-based deep learning architecture for learning Koopman operators, both yielding compelling results.

Realistic Adversarial Attacks for Robustness Evaluation of Trajectory Prediction Models via Future State Perturbation

Trajectory prediction is a key element of autonomous vehicle systems, enabling them to anticipate and react to the movements of other road users. Evaluating the robustness of prediction models against adversarial attacks is essential to ensure their reliability in real-world traffic. However, current approaches tend to focus on perturbing the past positions of surrounding agents, which can generate unrealistic scenarios and overlook critical vulnerabilities. This limitation may result in overly optimistic assessments of model performance in real-world conditions. In this work, we demonstrate that perturbing not just past but also future states of adversarial agents can uncover previously undetected weaknesses and thereby provide a more rigorous evaluation of model robustness. Our novel approach incorporates dynamic constraints and preserves tactical behaviors, enabling more effective and realistic adversarial attacks. We introduce new performance measures to assess the realism and impact of these adversarial trajectories. Testing our method on a state-of-the-art prediction model revealed significant increases in prediction errors and collision rates under adversarial conditions. Qualitative analysis further showed that our attacks can expose critical weaknesses, such as the inability of the model to detect potential collisions in what appear to be safe predictions. These results underscore the need for more comprehensive adversarial testing to better evaluate and improve the reliability of trajectory prediction models for autonomous vehicles.

Data-Driven Permissible Safe Control with Barrier Certificates

This paper introduces a method of identifying a maximal set of safe strategies from data for stochastic systems with unknown dynamics using barrier certificates. The first step is learning the dynamics of the system via Gaussian process (GP) regression and obtaining probabilistic errors for this estimate. Then, we develop an algorithm for constructing piecewise stochastic barrier functions to find a maximal permissible strategy set using the learned GP model, which is based on sequentially pruning the worst controls until a maximal set is identified. The permissible strategies are guaranteed to maintain probabilistic safety for the true system. This is especially important for learning-enabled systems, because a rich strategy space enables additional data collection and complex behaviors while remaining safe. Case studies on linear and nonlinear systems demonstrate that increasing the size of the dataset for learning the system grows the permissible strategy set.

Piecewise Stochastic Barrier Functions

This paper presents a novel stochastic barrier function (SBF) framework for safety analysis of stochastic systems based on piecewise (PW) functions. We first outline a general formulation of PW-SBFs. Then, we focus on PW-Constant (PWC) SBFs and show how their simplicity yields computational advantages for general stochastic systems. Specifically, we prove that synthesis of PWC-SBFs reduces to a minimax optimization problem. Then, we introduce three efficient algorithms to solve this problem, each offering distinct advantages and disadvantages. The first algorithm is based on dual linear programming (LP), which provides an exact solution to the minimax optimization problem. The second is a more scalable algorithm based on iterative counter-example guided synthesis, which involves solving two smaller LPs. The third algorithm solves the minimax problem using gradient descent, which admits even better scalability. We provide an extensive evaluation of these methods on various case studies, including neural network dynamic models, nonlinear switched systems, and high-dimensional linear systems. Our benchmarks demonstrate that PWC-SBFs outperform state-of-the-art methods, namely sum-of-squares and neural barrier functions, and can scale to eight dimensional systems.

A survey on robustness in trajectory prediction for autonomous vehicles

Autonomous vehicles rely on accurate trajectory prediction to inform decision-making processes related to navigation and collision avoidance. However, current trajectory prediction models show signs of overfitting, which may lead to unsafe or suboptimal behavior. To address these challenges, this paper presents a comprehensive framework that categorizes and assesses the definitions and strategies used in the literature on evaluating and improving the robustness of trajectory prediction models. This involves a detailed exploration of various approaches, including data slicing methods, perturbation techniques, model architecture changes, and post-training adjustments. In the literature, we see many promising methods for increasing robustness, which are necessary for safe and reliable autonomous driving.

Safety Certification for Stochastic Systems via Neural Barrier Functions

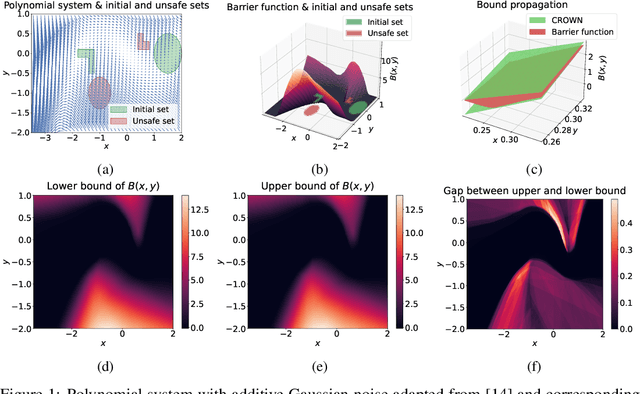
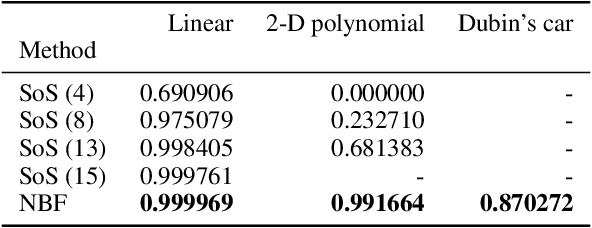
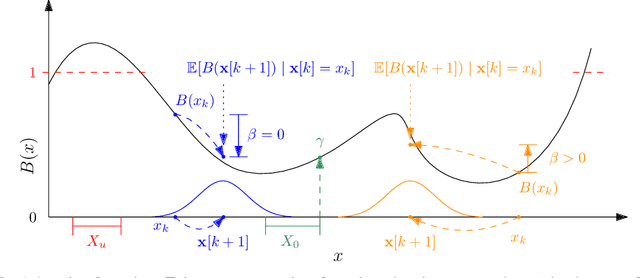
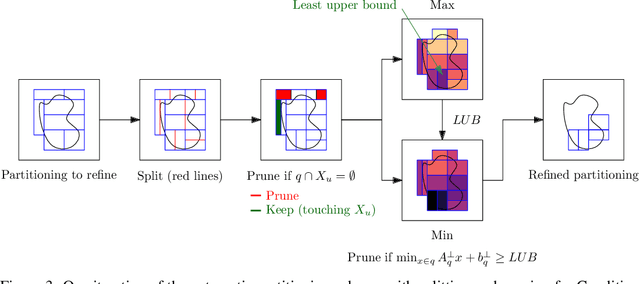
Providing non-trivial certificates of safety for non-linear stochastic systems is an important open problem that limits the wider adoption of autonomous systems in safety-critical applications. One promising solution to address this problem is barrier functions. The composition of a barrier function with a stochastic system forms a supermartingale, thus enabling the computation of the probability that the system stays in a safe set over a finite time horizon via martingale inequalities. However, existing approaches to find barrier functions for stochastic systems generally rely on convex optimization programs that restrict the search of a barrier to a small class of functions such as low degree SoS polynomials and can be computationally expensive. In this paper, we parameterize a barrier function as a neural network and show that techniques for robust training of neural networks can be successfully employed to find neural barrier functions. Specifically, we leverage bound propagation techniques to certify that a neural network satisfies the conditions to be a barrier function via linear programming and then employ the resulting bounds at training time to enforce the satisfaction of these conditions. We also present a branch-and-bound scheme that makes the certification framework scalable. We show that our approach outperforms existing methods in several case studies and often returns certificates of safety that are orders of magnitude larger.