Controlling for discrete unmeasured confounding in nonlinear causal models

Unmeasured confounding is a major challenge for identifying causal relationships from non-experimental data. Here, we propose a method that can accommodate unmeasured discrete confounding. Extending recent identifiability results in deep latent variable models, we show theoretically that confounding can be detected and corrected under the assumption that the observed data is a piecewise affine transformation of a latent Gaussian mixture model and that the identity of the mixture components is confounded. We provide a flow-based algorithm to estimate this model and perform deconfounding. Experimental results on synthetic and real-world data provide support for the effectiveness of our approach.

Approximate Causal Abstraction

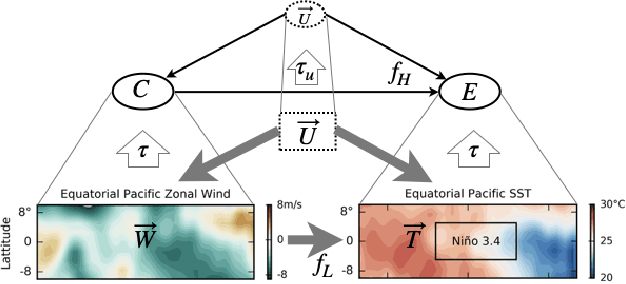
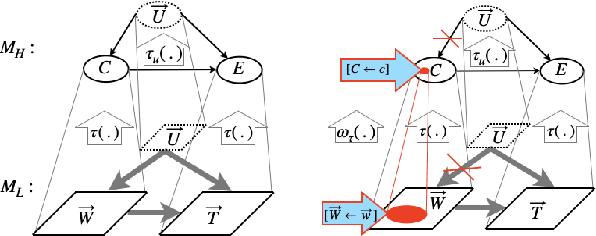
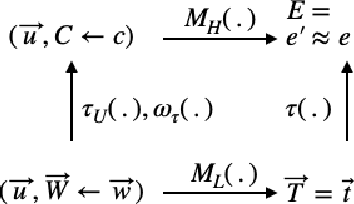
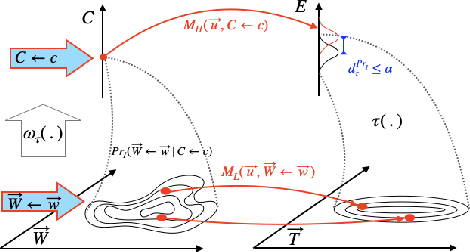
Scientific models describe natural phenomena at different levels of abstraction. Abstract descriptions can provide the basis for interventions on the system and explanation of observed phenomena at a level of granularity that is coarser than the most fundamental account of the system. Beckers and Halpern (2019), building on work of Rubenstein et al. (2017), developed an account of abstraction for causal models that is exact. Here we extend this account to the more realistic case where an abstract causal model offers only an approximation of the underlying system. We show how the resulting account handles the discrepancy that can arise between low- and high-level causal models of the same system, and in the process provide an account of how one causal model approximates another, a topic of independent interest. Finally, we extend the account of approximate abstractions to probabilistic causal models, indicating how and where uncertainty can enter into an approximate abstraction.

ASP-based Discovery of Semi-Markovian Causal Models under Weaker Assumptions

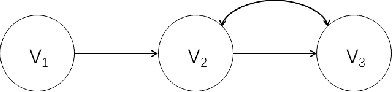
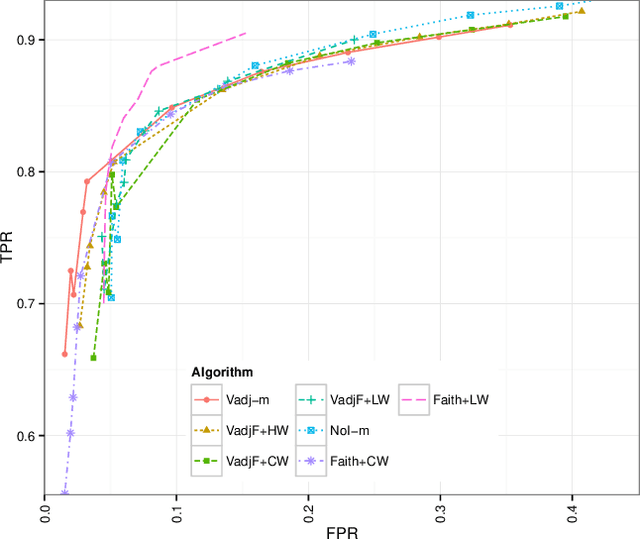
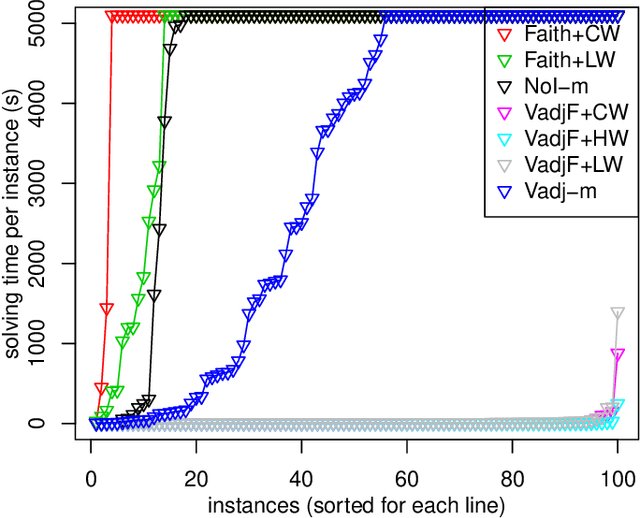
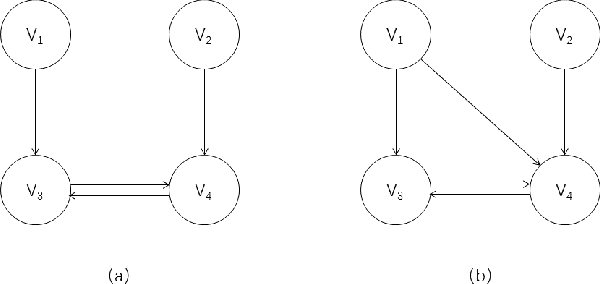
In recent years the possibility of relaxing the so-called Faithfulness assumption in automated causal discovery has been investigated. The investigation showed (1) that the Faithfulness assumption can be weakened in various ways that in an important sense preserve its power, and (2) that weakening of Faithfulness may help to speed up methods based on Answer Set Programming. However, this line of work has so far only considered the discovery of causal models without latent variables. In this paper, we study weakenings of Faithfulness for constraint-based discovery of semi-Markovian causal models, which accommodate the possibility of latent variables, and show that both (1) and (2) remain the case in this more realistic setting.

Fast Conditional Independence Test for Vector Variables with Large Sample Sizes

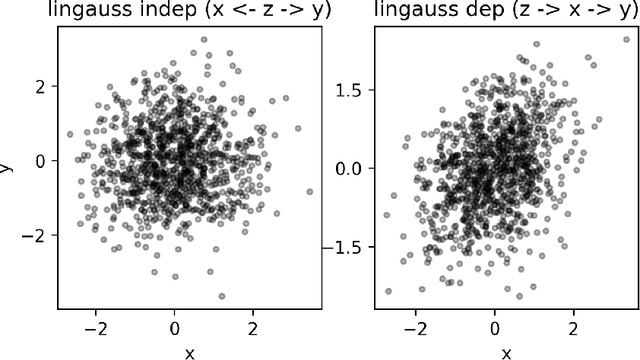
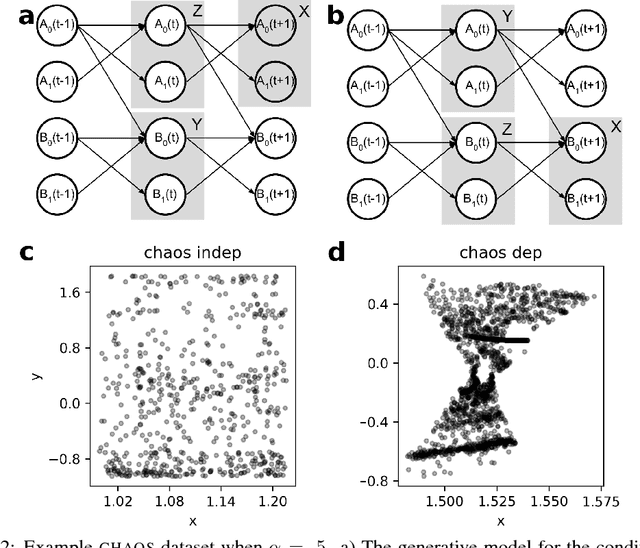
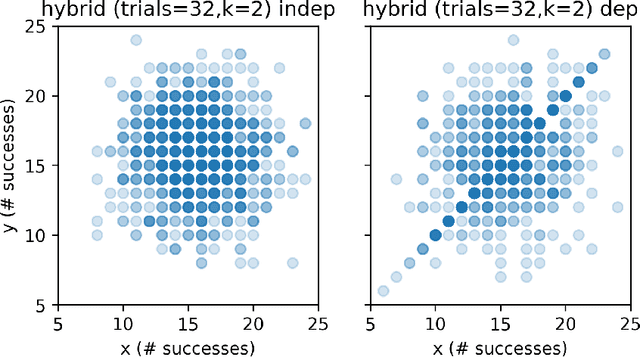
We present and evaluate the Fast (conditional) Independence Test (FIT) -- a nonparametric conditional independence test. The test is based on the idea that when $P(X \mid Y, Z) = P(X \mid Y)$, $Z$ is not useful as a feature to predict $X$, as long as $Y$ is also a regressor. On the contrary, if $P(X \mid Y, Z) \neq P(X \mid Y)$, $Z$ might improve prediction results. FIT applies to thousand-dimensional random variables with a hundred thousand samples in a fraction of the time required by alternative methods. We provide an extensive evaluation that compares FIT to six extant nonparametric independence tests. The evaluation shows that FIT has low probability of making both Type I and Type II errors compared to other tests, especially as the number of available samples grows. Our implementation of FIT is publicly available.

Estimating Causal Direction and Confounding of Two Discrete Variables

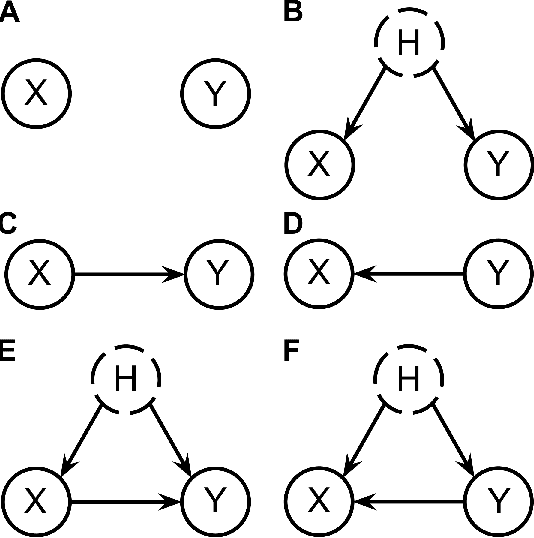
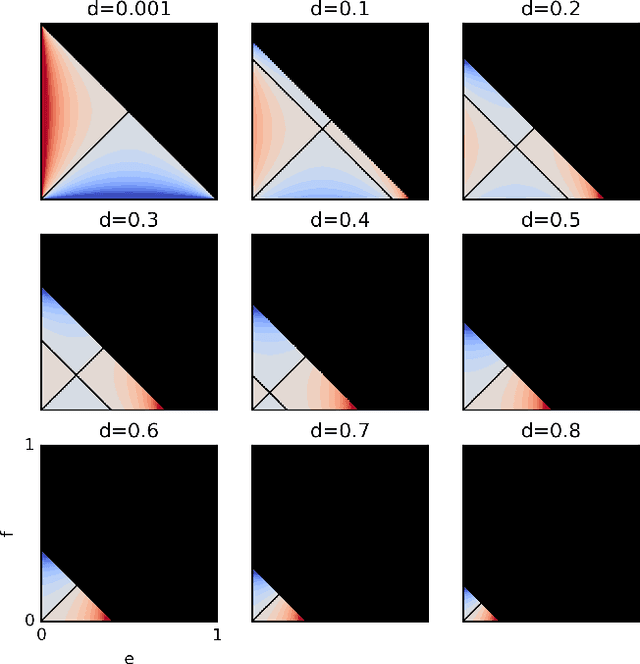
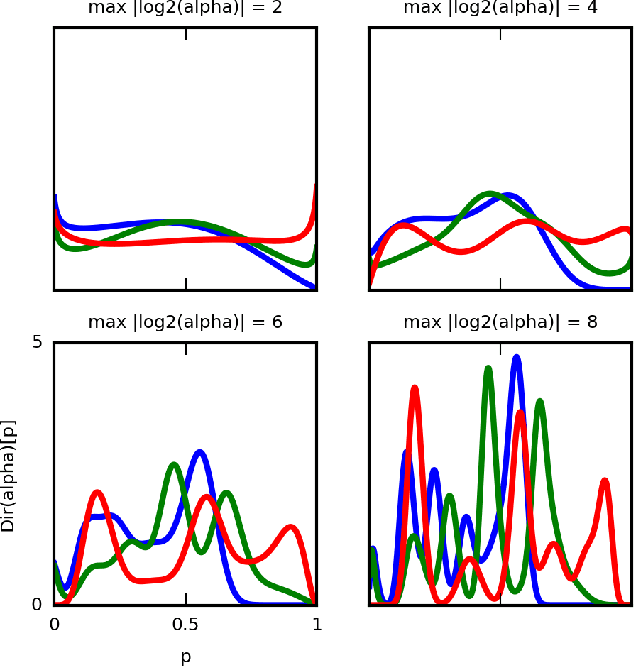
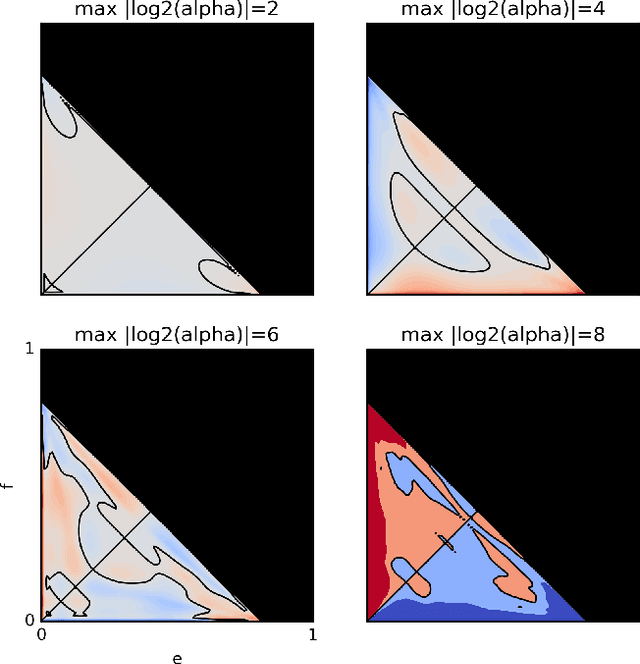
We propose a method to classify the causal relationship between two discrete variables given only the joint distribution of the variables, acknowledging that the method is subject to an inherent baseline error. We assume that the causal system is acyclicity, but we do allow for hidden common causes. Our algorithm presupposes that the probability distributions $P(C)$ of a cause $C$ is independent from the probability distribution $P(E\mid C)$ of the cause-effect mechanism. While our classifier is trained with a Bayesian assumption of flat hyperpriors, we do not make this assumption about our test data. This work connects to recent developments on the identifiability of causal models over continuous variables under the assumption of "independent mechanisms". Carefully-commented Python notebooks that reproduce all our experiments are available online at http://vision.caltech.edu/~kchalupk/code.html.

Causal Discovery from Subsampled Time Series Data by Constraint Optimization

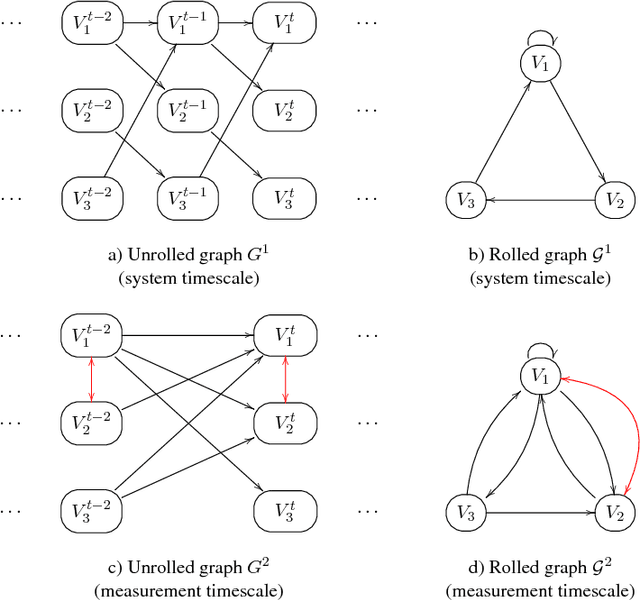
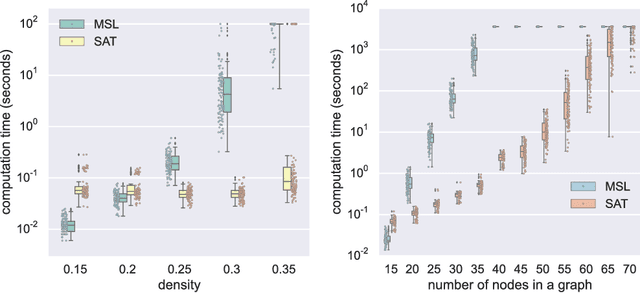
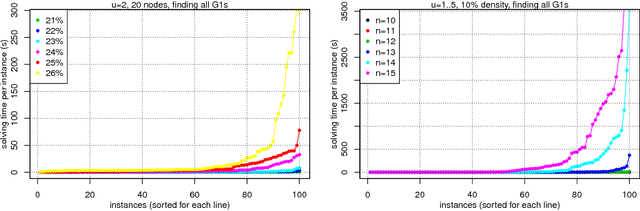
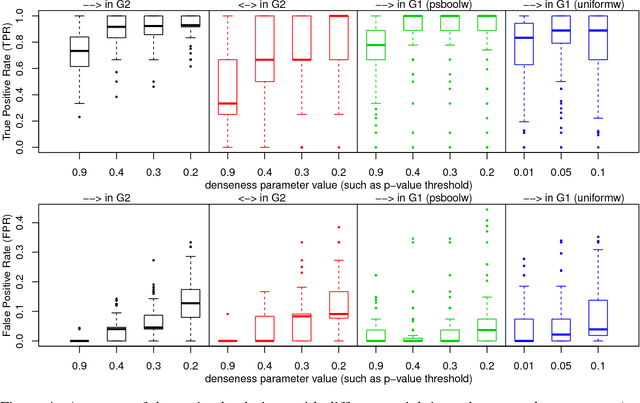
This paper focuses on causal structure estimation from time series data in which measurements are obtained at a coarser timescale than the causal timescale of the underlying system. Previous work has shown that such subsampling can lead to significant errors about the system's causal structure if not properly taken into account. In this paper, we first consider the search for the system timescale causal structures that correspond to a given measurement timescale structure. We provide a constraint satisfaction procedure whose computational performance is several orders of magnitude better than previous approaches. We then consider finite-sample data as input, and propose the first constraint optimization approach for recovering the system timescale causal structure. This algorithm optimally recovers from possible conflicts due to statistical errors. More generally, these advances allow for a robust and non-parametric estimation of system timescale causal structures from subsampled time series data.

Unsupervised Discovery of El Nino Using Causal Feature Learning on Microlevel Climate Data

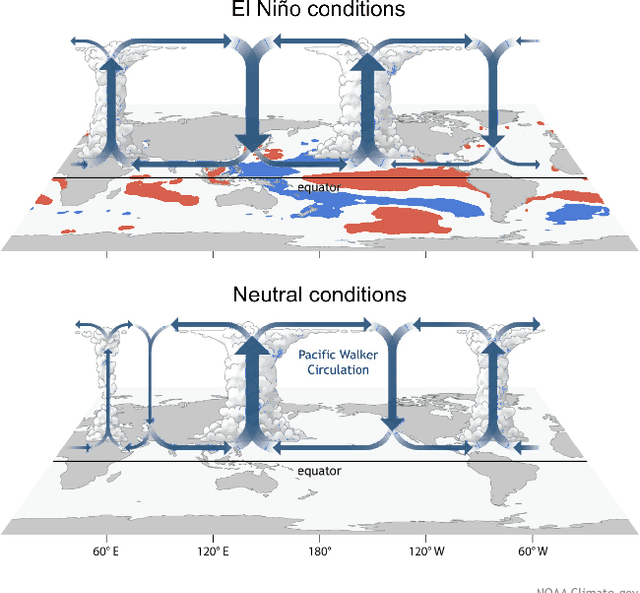
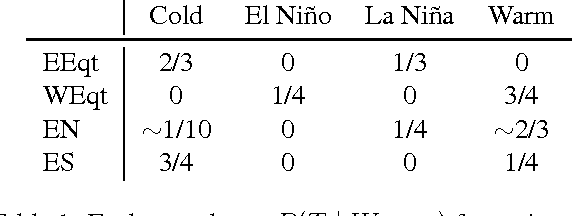
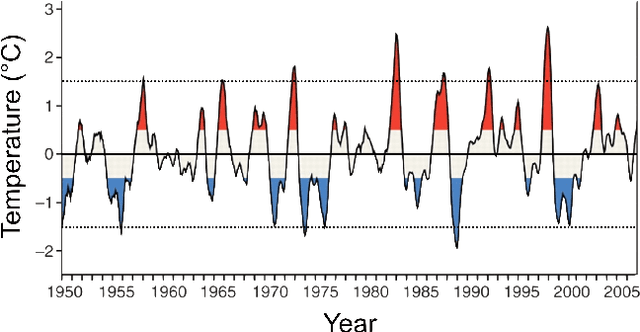
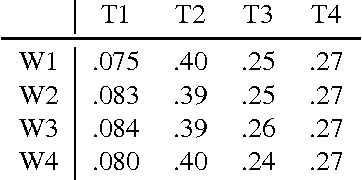
We show that the climate phenomena of El Nino and La Nina arise naturally as states of macro-variables when our recent causal feature learning framework (Chalupka 2015, Chalupka 2016) is applied to micro-level measures of zonal wind (ZW) and sea surface temperatures (SST) taken over the equatorial band of the Pacific Ocean. The method identifies these unusual climate states on the basis of the relation between ZW and SST patterns without any input about past occurrences of El Nino or La Nina. The simpler alternatives of (i) clustering the SST fields while disregarding their relationship with ZW patterns, or (ii) clustering the joint ZW-SST patterns, do not discover El Nino. We discuss the degree to which our method supports a causal interpretation and use a low-dimensional toy example to explain its success over other clustering approaches. Finally, we propose a new robust and scalable alternative to our original algorithm (Chalupka 2016), which circumvents the need for high-dimensional density learning.

Multi-Level Cause-Effect Systems

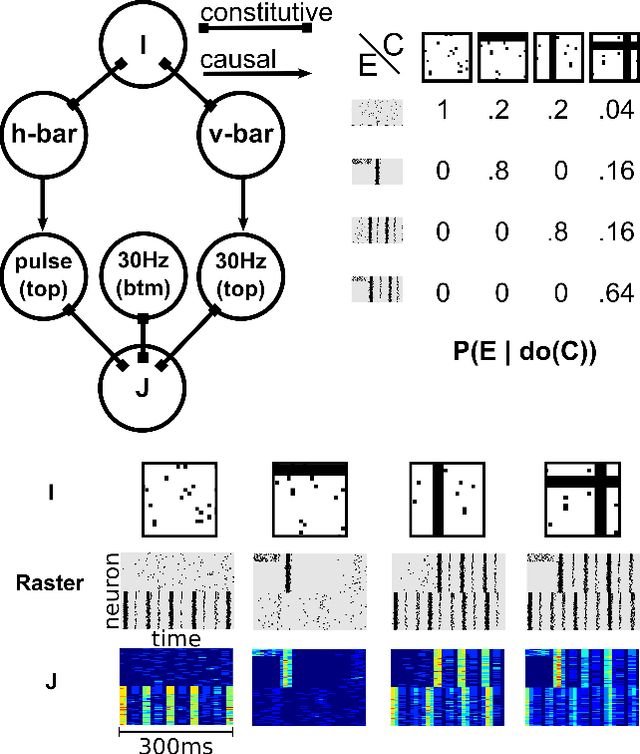
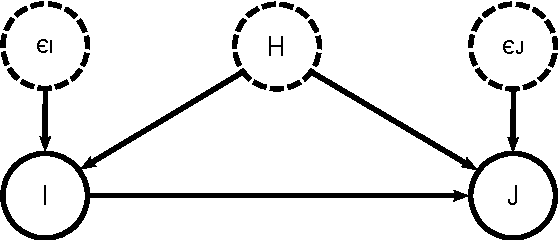
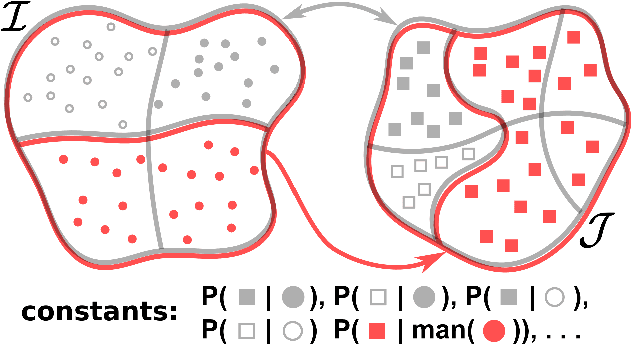
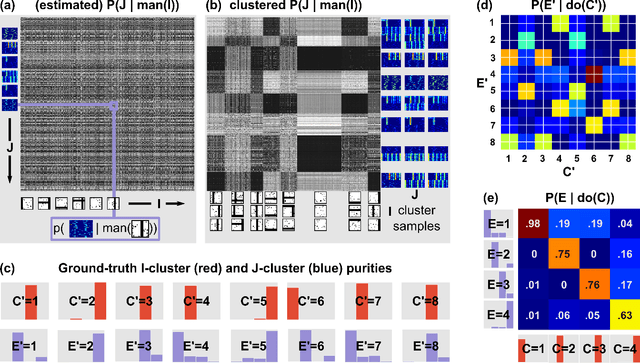
We present a domain-general account of causation that applies to settings in which macro-level causal relations between two systems are of interest, but the relevant causal features are poorly understood and have to be aggregated from vast arrays of micro-measurements. Our approach generalizes that of Chalupka et al. (2015) to the setting in which the macro-level effect is not specified. We formalize the connection between micro- and macro-variables in such situations and provide a coherent framework describing causal relations at multiple levels of analysis. We present an algorithm that discovers macro-variable causes and effects from micro-level measurements obtained from an experiment. We further show how to design experiments to discover macro-variables from observational micro-variable data. Finally, we show that under specific conditions, one can identify multiple levels of causal structure. Throughout the article, we use a simulated neuroscience multi-unit recording experiment to illustrate the ideas and the algorithms.

Visual Causal Feature Learning

We provide a rigorous definition of the visual cause of a behavior that is broadly applicable to the visually driven behavior in humans, animals, neurons, robots and other perceiving systems. Our framework generalizes standard accounts of causal learning to settings in which the causal variables need to be constructed from micro-variables. We prove the Causal Coarsening Theorem, which allows us to gain causal knowledge from observational data with minimal experimental effort. The theorem provides a connection to standard inference techniques in machine learning that identify features of an image that correlate with, but may not cause, the target behavior. Finally, we propose an active learning scheme to learn a manipulator function that performs optimal manipulations on the image to automatically identify the visual cause of a target behavior. We illustrate our inference and learning algorithms in experiments based on both synthetic and real data.

Discovering Cyclic Causal Models with Latent Variables: A General SAT-Based Procedure

We present a very general approach to learning the structure of causal models based on d-separation constraints, obtained from any given set of overlapping passive observational or experimental data sets. The procedure allows for both directed cycles (feedback loops) and the presence of latent variables. Our approach is based on a logical representation of causal pathways, which permits the integration of quite general background knowledge, and inference is performed using a Boolean satisfiability (SAT) solver. The procedure is complete in that it exhausts the available information on whether any given edge can be determined to be present or absent, and returns "unknown" otherwise. Many existing constraint-based causal discovery algorithms can be seen as special cases, tailored to circumstances in which one or more restricting assumptions apply. Simulations illustrate the effect of these assumptions on discovery and how the present algorithm scales.