Non-rigid Motion Correction for MRI Reconstruction via Coarse-To-Fine Diffusion Models

Magnetic Resonance Imaging (MRI) is highly susceptible to motion artifacts due to the extended acquisition times required for k-space sampling. These artifacts can compromise diagnostic utility, particularly for dynamic imaging. We propose a novel alternating minimization framework that leverages a bespoke diffusion model to jointly reconstruct and correct non-rigid motion-corrupted k-space data. The diffusion model uses a coarse-to-fine denoising strategy to capture large overall motion and reconstruct the lower frequencies of the image first, providing a better inductive bias for motion estimation than that of standard diffusion models. We demonstrate the performance of our approach on both real-world cine cardiac MRI datasets and complex simulated rigid and non-rigid deformations, even when each motion state is undersampled by a factor of 64x. Additionally, our method is agnostic to sampling patterns, anatomical variations, and MRI scanning protocols, as long as some low frequency components are sampled during each motion state.

K-band: Self-supervised MRI Reconstruction via Stochastic Gradient Descent over K-space Subsets

Although deep learning (DL) methods are powerful for solving inverse problems, their reliance on high-quality training data is a major hurdle. This is significant in high-dimensional (dynamic/volumetric) magnetic resonance imaging (MRI), where acquisition of high-resolution fully sampled k-space data is impractical. We introduce a novel mathematical framework, dubbed k-band, that enables training DL models using only partial, limited-resolution k-space data. Specifically, we introduce training with stochastic gradient descent (SGD) over k-space subsets. In each training iteration, rather than using the fully sampled k-space for computing gradients, we use only a small k-space portion. This concept is compatible with different sampling strategies; here we demonstrate the method for k-space "bands", which have limited resolution in one dimension and can hence be acquired rapidly. We prove analytically that our method stochastically approximates the gradients computed in a fully-supervised setup, when two simple conditions are met: (i) the limited-resolution axis is chosen randomly-uniformly for every new scan, hence k-space is fully covered across the entire training set, and (ii) the loss function is weighed with a mask, derived here analytically, which facilitates accurate reconstruction of high-resolution details. Numerical experiments with raw MRI data indicate that k-band outperforms two other methods trained on limited-resolution data and performs comparably to state-of-the-art (SoTA) methods trained on high-resolution data. k-band hence obtains SoTA performance, with the advantage of training using only limited-resolution data. This work hence introduces a practical, easy-to-implement, self-supervised training framework, which involves fast acquisition and self-supervised reconstruction and offers theoretical guarantees.

pyBKT: An Accessible Python Library of Bayesian Knowledge Tracing Models

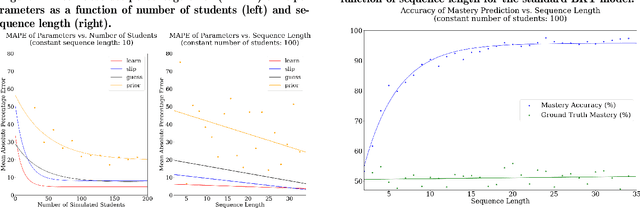
Bayesian Knowledge Tracing, a model used for cognitive mastery estimation, has been a hallmark of adaptive learning research and an integral component of deployed intelligent tutoring systems (ITS). In this paper, we provide a brief history of knowledge tracing model research and introduce pyBKT, an accessible and computationally efficient library of model extensions from the literature. The library provides data generation, fitting, prediction, and cross-validation routines, as well as a simple to use data helper interface to ingest typical tutor log dataset formats. We evaluate the runtime with various dataset sizes and compare to past implementations. Additionally, we conduct sanity checks of the model using experiments with simulated data to evaluate the accuracy of its EM parameter learning and use real-world data to validate its predictions, comparing pyBKT's supported model variants with results from the papers in which they were originally introduced. The library is open source and open license for the purpose of making knowledge tracing more accessible to communities of research and practice and to facilitate progress in the field through easier replication of past approaches.