Survival Multiarmed Bandits with Boostrapping Methods

The Multiarmed Bandits (MAB) problem has been extensively studied and has seen many practical applications in a variety of fields. The Survival Multiarmed Bandits (S-MAB) open problem is an extension which constrains an agent to a budget that is directly related to observed rewards. As budget depletion leads to ruin, an agent's objective is to both maximize expected cumulative rewards and minimize the probability of ruin. This paper presents a framework that addresses such dual goal using an objective function balanced by a ruin aversion component. Action values are estimated through a novel approach which consists of bootstrapping samples from previously observed rewards. In numerical experiments, the policies we present outperform benchmarks from the literature.

Enhancing Deep Hedging of Options with Implied Volatility Surface Feedback Information

We present a dynamic hedging scheme for S&P 500 options, where rebalancing decisions are enhanced by integrating information about the implied volatility surface dynamics. The optimal hedging strategy is obtained through a deep policy gradient-type reinforcement learning algorithm, with a novel hybrid neural network architecture improving the training performance. The favorable inclusion of forward-looking information embedded in the volatility surface allows our procedure to outperform several conventional benchmarks such as practitioner and smiled-implied delta hedging procedures, both in simulation and backtesting experiments.

Catastrophic-risk-aware reinforcement learning with extreme-value-theory-based policy gradients

This paper tackles the problem of mitigating catastrophic risk (which is risk with very low frequency but very high severity) in the context of a sequential decision making process. This problem is particularly challenging due to the scarcity of observations in the far tail of the distribution of cumulative costs (negative rewards). A policy gradient algorithm is developed, that we call POTPG. It is based on approximations of the tail risk derived from extreme value theory. Numerical experiments highlight the out-performance of our method over common benchmarks, relying on the empirical distribution. An application to financial risk management, more precisely to the dynamic hedging of a financial option, is presented.

Deep Hedging with Market Impact

Dynamic hedging is the practice of periodically transacting financial instruments to offset the risk caused by an investment or a liability. Dynamic hedging optimization can be framed as a sequential decision problem; thus, Reinforcement Learning (RL) models were recently proposed to tackle this task. However, existing RL works for hedging do not consider market impact caused by the finite liquidity of traded instruments. Integrating such feature can be crucial to achieve optimal performance when hedging options on stocks with limited liquidity. In this paper, we propose a novel general market impact dynamic hedging model based on Deep Reinforcement Learning (DRL) that considers several realistic features such as convex market impacts, and impact persistence through time. The optimal policy obtained from the DRL model is analysed using several option hedging simulations and compared to commonly used procedures such as delta hedging. Results show our DRL model behaves better in contexts of low liquidity by, among others: 1) learning the extent to which portfolio rebalancing actions should be dampened or delayed to avoid high costs, 2) factoring in the impact of features not considered by conventional approaches, such as previous hedging errors through the portfolio value, and the underlying asset's drift (i.e. the magnitude of its expected return).

Linear pretraining in recurrent mixture density networks

We present a method for pretraining a recurrent mixture density network (RMDN). We also propose a slight modification to the architecture of the RMDN-GARCH proposed by Nikolaev et al. [2012]. The pretraining method helps the RMDN avoid bad local minima during training and improves its robustness to the persistent NaN problem, as defined by Guillaumes [2017], which is often encountered with mixture density networks. Such problem consists in frequently obtaining "Not a number" (NaN) values during training. The pretraining method proposed resolves these issues by training the linear nodes in the hidden layer of the RMDN before starting including non-linear node updates. Such an approach improves the performance of the RMDN and ensures it surpasses that of the GARCH model, which is the RMDN's linear counterpart.

Risk averse non-stationary multi-armed bandits

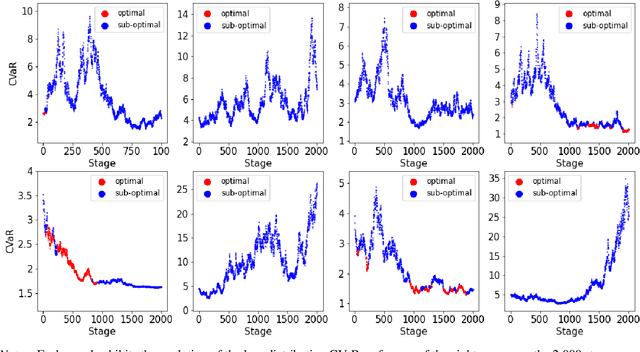
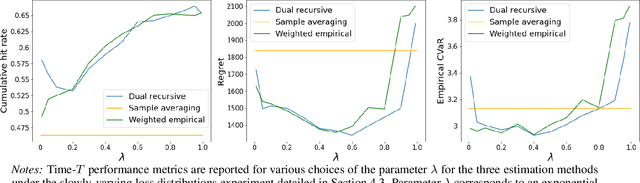
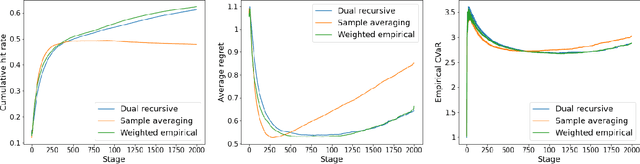
This paper tackles the risk averse multi-armed bandits problem when incurred losses are non-stationary. The conditional value-at-risk (CVaR) is used as the objective function. Two estimation methods are proposed for this objective function in the presence of non-stationary losses, one relying on a weighted empirical distribution of losses and another on the dual representation of the CVaR. Such estimates can then be embedded into classic arm selection methods such as epsilon-greedy policies. Simulation experiments assess the performance of the arm selection algorithms based on the two novel estimation approaches, and such policies are shown to outperform naive benchmarks not taking non-stationarity into account.

Bias-Corrected Peaks-Over-Threshold Estimation of the CVaR

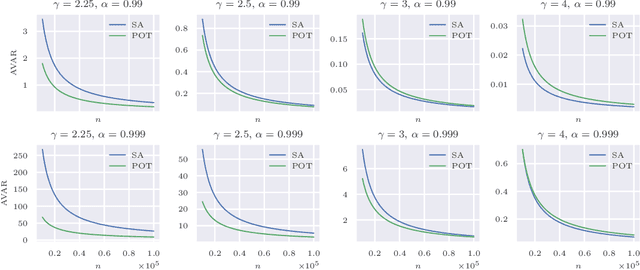
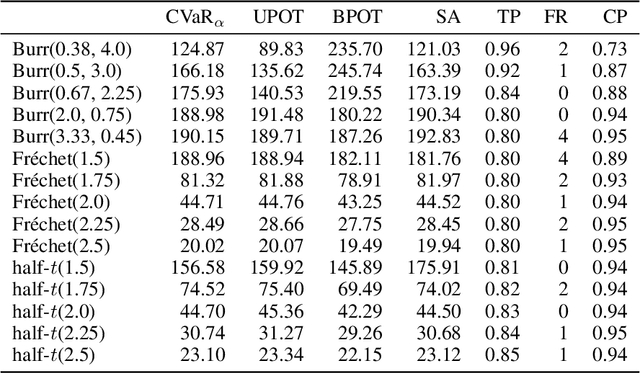
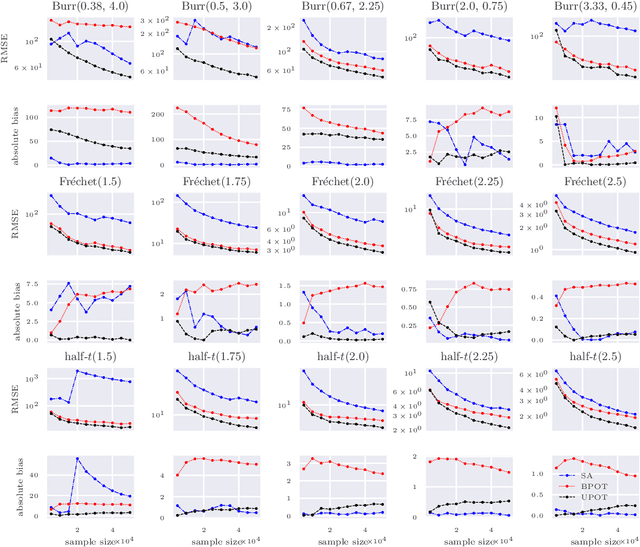
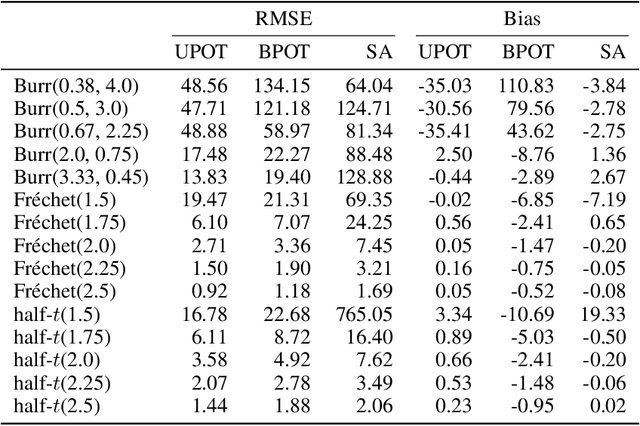
The conditional value-at-risk (CVaR) is a useful risk measure in fields such as machine learning, finance, insurance, energy, etc. When measuring very extreme risk, the commonly used CVaR estimation method of sample averaging does not work well due to limited data above the value-at-risk (VaR), the quantile corresponding to the CVaR level. To mitigate this problem, the CVaR can be estimated by extrapolating above a lower threshold than the VaR using a generalized Pareto distribution (GPD), which is often referred to as the peaks-over-threshold (POT) approach. This method often requires a very high threshold to fit well, leading to high variance in estimation, and can induce significant bias if the threshold is chosen too low. In this paper, we derive a new expression for the GPD approximation error of the CVaR, a bias term induced by the choice of threshold, as well as a bias correction method for the estimated GPD parameters. This leads to the derivation of a new estimator for the CVaR that we prove to be asymptotically unbiased. In a practical setting, we show through experiments that our estimator provides a significant performance improvement compared with competing CVaR estimators in finite samples. As a consequence of our bias correction method, it is also shown that a much lower threshold can be selected without introducing significant bias. This allows a larger portion of data to be be used in CVaR estimation compared with the typical POT approach, leading to more stable estimates. As secondary results, a new estimator for a second-order parameter of heavy-tailed distributions is derived, as well as a confidence interval for the CVaR which enables quantifying the level of variability in our estimator.

Risk-Averse Action Selection Using Extreme Value Theory Estimates of the CVaR

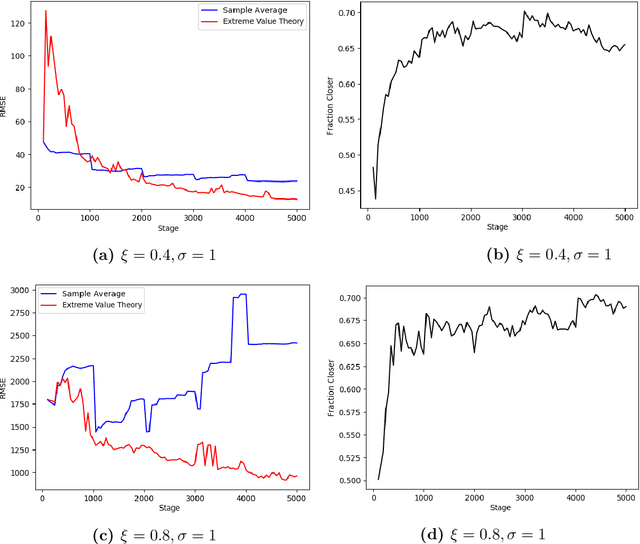
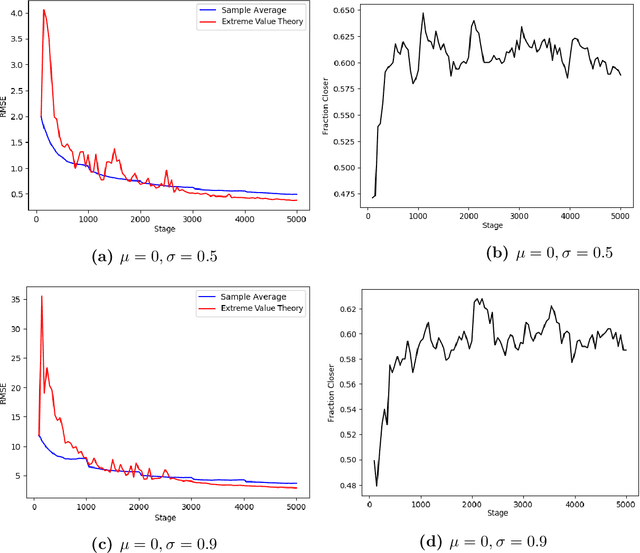
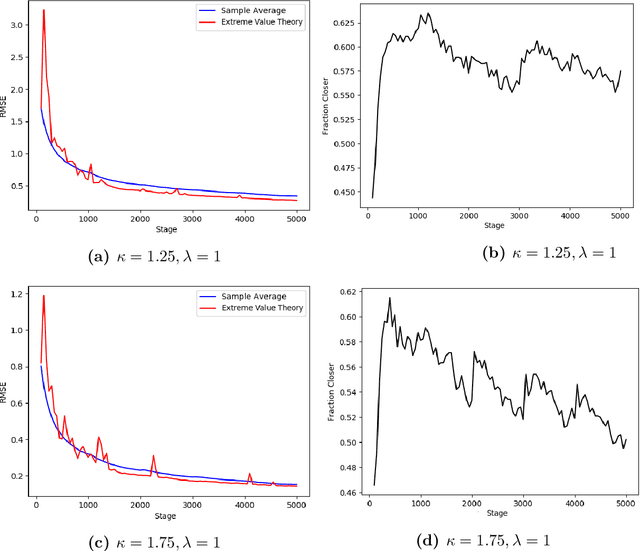
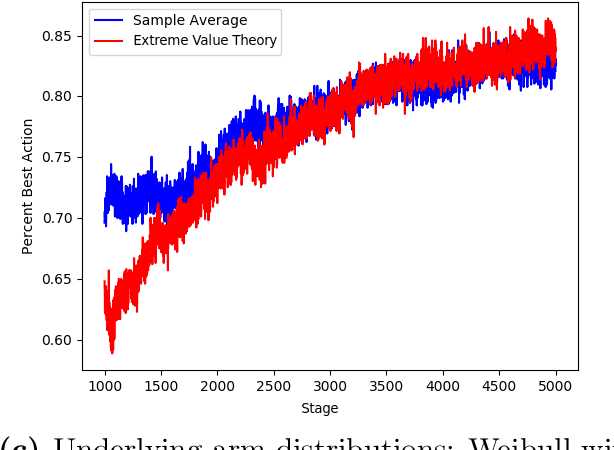
The Conditional Value-at-Risk (CVaR) is a useful risk measure in machine learning, finance, insurance, energy, etc. When the CVaR confidence parameter is very high, estimation by sample averaging exhibits high variance due to the limited number of samples above the corresponding threshold. To mitigate this problem, we present an estimation procedure for the CVaR that combines extreme value theory and a recently introduced method of automated threshold selection by Bader et al. (2018). Under appropriate conditions, we estimate the tail risk using a generalized Pareto distribution. We compare empirically this estimation procedure with the naive method of sample averaging, and show an improvement in accuracy for some specific cases. We also show how the estimation procedure can be used in reinforcement learning by applying our method to the multi-armed bandit problem where the goal is to avoid catastrophic risk.