Specification and Detection of LLM Code Smells

Large Language Models (LLMs) have gained massive popularity in recent years and are increasingly integrated into software systems for diverse purposes. However, poorly integrating them in source code may undermine software system quality. Yet, to our knowledge, there is no formal catalog of code smells specific to coding practices for LLM inference. In this paper, we introduce the concept of LLM code smells and formalize five recurrent problematic coding practices related to LLM inference in software systems, based on relevant literature. We extend the detection tool SpecDetect4AI to cover the newly defined LLM code smells and use it to validate their prevalence in a dataset of 200 open-source LLM systems. Our results show that LLM code smells affect 60.50% of the analyzed systems, with a detection precision of 86.06%.

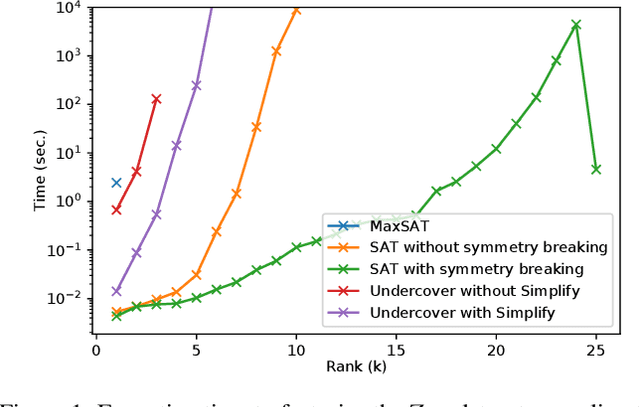
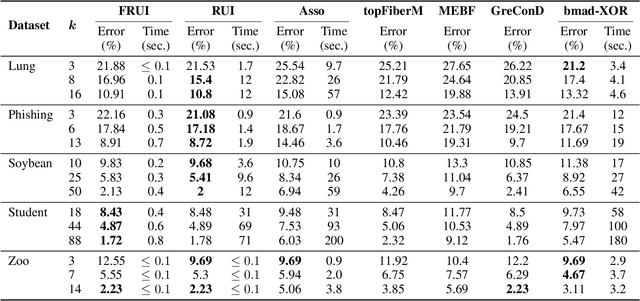
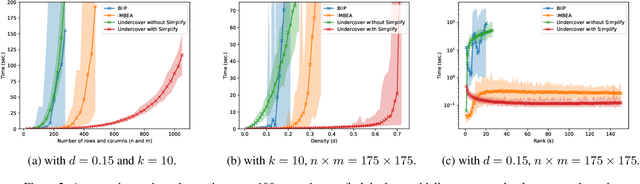
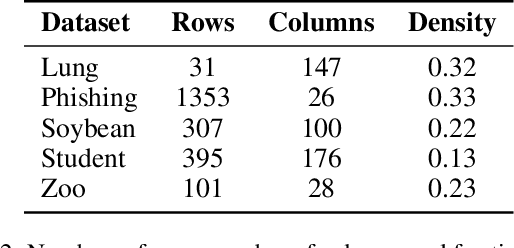
Boolean Matrix Factorization with SAT and MaxSAT

The Boolean matrix factorization problem consists in approximating a matrix by the Boolean product of two smaller Boolean matrices. To obtain optimal solutions when the matrices to be factorized are small, we propose SAT and MaxSAT encoding; however, when the matrices to be factorized are large, we propose a heuristic based on the search for maximal biclique edge cover. We experimentally demonstrate that our approaches allow a better factorization than existing approaches while keeping reasonable computation times. Our methods also allow the handling of incomplete matrices with missing entries.

An Approach to Evaluating Learning Algorithms for Decision Trees

Learning algorithms produce software models for realising critical classification tasks. Decision trees models are simpler than other models such as neural network and they are used in various critical domains such as the medical and the aeronautics. Low or unknown learning ability algorithms does not permit us to trust the produced software models, which lead to costly test activities for validating the models and to the waste of learning time in case the models are likely to be faulty due to the learning inability. Methods for evaluating the decision trees learning ability, as well as that for the other models, are needed especially since the testing of the learned models is still a hot topic. We propose a novel oracle-centered approach to evaluate (the learning ability of) learning algorithms for decision trees. It consists of generating data from reference trees playing the role of oracles, producing learned trees with existing learning algorithms, and determining the degree of correctness (DOE) of the learned trees by comparing them with the oracles. The average DOE is used to estimate the quality of the learning algorithm. the We assess five decision tree learning algorithms based on the proposed approach.

Learning Optimal Decision Trees from Large Datasets

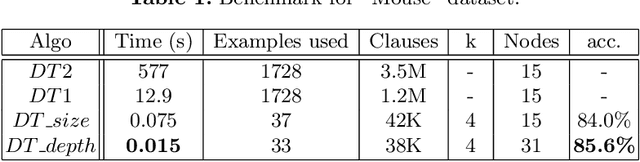
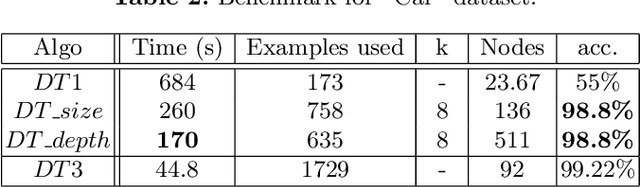
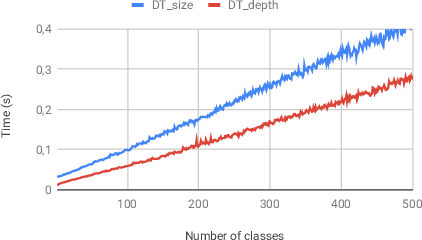
Inferring a decision tree from a given dataset is one of the classic problems in machine learning. This problem consists of buildings, from a labelled dataset, a tree such that each node corresponds to a class and a path between the tree root and a leaf corresponds to a conjunction of features to be satisfied in this class. Following the principle of parsimony, we want to infer a minimal tree consistent with the dataset. Unfortunately, inferring an optimal decision tree is known to be NP-complete for several definitions of optimality. Hence, the majority of existing approaches relies on heuristics, and as for the few exact inference approaches, they do not work on large data sets. In this paper, we propose a novel approach for inferring a decision tree of a minimum depth based on the incremental generation of Boolean formula. The experimental results indicate that it scales sufficiently well and the time it takes to run grows slowly with the size of dataset.