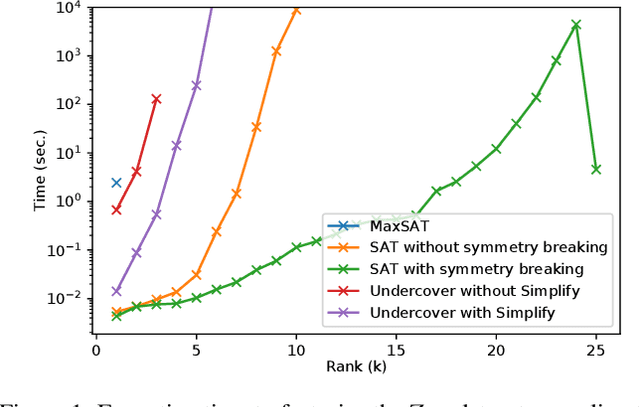
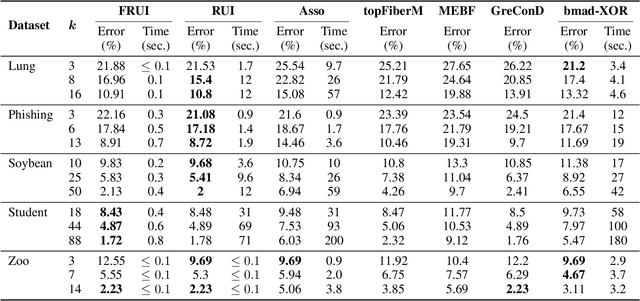
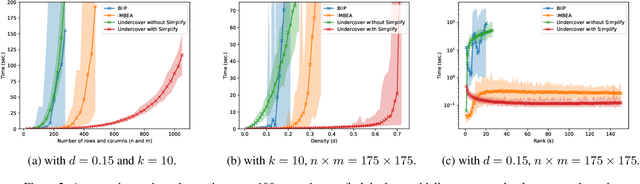
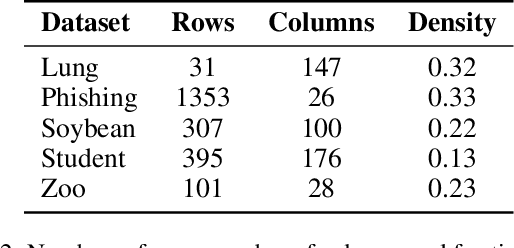
Boolean Matrix Factorization with SAT and MaxSAT

The Boolean matrix factorization problem consists in approximating a matrix by the Boolean product of two smaller Boolean matrices. To obtain optimal solutions when the matrices to be factorized are small, we propose SAT and MaxSAT encoding; however, when the matrices to be factorized are large, we propose a heuristic based on the search for maximal biclique edge cover. We experimentally demonstrate that our approaches allow a better factorization than existing approaches while keeping reasonable computation times. Our methods also allow the handling of incomplete matrices with missing entries.

Efficient Partial Order CDCL Using Assertion Level Choice Heuristics

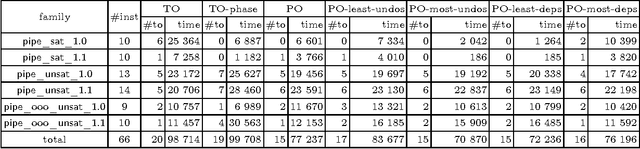
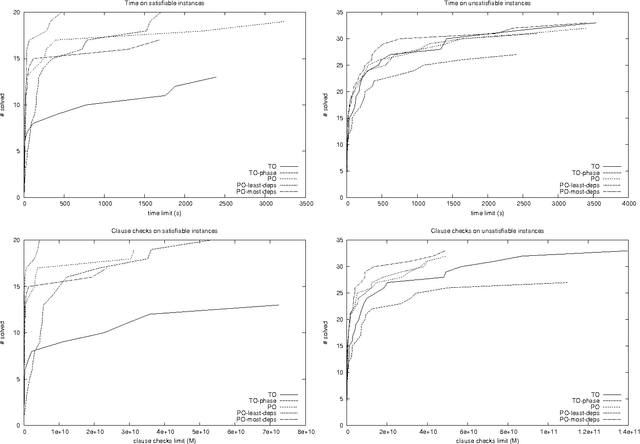
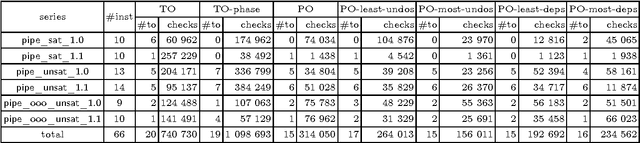
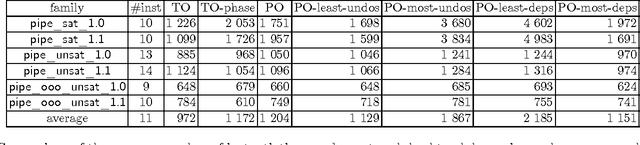
We previously designed Partial Order Conflict Driven Clause Learning (PO-CDCL), a variation of the satisfiability solving CDCL algorithm with a partial order on decision levels, and showed that it can speed up the solving on problems with a high independence between decision levels. In this paper, we more thoroughly analyze the reasons of the efficiency of PO-CDCL. Of particular importance is that the partial order introduces several candidates for the assertion level. By evaluating different heuristics for this choice, we show that the assertion level selection has an important impact on solving and that a carefully designed heuristic can significantly improve performances on relevant benchmarks.